高速场景下基于OFDM 的信道估计算法

马宏彪，徐 岩

（兰州交通大学 电子与信息工程学院，甘肃 兰州 730070）

0 引 言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）系统具有良好的频谱利用率、较高的传输速率和抗多径干扰能力[1]，已经在多种无线通信标准中得到广泛的应用，并且也是5G 多载波传输技术的基础。随着我国高速铁路网的日益密集，人们对高速移动场景下通信质量的需求日益增强。在高速场景下，无线信道出现时间和频率的严重扩展，此时信道呈现出的快时变特性给高速铁路通信系统带来了严峻的挑战[2]。OFDM 系统的信道响应在多个符号甚至一个符号上发生变化，需要耗费大量的频率或时间资源估计信道状态信息（Channel State Information，CSI），另一方面，多普勒频移引起的载波频偏导致载波间干扰（Inter⁃Carrier Interference，ICI）的产生，影响估计精度，导致接收端性能下降。这两个主要问题决定了高速场景下通信链路的性能。如何准确获取CSI 和抑制ICI 是高移动性通信系统面临的重要问题[3⁃4]，信道估计作为接收端的关键环节，其重要性更加凸显。

目前针对时变信道模型的研究主要分为线性时变模型和基扩展模型[5]（Basis Expansion Model，BEM）。其中，线性时变模型将信道变化视为简单的线性变化过程，适用于多普勒频移较小的场景。BEM 通过选取适当的正交基函数拟合信道状态，相较线性时变模型更加准确。采用BEM 对时变信道建模是把一个OFDM 符号内的信道信息用少量BEM 函数表示[6]，这样可以简化时变信道的待估参数。文献[7⁃9]基于OFDM 系统研究了不同类型BEM 的时变信道建模方法，此类方法可以有效拟合高速场景下的时变信道。OFDM 系统在时变信道估计中通常采用导频辅助的方法，对导频数据最常用的算法是最小二乘（Least Square，LS）算法，其结构简单，但易受信道状态影响。基于DFT 的信道估计算法易于实现，受到广泛关注，文献[10]针对LS 算法的不足，提出阈值DFT 的改进算法，对信道频率响应中的噪声进行抑制以提高估计精度。文献[11]提出一种低复杂度的卡尔曼滤波（Kalman Filtering，KF）方法，采用KF 技术进行子空间跟踪，建立状态方程和测量方程，可以有效跟踪时变信道。

本文分析了OFDM 系统在时变信道下的传播特性，采用BEM 进行信道建模，然后用KF 技术对导频处的信道冲激响应进行估计，同时采用组导频图样抑制ICI。通过仿真结果分析验证本文算法可以有效提升估计精度，降低系统误码率。

1 时变信道模型

1.1 OFDM 系统模型

如图1 所示，OFDM 通信系统包含发送端和接收端两个部分。根据图1 中的系统模型框图可以对OFDM系统的信号传输过程建立如下的数学表示：在发送端假设传送符号中的子载波总数为N，插入导频后表示为X(k)。经过IDFT 得到时域信号x(n)：

式中k=0,1,2,…,N-1。

图1 OFDM 通信系统模型

发送端在经过串并转换后插入循环前缀（Cyclic Prefix，CP）可以消除符号间干扰[12]（Inter⁃Symbol Interfe⁃rence，ISI）。信号经过时变信道，在接收端去除CP 得到接收信号y(n)，可以表示为：

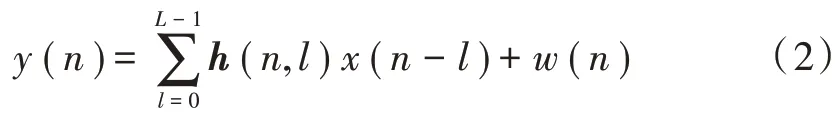
式中：n=0,1,2,…,N-1；L表示多径数目；w(n)表示高斯白噪声。

y(n)经过 DFT 变换得到信号Y(k)：

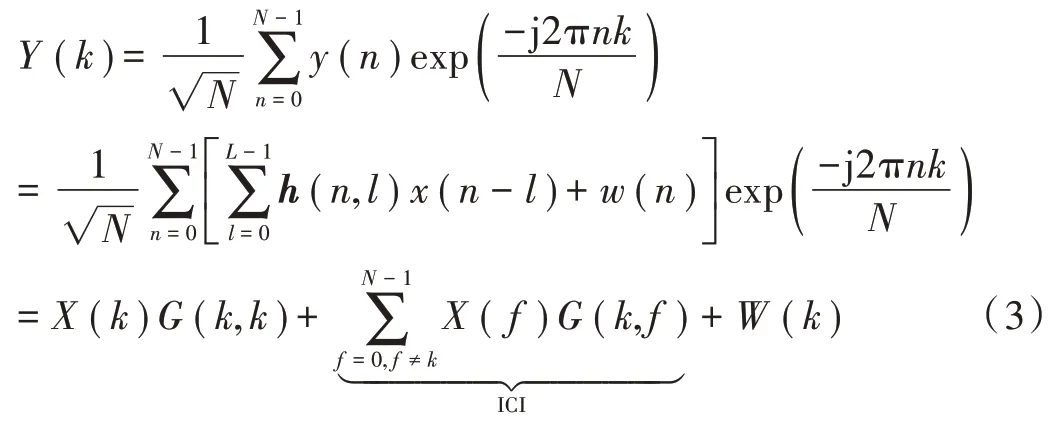
式中W(k)是w(n)的傅里叶变换。

高速移动场景下OFDM 符号周期内的信道冲激响应是时变的，各子载波受时变信道影响不再保持正交。式（3）显示接收信号中每个载波上的信息不仅包含可用信号，还包括相邻的载波受时变信道影响对当前载波产生的干扰，即ICI 部分。在高速移动环境下由于多普勒频移的影响，ICI 增强导致信道估计算法的精度受到影响，进而影响整个通信系统的性能。

1.2 基于BEM 的时变信道建模

BEM 建模的原理是使用一组相互正交的基函数与其相应系数的乘积来拟合时变信道。由于BEM 基函数是已知的一组固定的正交基，那么采用估计算法得到BEM 系数后再经过BEM 模型即可得到信道响应。

BEM 的一般表达式为：

式中：n=0,1,2,…,N-1；l=0,1,…,L-1；bq为基函数；gq为 BEM 系数；Q为维数，通常取为最大多普勒频移，Ts为采样间隔。

式（4）的矩阵形式表示为：

式 中 ：h表 示 信 道 矩 阵 ；bq=[bq(0),bq(1),bq(2),…,bq(N-1)]T；Gq是N×N维的 Toeplitz 循环矩阵。

使用BEM 进行时变信道建模的关键在于不同基函数的选择问题，各种基扩展模型各有优势，适合不同的场景。其中，CE⁃BEM 具有基函数生成简单不依赖信道统计信息的特点[13]，因此选择CE⁃BEM 进行后续的时变信道建模。CE⁃BEM 的基函数表示为：

将式（2）改写成矩阵形式：

将相应的频域接收信号写成矩阵形式：

将式（5）代入式（8）后可表示为：

式中：FL是多径位置对应的参数矩阵，由N F响应的列组成；Gq=(gq(0),gq(1),gq(2),…,gq(L-1))T。

可以令A=Fdiag (bq)FH，则式（9）表示为：

此时对信道矩阵H的估计就转化为对BEM 系数g的估计，利用在发送端插入的导频信息，使用估计算法估计出 (Q+1)L个g的值。

2 时变信道估计

2.1 导频图样

时变信道下OFDM 系统的信道估计通常采用导频辅助的方法，受时变信道的影响，相邻载波信号会对导频处信号产生影响，为了抑制ICI，这里采用组导频[14]。如图2 所示，组导频图样在频域方向将m个长度为1+2D的组导频插入OFDM 符号中，可以记为组导频图样是在传统梳状导频基础上，在当前导频左右两侧分别加入长度为D的相同导频，作为保护导频。如之前分析，当前子载波受相邻载波影响，距离越近影响越强，在导频两侧加入保护导频，可以有效降低干扰。

图2 导频组图样

接收端第m个导频组的输出表示为：

将式（11）改写为：

从当前公共实训基地的发展实际看，一方面资源投入不足，办学整体条件较差，公共服务能力不高；另一方面存量资源配置不合理，布局离散，低水平重复建设严重。因此，必须树立共建共享共赢的理念，充分发挥政府、学校、社会、企业、个人多个积极性，通过政府主导、校企合作、校际联合等途径，采取“合并、共建、联办、划转”等形式，进行资源重组，改变分散办学、重复办学、资源配置不合理、办学效益低的状况，齐心协力推动实训基地可持续发展。

进一步将OFDM 符号内的所有导频数据一起考虑 。 即 令且W(p)=那么可以得到：

2.2 基于KF 的时变信道估计

在建立基于BEM 的时变信道模型后，重点在BEM系数g的估计。最常用的算法是LS 算法，该算法通过代价函数最小，求解估计值。解得LS 算法的估计值为：

LS 算法结构简单、应用广泛，但其估计过程忽略了噪声的影响，因而估计误差较大，特别是在时变信道或者信噪比较差的环境中。此外，传统信道估计算法将每个OFDM 符号当作单独的个体而忽略了相邻符号之间的相关性，换言之，相邻符号对应的参数之间是随着时间平滑演变的。

KF 技术用状态方程表示信道变化，是一个递归计算的过程，非常适合时变信道估计[15]。在BEM 信道建模基础上可以构建状态空间模型，利用KF 技术估计信道冲击响应。考虑复杂度的问题，这里采用一阶自回归（AR）模型表示：

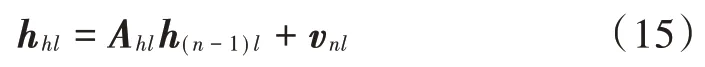
式中：hnl是第n个OFDM 符号块第l条路径的信道响应向量；Ahl是信道系数状态转移矩阵；vnl是模型的误差。

进一步，可以将BEM 代入hnl：

式中：hnl=(hn(0,l),hn(1,l),…,hn(N-1,l))T；B=(b0,b1,b2,…,bQ) 是 BEM 基 函 数 矩 阵 ；gnl=(g0(l),g1(l),g2(l),…,gQ(l))T是基系数矩阵。

由于BEM 基函数是确定的，并且其系数为自相关的高斯变量[16]，那么可以建立关于BEM 系数的AR 模型来表示g的动态关系，如下：

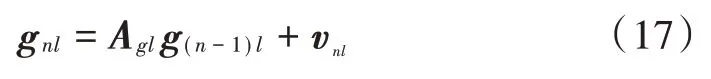
式中：Agl为BEM 系数状态转移矩阵；vnl是模型的误差。

AR 模型的参数可以由尤尓⁃沃克（Yule⁃Walker）方程[6]得到：

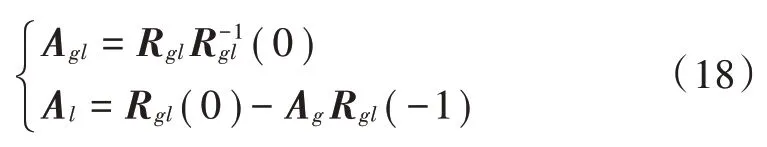
由于BEM 基函数系数是均值为零的相关复高斯变量，则相关矩阵为：

式中s为相关位移。

那么状态转移方程表示为：

测量方程为：

基于KF 技术的信道估计步骤如下：

1）状态初始化

2）时间方程更新

3）测量方程更新

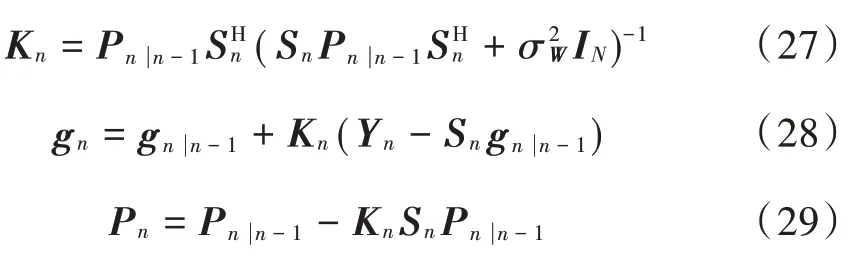
式中：gn|n-1为预估计值；gn为估计值；Pn为协方差估计矩阵；Pn|n-1是预估计误差矩阵是噪声方差；IN是单位方阵。

3 仿真分析

在仿真实验中，通过Jakes 模型[7]模拟时变信道场景，接收端以一定速度运行，发送端信号经过不同路径到达接收端，通过Matlab 对4 种算法在时变信道下进行仿真。仿真中系统的具体参数设置如表1 所示。为了验证本文算法的有效性，在仿真实验中通过设置移动端不同的运行速度对比了传统LS 算法、文献[10]中提出的基于LS 的阈值DFT 算法、基于BEM 的LS 算法和本文算法。采用信噪比（Signal Noise Ratio，SNR）作为接收端性能表现的评价指标。

表1 仿真系统参数

图3～图5 中通过设置移动端运行速度为50 km/h，200 km/h，350 km/h，展现在不同信噪比条件下系统误码率变化的趋势。从中可以看出，传统的LS 算法在计算过程中由于忽略噪声等影响因素，性能表现最差。文献[10]针对LS 算法的不足，通过设置阈值，对估计结果进行判决去噪，可以看出此算法在50 km/h 这样的低速环境下对LS 算法有一定提升，但是随着移动端速度增加，多普勒效应增强，此算法性能提升有限。BEM⁃LS算法是在BEM 建模的基础上采用LS 算法对时变信道进行估计，估计性能相较于传统的LS 算法有一定提升，说明通过BEM 建模可以提升传统估计算法的估计精度。但随着移动端速度的增加，ICI 增强，前3 种算法没有对ICI 抑制的措施，OFDM 系统的估计精度受到影响。如图4，图5 所示，当移动端速度达到200 km/h 和350 km/h时，前3 种算法都出现了误码平底现象，而本文算法是在BEM 建模的基础上，采用KF 技术通过预测⁃更新可以对信道进行实时追踪，并且采用组导频图样抑制ICI 的影响。从图中可以看出此算法相较于其他算法在各种速度条件下都有明显的优势。

从图3 可以看出，当移动端运行速度较低时，随着信噪比条件变化，4 种算法的BER 性能呈现变好的趋势。在系统BER 为10-2时，本文算法相较于其他算法有3～7 dB 的性能增益。当移动端运行速度为200 km/h，如图4 所示，系统BER 为10-1时，本文算法相较于其他算法有2.5～6 dB 的性能增益。如图5 所示，当移动速度达到350 km/h 时，4 种算法由于受到ICI 的影响，估计精度下降，此时本文算法依然优于其他算法。

图3 移动端速度为50 km/h 时4 种算法的BER

图4 移动端速度为200 km/h 时4 种算法的BER

图5 移动端速度为350 km/h 时4 种算法的BER

在图6 的仿真中，设置SNR=15 dB，移动端速度变化范围为100～350 km/h。展现了传统LS 算法、文献[10]阈值DFT 算法、BEM⁃LS 和本文算法在连续速度变化下的误码率性能表现。从图6 中可以看出，随着移动端速度增加，ICI 对4 种算法的误码率性能都带来了影响，本文算法误码率性能明显优于其他3 种算法。因为本文算法一方面采用KF 技术对时变信道进行有效追踪，另一方面采用组导频组图样对ICI 起到抑制作用，可以有效地提升估计精度。

图6 SNR 为15 dB 时4 种算法在不同速度下的BER

4 结 语

为了解决OFDM 系统在高速移动场景下的信道估计问题，提出一种基于基扩展模型的信道估计算法。采用BEM 拟合时变信道，将对时变信道的估计转化为基函数系数的估计。采用组导频对ICI 进行抑制；使用KF技术通过预测⁃更新对信道进行实时追踪。通过仿真对比了本文提出的信道估计算法与几种传统的信道估计算法在不同条件环境下的信道估计性能。结果显示，本文提出的算法在高速场景下，性能指标具有明显的优势，能够保证高速场景下的链路性能。