相干多径环境下的毫米波大规模MIMO混合波束赋形方案

周 围，彭 洋，冉靖萱，陈星宇，马茂琼

(1.重庆邮电大学 光电工程学院，重庆 400065；2.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

0 引 言

大规模多输入多输出(multiple input multiple output, MIMO)系统和毫米波技术的结合，提高了频谱效率，克服了带宽限制[1]，被视为5G的核心技术。传统MIMO系统采用纯数字波束赋形(digital beamforming, DBF)，可使电磁波按特定的方向传输，从而大大提升信干噪比[2]，但要求为每根天线配置一条射频(radio frequency, RF)链。大规模MIMO中天线阵元数量庞大，采用纯数字波束赋形的成本太高[3]，因此，基于减少RF链的混合波束赋形(hybrid beamforming, HBF)技术，可降低成本和功耗，成为近年来研究的热点之一。

在通信系统中，尤其在密集城区，常存在严重的多径效应，导致信号严重衰落，特别是在相干多径的情况下，信源相关矩阵亏秩，导致矩阵奇异，此时，传统的波束赋形算法均会失效[4]。通常采用空间平滑技术对相干源进行预处理，但传统的解相干技术很难直接用于混合波束赋形系统，且目前对于混合波束赋形中结合传统解相干技术的研究非常少。文献[5]为减少射频链的数量和基带能量消耗，提出了一种节能算法来评估射频链的最优数目，实现了硬件成本和能量效率的有效权衡；文献[6]在毫米波大规模MIMO系统的上行和下行都采用全连接混合波束赋形，结果表明，在使用较少的RF链时，混合波束赋形方案几乎达到纯数字波束赋形的性能；文献[7]研究了一种实用的多用户大规模MIMO混合波束赋形系统：在模拟域进行波束选择，在数字域采用迫零(zero forcing, ZF)预编码；文献[8]在多用户毫米波大规模 MIMO系统的下行链路，设计混合波束赋形来优化能源效率；文献[9]介绍了经典的正交匹配追踪(orthogonal matching pursuit, OMP)算法，在此基础上提出基于施密特正交化的混合波束赋形(gram-Schmidt HBF, GS-HBF)算法，通过正交化模拟波束赋形矩阵，可避免矩阵求逆，降低了系统复杂度；文献[10]提出了一种迭代波束赋形方案，在阵元数较多时，不同的毫米波信道路径近似正交，通过在收发端阵列不断对信号进行迭代收发，从而获取最大增益的路径，对应的阵列响应作为波束成形向量，但该方案无法有效抑制干扰方向上的信号。可以看出，目前的混合波束赋形大多是针对其能耗、频谱效率等性能进行优化，而并未直接关注相干多径信号对目标信号的影响，且多数算法是需要利用信道的奇异值分解(singular value decomposition, SVD)预先获得最优的无约束波束赋形矩阵，再分别求得模拟和数字波束赋形矩阵，复杂度较高，步骤冗余。

针对上述问题，本文提出相干多径环境下的混合波束赋形方案，结合波束扫描、信号重构和解相干算法，解决了混合波束赋形无法直接使用传统解相干算法的问题，且无需预先求解最优无约束波束赋形矩阵。所提方案可将主波束对准目标信号方向，并在相干和非相干干扰信号方向形成较深的“零陷”，因此，可以获得良好的信干噪比(signal to interference plus noise ratio, SINR)和频谱效率(spectral efficiency, SE)，且性能几乎逼近于纯数字波束赋形。

1 系统模型

设大规模MIMO基站为K个用户提供服务，基站端设置M个接收天线。

1.1 信号模型

对于M元均匀直线阵，其阵列响应表达式为

a(θi)=[1,e-j2π·d·sin(θi)/λ,…,e-j2π(M-1)·d·sin(θi)/λ]T

(1)

(1)式中：M为天线阵元数量；d为阵元间距；λ为波长；θi为方位角，i=1,2,…,K。

阵列接收信号的基带模型为

x(n)=[a(θ1),a(θ2),…,a(θK)]s(n)+n(n)

(2)

(2)式中：x(n)=[x1(n),x2(n),…,xM(n)]T为阵列接收信号矢量；s(n)=[s1(n),s2(n),…,sK(n)]T为信号矢量；n(n)=[n1(n),n2(n),…,nM(n)]T，其中，任意ni(n)为第i个阵元上的加性高斯白噪声，i=1,2,…,M。

1.2 阵列连接方式

混合波束赋形器按照RF链与天线的连接方式可分为全连接型和部分连接型结构，本文因为方案的理论需要，采用全连接型结构，如图1所示。

从图1可以看出，每条RF链通过移相器与全部阵元连接(需要MNRF个移相器，其中，NRF为RF链数量，且NRF≤K≪M)，FABF为模拟波束赋形矩阵，由移相器网络构成。接收信号经过模拟波束赋形后，通过RF链进入数字域，权矢量wDBF对数字信号进行数字波束赋形，最终得到输出y(n)。尽管全连接结构RF链数量限制在了用户数量以内，但每条RF链与所有的天线相连，因此，可以形成更窄的波束，获得更高的天线增益。

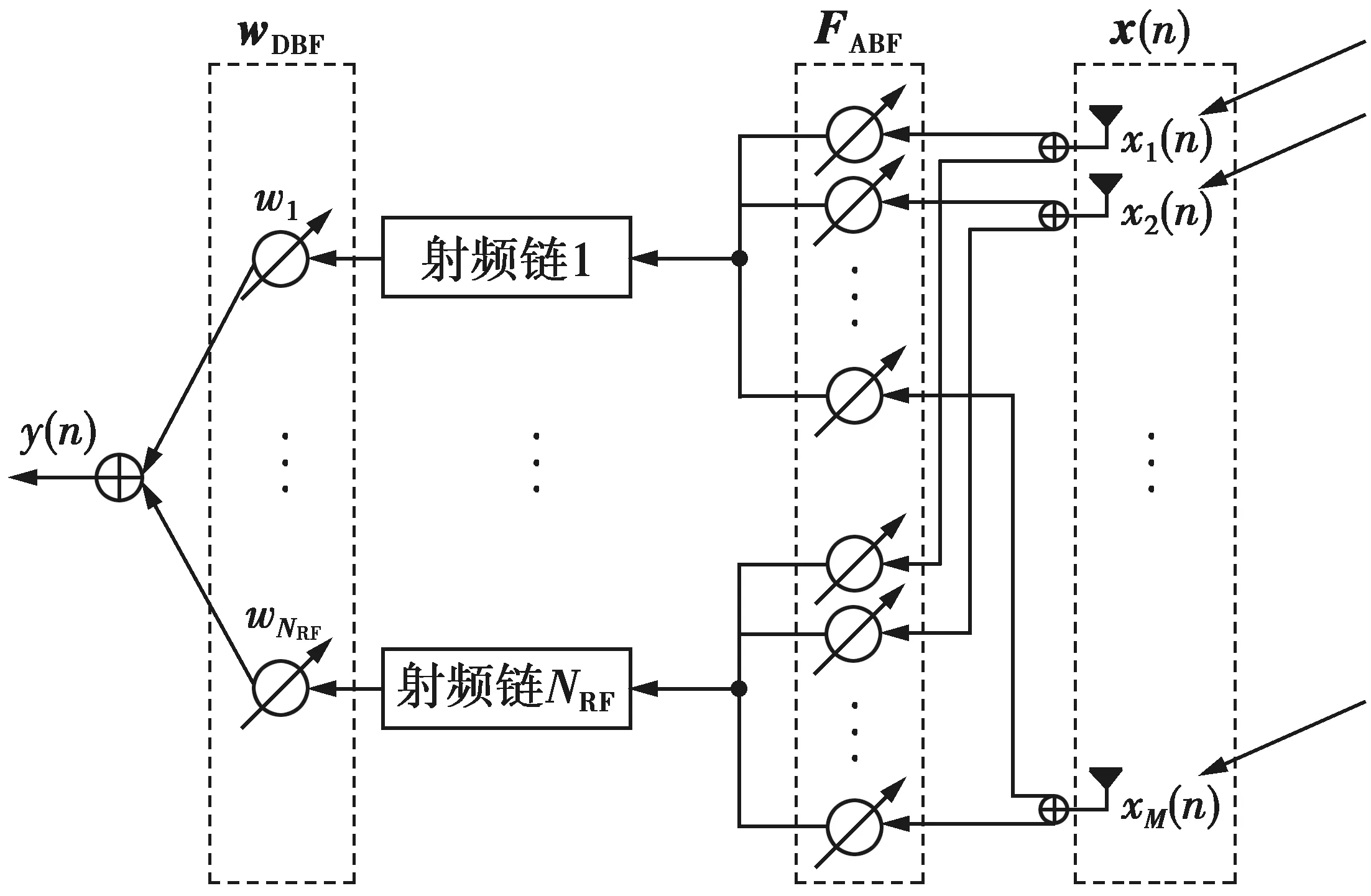
图1 混合波束赋形的全连接结构

2 混合波束赋形下的解相干方案

传统的解相干技术有均匀空间平滑技术、加权空间平滑技术等，但都是在纯数字域内进行操作，因此，不能直接应用于混合波束赋形的场景中。又由于传统混合波束赋形中，为降低成本和功耗而减少RF链，使得数字波束赋形器的维度降低，进而导致系统性能降低。本文设计了一种将数字域划分为两级的混合波束赋形方案，使得系统可以采用传统的解相干技术。本方案通过以下3个阶段进行。

2.1 模拟波束赋形

模拟波束赋形器由移相器网络构成，通过调整每个移相器的相位值，即可在模拟域对接收信号进行不同的模拟波束赋形。首先，采用离散傅里叶变换(discrete Fourier transform，DFT)码本[11]，得到码本波束矩阵，表达式为

m=1:M;n=1:Nbeam

(3)

(3)式中：Nbeam为波束数；WABF的每列可在(-π/2,π/2)形成不同指向的波束，用于接收空域内不同方向的来波信号。

然后，采用波束扫描方法[12]，对所有方向进行扫描，得到每个信号方向对应的权矢量，用集合W表示为

W={w1,w2,…,wK}

(4)

(4)式中，wk为第k个信号对应方向的权矢量，k=1∶K。所有权矢量对应的波束指向，用集合ϑbeam表示为

ϑbeam={ϑ1,ϑ2,…,ϑK}

(5)

(5)式中，ϑk为权矢量wk对应的波束指向，k=1∶K。

最后，本文设计将波束集合W中的每个波束作为模拟波束赋形矢量对接收信号进行模拟波束赋形，得到对应的输出为

(6)

(6)式中，Sk为模拟波束赋形器对第k个信号波束赋形后的输出，并令S=[S1,S2,…,SK]T,K≤NRF。

2.2 第一级数字域的信号重构

传统纯数字波束赋形中，NBB=NRF=M，其中，NBB为数字波束赋形器的维度；而混合波束赋形中，NBB=NRF≪M。本文基于恢复数字波束赋形器维度的思路，在传统混合波束赋形方案的模拟波束赋形和数字波束赋形之间，设计了一种信号重建的方案。

本文认为，可以在数字域内构建一个“虚拟的阵列”，具体为经过2.1节的模拟波束赋形后，不同方向的信号通过不同的RF链进入数字域；由于此时的信号已变为数字信号，因此，可以按照1.1节中的阵列信号模型，对每条RF链输出的数字信号重新构建“虚拟”的阵列接收信号；结合模拟域的输出和对应波束指向，信号重建的表达式为

xrecon=a(ϑ1)S1+a(ϑ2)S2+…+a(ϑK)SK

(7)

(7)式中，xrecon=[xrecon1,xrecon2,…,xreconM]T。第一级数字域的输出作为第二级数字域(数字波束赋形阶段)的输入，其优势在于重新将数字赋形恢复到与实际阵元数量等同的维度(甚至任意维度)。

2.3 第二级数字域的数字波束赋形

以xrecon作为输入的第二级数字域，可以看作是“虚拟阵列的全数字域波束赋形”。因此，可以应用传统的解相干技术，对相干干扰进行抑制。本文采用了2种解相干技术：均匀空间平滑(uniform spatial smoothing, USS)技术、加权空间平滑(weighted spatial smoothing, WSS)技术[4]，并进行对比。

由于来波方向不同，目标信号与干扰信号的相位差在各阵元上不同，而各子阵以各自第一个阵元为基准，因此，USS技术可以使2个信号的相位关系随机化，从而使得平滑相关矩阵恢复满秩。假设子阵阵元数为Msub，子阵个数(即平滑次数)为N，有N=M-Msub+1。USS算法具体步骤如下。

算法1USS算法

其中，r为Rxreconxrecon的元素；

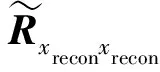
算法2WSS算法

1)全阵自相关矩阵：同算法1；

2)提取子阵的相关矩阵：同算法1；

3)构建测度函数：ξ=hTRδδh；

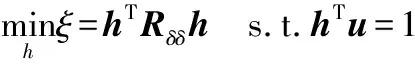
h=[h1,h2,…,hN]T

通过USS算法和WSS算法获得平滑相关矩阵后，根据线性约束最小方差(linearly constrained minimum variance, LCMV)准则，可得子阵波束赋形器的最佳权矢量wsub-opt，表达式为

(8)

为避免孔径损失，利用子阵间的相位关系，对全阵做波束赋形，表示为

wfull-opt=Twsub-opt

(9)

2.4 信干噪比和频谱效率

本文方案主要通过SINR和SE等性能进行评价。混合波束赋形后，输出信号中目标信号功率为

(10)

输出信号中干扰信号功率为

(11)

输出信号中噪声功率为

+a(ϑK)·(wKH·n)]|2

(12)

由(7)—(9)式可以得到信干噪比为

(13)

根据信干噪比，可以得到频谱效率表达式为

SE=lb|1+SINR|

(14)

3 仿真分析

为了验证所设计混合波束赋形方案的性能，本文分别从信干噪比、频谱效率等性能对其进行了仿真分析，仿真参数如表1所示。

表1 仿真参数

实验采用了蒙特卡罗的仿真方法，曲线中每一个值都是1 000次仿真的平均值。

3.1 码本设计及波束扫描仿真

本文采用DFT码本，波束数量Nbeam设置为180，根据(3)式可得到设计的码本波束集。通过波束扫描，从码本波束集中找到3个信号方向对应的波束，如图2所示。

图2 波束扫描结果

对接收信号进行模拟波束赋形，分离出不同方向的信号，并通过不同的RF链进入数字域。

3.2 波束方向分析

图3为基于LCMV准则的波束赋形方向图。可以看出，LCMV准则下的波束图在非相干干扰信号方向可形成“零陷”；但对于相干干扰信号方向，未形成“零陷”，而是与目标信号方向一样，都出现主波束，因此算法失效。

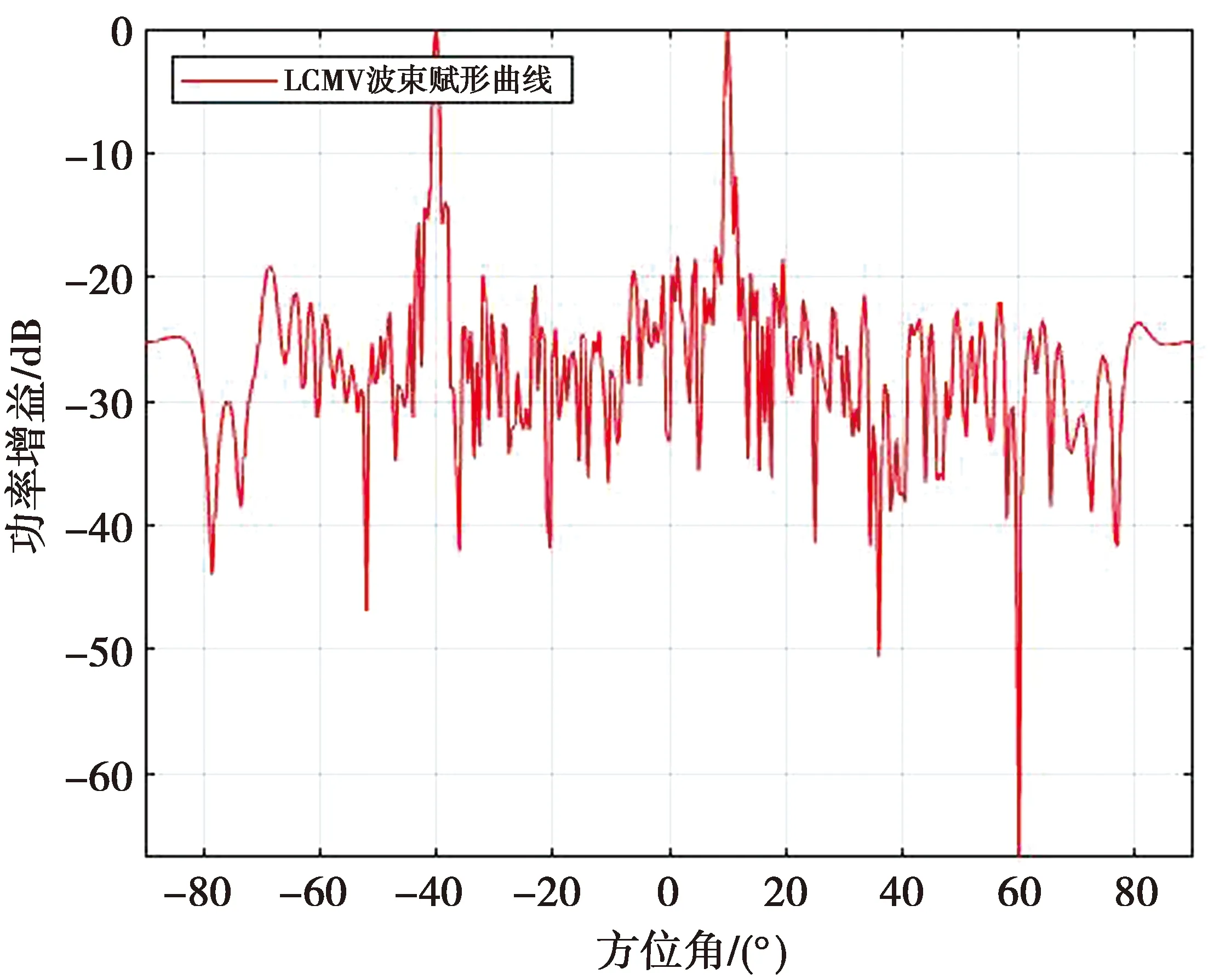
图3 LCMV波束赋形方向图(未作平滑)

图4—图6是在信噪比SNR=20 dB条件下的波束方向图。可以看出，所提出的混合波束赋形方案，使主波束对准目标方向，并且在相干干扰方向形成了较深的零陷，极大地抑制了干扰信号。图4为子阵混合波束赋形与全阵混合波束赋形的对比。可以看出，平滑处理后，相关矩阵维度降低导致孔径损失，但是全阵混合波束赋形充分利用阵列自由度，形成了更深的“零陷”，同时波瓣宽度更窄。图5为采用USS和WSS技术后的方向图对比。可以看出，WSS技术在相干干扰方向形成更深的“零陷”，这是因为WSS技术不仅解除了自相关矩阵亏秩的问题，更进一步解除了信号间的相干性。图6为混合波束赋形与纯数字波束赋形的对比。由于所提出的信号重构，使得数字域的波束赋形器的维度可以设置为与天线阵列相同的维度，因此，得到的波束方向图，无论是波瓣宽度、主波束和“零陷”的位置都几乎逼近纯数字波束赋形的方向图。

图4 基于WSS的全阵/子阵混合波束赋形方向图

图5 均匀/加权空间平滑方向图

图6 混合/纯数字波束赋形方向图

3.3 不同方案的性能对比

不同方案的信干噪比和频谱效率对比分别如图7、图8所示，包括纯数字波束赋形算法、OMP算法、GS-OMP算法以及本文方案(采用WSS技术)，RF链数为3。从图7、图8可以看出，信干噪比和频谱效率随着信噪比的增大而增大；其中，OMP算法和GS-OMP算法的性能接近，但GS-OMP算法利用施密特正交法将模拟波束赋形矩阵FRF中的阵列响应矢量两两正交化，可以避免求解数字波束赋形矩阵FBB时的矩阵求逆操作，因此，GS-OMP算法的复杂度低于OMP算法；本文所提出的混合波束赋形方案因对数字域的维度进行恢复加强了增益，所以输出信干噪比和频谱效率的性能优于其他混合波束赋形方案，且接近纯数字波束赋形的性能。

图7 信干噪比仿真图

4 结束语

传统混合波束赋形的研究无法直接应用传统解相干算法，一方面是传统混合波束赋形大多是通过对信道的SVD分解得到模拟波束赋形矩阵；另一方面是因为传统解相干算法本身是在数字域执行。本文为解决毫米波大规模MIMO系统中的相干多径问题，通过结合码本波束、信号重构，使得传统的解相干算法得以应用于混合波束赋形的场景。首先，在模拟域进行波束扫描，得到所有目标方向的码本波束并输出；然后，通过第一阶段数字域对模拟波束赋形的输出进行信号重构；最后，在第二阶段数字域执行解相干算法。仿真结果表明，混合波束赋形的主波束可以指向目标信号方向，并在相干干扰方向和非相干干扰方向均能产生较深的“零陷”；同时，在信干噪比、频谱效率等性能方面，所提出的混合波束赋形方案接近纯数字波束赋形。下一步将考虑在所提波束赋形方案基础上，研究利用现场可编程门阵列(field programmable gate array，FPGA)进行算法实现。