面向连续变量量子密钥分发的多边型LDPC码设计与性能分析

周 创，阎 昊，罗钰杰，黎 勇,3

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.西南通信研究所 保密通信重点实验室，成都 610041；3.重庆大学 计算机学院，重庆 400044)

0 引 言

连续变量量子密钥分发[1-3]系统由于量子信号本身极其微弱，而且经过长距离传输后，信噪比还会大大降低，因此，需要采用码率很低、码长很长的低密度奇偶校验(low density parity check, LDPC)码[4]。性能好的低码率码需要同时满足两个条件：一是译码阈值接近信道容量；二是最小汉明距离较大，保证误码残留很低。这给码字的设计带来了很大的挑战：一方面，为了设计低码率码且其译码阈值接近香农限，在码字结构中就需要大量度数为1的变量节点；另一方面，大量低度数的变量节点会阻碍最小汉明距离随码字长度的增加而增大。多边型LDPC码(multi-edge type LDPC, MET-LDPC)[5]码引入了多类边的概念，使其无论在结构上还是码率的选择上都更为灵活，因而更容易设计出所需要的LDPC码。

LDPC码的度分布体现了各类节点连接的、由变量节点度分布多项式和校验节点度分布多项式表示的数量以及码率等重要信息。度分布在设计校验矩阵的过程中至关重要，一种好的度分布更容易设计出性能优异的LDPC码。当给出一种度分布时，就给定了一个LDPC码的集合。密度进化(density evolution, DE)[6]是一种用于分析在置信传播(belief propagation, BP)译码条件下给定LDPC码集合收敛行为(即译码门限值)的方法，其中译码门限值被定义为当编码块长度达到无穷大时译码错误概率收敛到零的最大信道噪声。密度进化的一个明显缺点就是计算量非常大，因此其近似方法(称为高斯近似[7])常被用于度分布的优化。

为了满足连续变量量子密钥分发应用场景对LDPC码的要求，本文提出了一种针对具有3种边类型且部分变量节点度为1的MET-LDPC码的设计方法，这种结构的码字可以分块设计且只需设计校验矩阵的左边部分。在设计过程中首先进行度分布优化[8]，得到满足该MET-LDPC码结构要求的度分布，然后再根据度分布使用基于多路径外在信息度策略[9]的渐进边增长(progressive edge growth, PEG)算法[10]去设计该码字校验矩阵的左下角以及通过掩模的方式去设计左上角，最后再与校验矩阵右边部分合并成整个MET-LDPC码的校验矩阵。仿真结果表明，这种设计方法是可行性的。

1 MET-LDPC码概述

MET-LDPC码有多种类型的边，其度分布多项式表示出了各种类型节点连接的每一类边数量以及这种类型节点所占比例。变量节点度分布多项式和校验节点度分布多项式分别表示为

(1)

(2)

(1)—(2)式中：b,d,r,x都是矢量；nv表示变量节点的种类数；nc表示校验节点的种类数。令ne表示MET-LDPC码边的类型数，nr表示可能用于传输码元比特的信道种类数。每种类型的节点定义表示为

(3)

(3)式中：x=[x1,x2,…,xne]；d=[d1,d2,…,dne]。每种类型的变量节点定义为

(4)

(4)式中，bi表示该种类型的变量节点对应的码字是否在第i类信道上传输。例如，对于二进制输入的加性高斯白噪声(binary input additive white Gaussian noise，BI-AWGN)信道，变量节点对应的码元比特在信道进行传输，即不是删余变量节点，则b=[0,1]，否则b=[1,0]。

度分布多项式中vi和ui都是不大于1的正实数，对应于该类型节点的比例。无删余变量节点的MET-LDPC码码率Rate的计算式为

(5)

2 MET-LDPC码结构

连续变量量子密钥分发(continuous-variable quantum key distribution, CV-QKD)应用场景需要码率低、码长长、性能好的MET-LDPC码，因此，在设计MET-LDPC码时要引入大量低度数分布的变量节点，以保证设计的低码率LDPC码性能接近香农限；使用边连接度数较大的变量节点，以保证最小汉明距离随着码长的增加而增加，从而构造出性能好的低码率LDPC码。图1所示的MET-LDPC码Tanner图便符合上述要求。

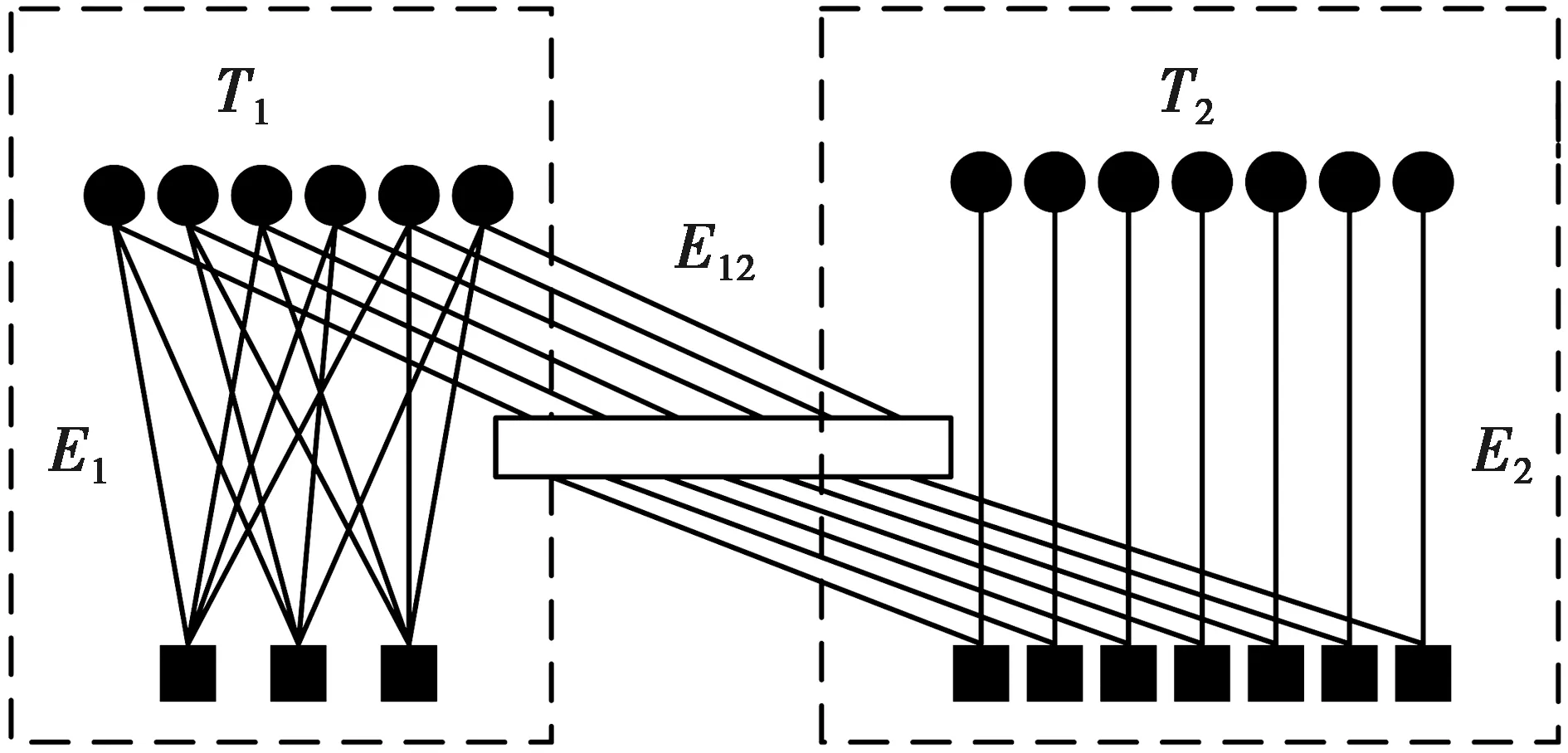
图1 MET-LDPC码Tanner图

图1中，Tanner图可以拆分成2个子Tanner图T1和T2，E12表示连接T1和T2的边。E12所连接的变量节点都在T1中，校验节点都在T2中。所有度数为1的变量节点都在T2中，且T2的变量节点的度数都为1，每个校验节点仅仅与一个度数为1的变量节点相连接。在T1中除了连接的边E12，其余结构与一般非规则LDPC码相同。从直观上看，T1与T2通过边E12串联构成。

与图1所示Tanner图对应的MET-LDPC码的校验矩阵结构如图2所示。

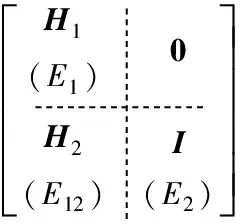
图2 MET-LDPC码校验矩阵结构

图1中，T1的校验节点与T2的变量节点之间没有连线，对应于图2右上角的全零矩阵。T2中变量节点的度都为1且通过边E2与T2中的校验节点一一对应相连，边E2可用图2右下角的单位阵表示。T1中的变量节点通过边E12与T2中的校验节点相连，对应图2左下角的矩阵H2。连接T1中变量节点与校验节点的边E1则对应图2左上角的矩阵H1。图2中MET-LDPC码校验矩阵右上角的全零矩阵和右下角的单位阵已经确定，所以整个MET-LDPC码设计就是图2中矩阵H1与H2的设计。

3 MET-LDPC码度分布优化

MET-LDPC码的度分布优化[11]是一个通过密度进化、高斯近似、差分进化[12]等算法找到满足译码门限值要求的MET-LDPC码度分布多项式的过程。本文设计的MET-LDPC码针对BI-AWGN信道，用到的密度进化、高斯近似也是相应地针对BI-AWGN信道的。本文设计的MET-LDPC码不考虑删余变量节点。

优化得到的MET-LDPC码度分布始终要满足码率以及变量节点和校验节点连接的各类边数量相等这两个约束条件。令矩阵Ev表示各类变量节点连接的各类边数量，矩阵Ec表示各类校验节点连接的各类边数量，矢量vT表示变量节点多项式各项系数vi，矢量uT表示校验节点多项式各项系数ui，可得

(6)

(7)

vT=[v1,v2,…,vnv]T

(8)

uT=[u1,u2,…，unc]T

(9)

(6)式中，di,j是非负整数，表示第i类变量节点连接的第j类边的数量；(7)式中，gi,j是非负整数，表示第i类校验节点连接的第j类边的数量。于是变量节点与校验节点连接的各类相等边以及码率的约束关系便转换为

Evv=Ecu

(10)

(11)

定义矩阵

(12)

(13)

(12)式中，1nv、1nc分别表示长度为nv、nc的全1矢量。那么(10)—(11)式可以表示为

AX=0

(14)

(14)式中，0是长度为nv+nc的全0矢量。如果Ev、Ec、X可以使(14)式成立，便可以构成一个MET-LDPC码的度分布多项式。通过(6)—(13)式，度分布优化转换为在给定参数nv、nc、ne、Rate的条件下，找到使得(14)式成立，同时译码门限值value足够大的Ev、Ec、v、u。Ev和Ec决定了后续校验矩阵设计时各子矩阵的列重和行重，v和u决定了各种列重和行重的比例。整个度分布优化的过程分为内优化和外优化两部分，其中内优化是根据给出的Ev、Ec、Rate找到使译码门限值最大的v和u。算法1为内优化算法。

算法1 内优化算法

输入：Ev，Ec，Rate

输出：X，value

1.根据输入数据生成矩阵A；

2.计算满足(14)式并且元素全是正数的矢量X的个数p；

3.p==0，则输出全零矢量X且value值为0；p==1，则输出对变量节点度分布多项式系数归一化后的唯一矢量X，以及此时高斯近似计算出的、由A与X构成的、MET-LDPC码度分布多项式的门限值value;p>1，则对X执行差分进化算法，找到并输出与A构成的MET-LDPC码度分布多项式高斯近似门限值最大的X以及该最大门限值value。

外优化是找到合适的Ev和Ec，使其与经过内优化处理后得到的v和u构成的MET-LDPC码度分布译码门限值足够大。算法2为外优化算法。

算法2 外优化算法

输入：nv，nc，ne

输出：Ev，Ec，v，u

1.执行差分进化算法的初始化步骤，根据输入随机产生Np个Ev和Ec，其中Np为差分进化算法中的种群数量；

2.对产生的Ev和Ec依次执行内优化，得到对应的X与value，若有value的值超过了设定的门限值，则对该度分布执行密度进化算法，得到更准确的门限值并更新value。若更新后的value仍大于设定的门限值，则结束外优化，输出Ev、Ec、v、u。否则继续执行步骤2，直到所有Ev和Ec均已进行内优化，执行步骤3；

3.执行差分进化算法的交叉、变异、选择3个步骤，产生新的Ev和Ec，执行步骤2。若步骤3执行次数达到设定的值，则结束外优化，度分布优化失败。

4 MET-LDPC码设计及译码

本文设计的MET-LDPC码对应的校验矩阵可以分为4个子矩阵，并且右上角的子矩阵是一个全零矩阵，右下角的子矩阵是一个单位阵，只需要根据优化后的度分布对左上角和左下角的矩阵进行设计，再将4个子矩阵合并便完成了整个MET-LDPC码的设计。在MET-LDPC码设计过程中，多路径外在信息度(extrinsic message degree，EMD)[13]常常被用来作为判断设计性能的依据，EMD定义为只与变量节点集合(或者一个环)中的一个变量节点相连的校验节点的数量。EMD值越大，这一变量节点集合(或者环)在信息传递过程中获得的外信息就越多，性能也就越好。

4.1 左上角矩阵设计

左上角矩阵对应于MET-LDPC码Tanner图的边E1，与传统LDPC码的结构相同。本文通过在基于平方剩余(quadratic residue, QR)码构造的具有准循环结构的低密度奇偶校验(quasi cyclic LDPC，QC-LDPC)码[14]的基矩阵上进行掩模的方式，完成左上角矩阵的设计。掩模思路是优先掩模掉QC-LDPC码基矩阵中环穿数最多的循环置换矩阵(circulant permutation matrix, CPM)对应的基矩阵中的元素，当环穿数最多的CPM不止一个时，则通过EMD来决定掩模的位置。掩模依据在于CPM性能的好坏与其环穿数多少有关，环穿数越多，性能越差，应先被掩模掉。当存在环穿数最多的CPM不止一个时，则统计其成环的EMD值，EMD值越小，性能越差，应先进行掩模。掩模算法具体过程见算法3。

算法3 掩模算法

输入:Rate,length//需要构造的码的码率和码长

输出：Hm×n//m行n列矩阵

1.根据输入的两个参数从已有的基于QR码构造的QC-LDPC码的基矩阵中按环数最少的原则截取大小为m行n列的矩阵Hm×n

2.l=3//基于QR码构造的QC-LDPC码没有4环

3.定义矩阵B并初始化为全1的矩阵//记录掩模的位置并用于判断掩模后的度分布

4. Loop

5.EMD0=∞

6. 用环穿数统计算法得到对应的L以及Nm×n

7. ifNm×n是全零矩阵then

8.l=l+1

9. go to Loop

10. end if

11. ifNm×n有唯一的最大值then

12. 将矩阵B中与最大值对应位置元素置0并根据B更新Hm×n

13. else

14.EMD0取L里面的最大值

15. whileEMD0不等于L中的最小值do

16. 记录Nm×n中最大值的位置

17.EMD0取L仅小于它的最大值

18. 用环穿数算法重新得到L，Nm×n

19. ifEMD0是L中的最小值且Nm×n中没有唯一的最大值then

20.l=l+1

21. go to Loop

22. end if

23. ifNm×n里面的元素有唯一个最大值then

24. 矩阵B中与最大值对应位置元素置0并根据B更新Hm×n

25. end if

26. end while

27. end if

28. ifHm×n满足度分布要求then

29. go toend Loop

30. end if

31.end Loop

掩模算法从基于QR码构造的QC-LDPC码基矩阵中截取矩阵Hm×n进行循环掩模，如果Hm×n的度分布与经过度分布优化得到的结果一致，则结束掩模。在掩模过程中，每次确定掩模的位置之前都要统计每个CPM的环穿数。

4.2 左下角矩阵设计

算法4 多路径EMD策略

输入：vj//当前正在处理的变量节点

输出：ci//挑选的校验节点

1.fork=1 todvjdo//dvj表示变量节点vj的度

2. ifk==1 then

3. 从当前度最小的校验节点中随机挑选一个输出

4. else

8. else

10. 用B表示A中度最小的节点的集合；

11. 找出从vj到B中各个校验节点的路径数；

12. 用C表示B中路径数最少的节点的集合；

13.C中元素唯一则输出该唯一元素，否则计算C中每个元素到vj的路径的EMD值，并求其平均值，然后选平均值最大的校验节点输出

14. end if

15. end if

16.end for

多路径EMD策略减少了设计过程中挑选校验节点时的随机性，从而能构造出性能更好的码。其具体设计过程为执行文献[9]中的构造QC-LDPC码的PEG算法，当需要挑选与正在处理的变量节点相连的校验节点时，执行多路径EMD策略挑选出与之相连的校验节点。图3是一个从变量节点vj出发扩展到深度等于2的例子，其中黑色圆圈表示变量节点，黑色方框表示校验节点。

图3 变量节点vj扩展至深度等于2

4.3 MET-LDPC码译码

本文采用LOG-BP校正子译码算法进行MET-LDPC码的译码，令yi表示从BI-AWGN信道接收到的对应于第i个变量节点的信号幅度值，δ表示信道噪声的均方差，H表示MET-LDPC码校验矩阵，Ll(rji)表示第l次迭代时校验节点j传递给变量节点i的对数似然值，Ll(qij)表示第l次迭代时变量节点i传递给校验节点j的对数似然值，Ll(qi)表示变量节点i第l次迭代时的总信息似然值，Rji表示从与校验节点j相连的变量节点集合中扣除变量节点i，Cij表示从与变量节点i相连的校验节点集合中扣除校验节点j。MET-LDPC码译码算法具体步骤见算法5。

算法5 MET-LDPC码译码算法

1.初始化，对于每个变量节点i，计算其初始对数似然值L0(qij)，并利用原始随机矢量U计算其校正子CB

(15)

CB=HUT

(16)

2.校验节点信息更新，计算Ll(rji)

(17)

(18)

(19)

(17)式中，sgn是符号函数；(18)式中，Φ(x)为

Φ(x)=Φ-1(x)=-ln(tanh(x/2))

(20)

根据CB的值判断奇偶校验类型，是奇校验则Ll(rji)取相反数，是偶校验则Ll(rji)的值不变

3.变量节点信息更新，计算Ll(qij)

(21)

(22)

4.译码判决

(23)

如果判决码字w满足CB=HwT或者达到设定的最大迭代次数，则结束译码；否则，回到第2步继续迭代。

5 仿真结果

基于前述设计方法，本文设计了两个基矩阵大小都为42行52列、CPM大小分别为1 000和800的MET-LDPC码。其码长分别为52 000和41 600，码率均为0.192 3。

根据第2节MET-LDPC码结构可知，设计的MET-LDPC码有3类边。在做度分布优化时设定变量节点类型数nv=3，校验节点类型数nc=4，相应的度分布函数为

(24)

(25)

由(24)—(25)式可知，需设计的MET-LDPC码基矩阵左侧大小为42行14列并且有4列列重为7，10列列重为12。其中左上角矩阵大小为4行14列并且有4列的列重为3，10列的列重为2；左下角矩阵大小为38行14列，其中有4列的列重为4，10列列重为10。

从(98，47)QR码构造的QC-LDPC码基矩阵中按环最少的原则截取一个4行14列的子矩阵用于掩模完成左上角矩阵设计。在整个左侧矩阵的度分布条件下，结合已经设计完成的左上角矩阵，执行基于多路径EMD策略的PEG算法，完成左下角矩阵设计，最终将各个部分合并以获得最终的MET-LDPC码。在相同的参数条件下，还构造了两个左上角和左下角都采用PEG算法设计的MET-LDPC码。所有码字都采用改进的LOG-BP校正子译码算法进行性能仿真，最大迭代次数为100。CPM大小为1 000的两个MET-LDPC码性能仿真曲线如图4所示，CPM大小为800的两个MET-LDPC码性能仿真曲线如图5所示。

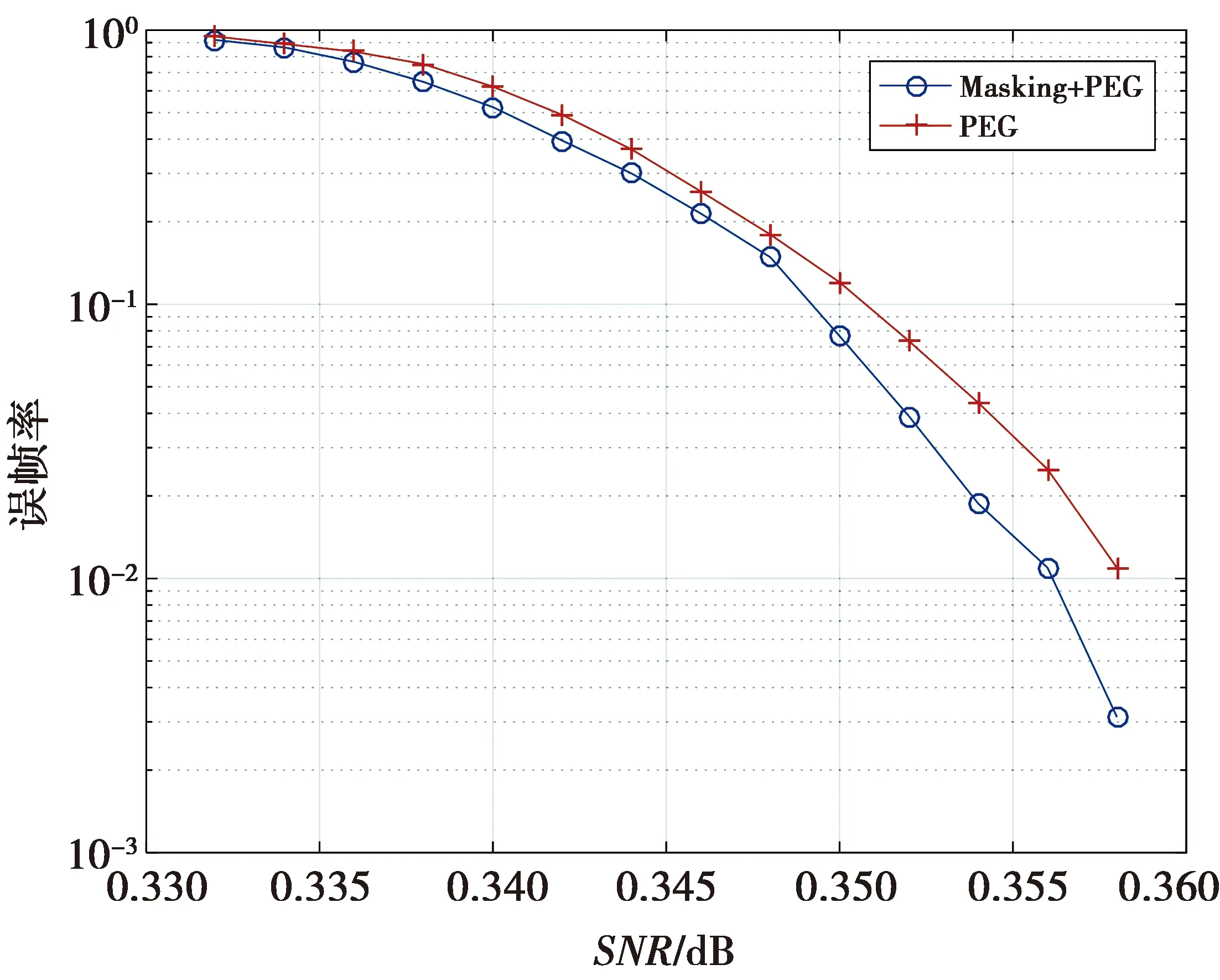
图4 CPM大小为1 000的MET-LDPC码性能对比

图5 CPM大小为800的MET-LDPC码性能对比

由仿真结果可知，在相同参数条件下，本文设计的MET-LDPC码性能优于仅用PEG算法设计的码。

6 结 论

本文针对一类具有3种边类型且部分变量节点度为1的MET-LDPC码，提出了一种掩模加基于多路径EMD策略的PEG算法的设计方法。掩模不仅去掉了对译码性能影响较大的CPM,还减少了影响译码性能的短环，保证了左上角矩阵的性能，为Tanner图右侧部分在译码时提供更准确的信息。在整个左侧矩阵的度分布条件下，基于已经设计完成的左上角矩阵，用带有多路径EMD策略的PEG算法设计左下角矩阵，可以更有针对性地挑选校验节点，从而保证整个MET-LDPC码性能。在保证优化后度分布的条件下，本文设计出了两个码长分别为52 000和41 600、码率均为0.192 3的MET-LDPC码。仿真表明，在相同参数条件下，本文比PEG算法性能更优。