Costas序列短波MFSK通信时频联合同步方法

李景慧，李国军，叶昌荣，王尊立

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 超视距可信信息传输研究所，重庆 400065；3.重庆邮电大学 光电工程学院，重庆 400065)

0 引 言

在现代数字通信系统中，同步性能是评估系统性能的关键指标，是可靠数字通信的重要保证。传统同步方法一般通过检测位于数据帧头部的同步码实现，其性能与同步码的长度相关。同步码太短，在低信噪比条件下将无法被识别；而同步码太长，又将占用过多的信道资源，影响通信效率。因此，为恶劣环境下的短波通信系统设计更好的同步码和更稳定的检测算法已经成为研究同步的核心问题。实现同步的主要方法有相关法[1]、最大似然法(maximum likelihood, ML)[2-3]和似然比检验(likelihood ratio test, LRT)[4]等3种方法。其中，相关法具有最低的复杂度，且最容易实现[5]，但是在低信噪比条件下的性能最差；最大似然法和似然比检验效果好于相关法，但计算比相关法复杂[6]。提高相关法在恶劣环境下的性能，降低算法实现难度，对于提高恶劣环境下的通信质量具有重要意义。

同步码中使用较多的是伪随机码(PN码)[7-8]，延迟相关法和本地相关法是两种常用的同步算法。延迟相关法具有较大的频率偏移容限，但是在低信噪比和多径信道下，其自相关函数曲线在峰值处变化平缓，无法精确指示同步起始点。本地相关法具有尖锐的自相关峰值，准确度高于延迟相关法，能精确地指示同步起始点，抗噪声和多径能力强，但是对频偏敏感。

本文提出了一种基于Costas序列的时频联合同步方法，使用Costas序列作为同步码，将传统的滑动窗口法扩展到时频域中，可以同时估计时延和频偏，具有更好的抗噪声和抗频偏性能。

1 Costas序列特性分析

1.1 Costas序列定义及构造方法

任意每行每列有且仅有1个元素等于1、其余元素都为0的n×n阶矩阵称为置换矩阵。Costas序列是一类特殊的置换矩阵，它与自身任意方向的平移副本之间都至多有1个元素“1”重合，如矩阵A所示(其序列表示为[4,1,6,7,5,8,3,2])。

(1)

(2)

由于置换矩阵A是有限维的，元素ai,j构成的序列是有限长的，因此在非循环差异函数C(r,s)中，当i+r或j+s超出区间[1,N]时，取ai+r,j+s为0。非循环差异函数满足(3)式的n×n阶置换矩阵称为n阶Costas序列[9]。

(3)

Costas序列构造方法[9-11]分为计算机穷举搜索法和基于有限域理论的构造法两种方法。计算机穷举搜索法会穷举出所有的置换矩阵，并检测矩阵是否满足Costas序列的定义，满足则输出该Costas序列。计算机穷举搜索法可以输出满足所需阶数的所有Costas序列，但由于穷举法的复杂度较高，计算机穷举法所能搜索的阶数是有限制的[9]，在构造阶数较大的Costas序列时需要使用基于有限域理论的构造方法。基于有限域理论的构造法有Welch构造法、Golomb构造法和Lempel构造法[9-10]等多种方法。

本文使用8阶Costas序列，计算机穷举搜索法可以满足使用。如无特别说明，本文中出现的Costas序列均由计算机穷举搜索法生成。

1.2 Costas序列相关特性分析

对于一个Costas序列([4,1,6,7,5,8,3,2])，称[4,1,6,7,5,8,3,2]为其序列表示，(1)式为其矩阵表示。Costas序列的自相关性体现在其矩阵表示上。为了分析矩阵的相关特性，定义函数RAB(a,b)为n×n阶矩阵A和B的相关函数。计算相关函数的方法如图1所示，矩阵A不动，矩阵B沿x轴和y轴进行移动，其中a为矩阵B沿x轴移动的单位数(-n+1≤a≤n-1)，b为矩阵B沿y轴移动的单位数(-n+1≤b≤n-1)，则函数RAB(a,b)的值为矩阵B移动后，两矩阵中“1”单元格重合的个数。当矩阵A和矩阵B相等时，称RAB(a,b)为自相关函数[12]。

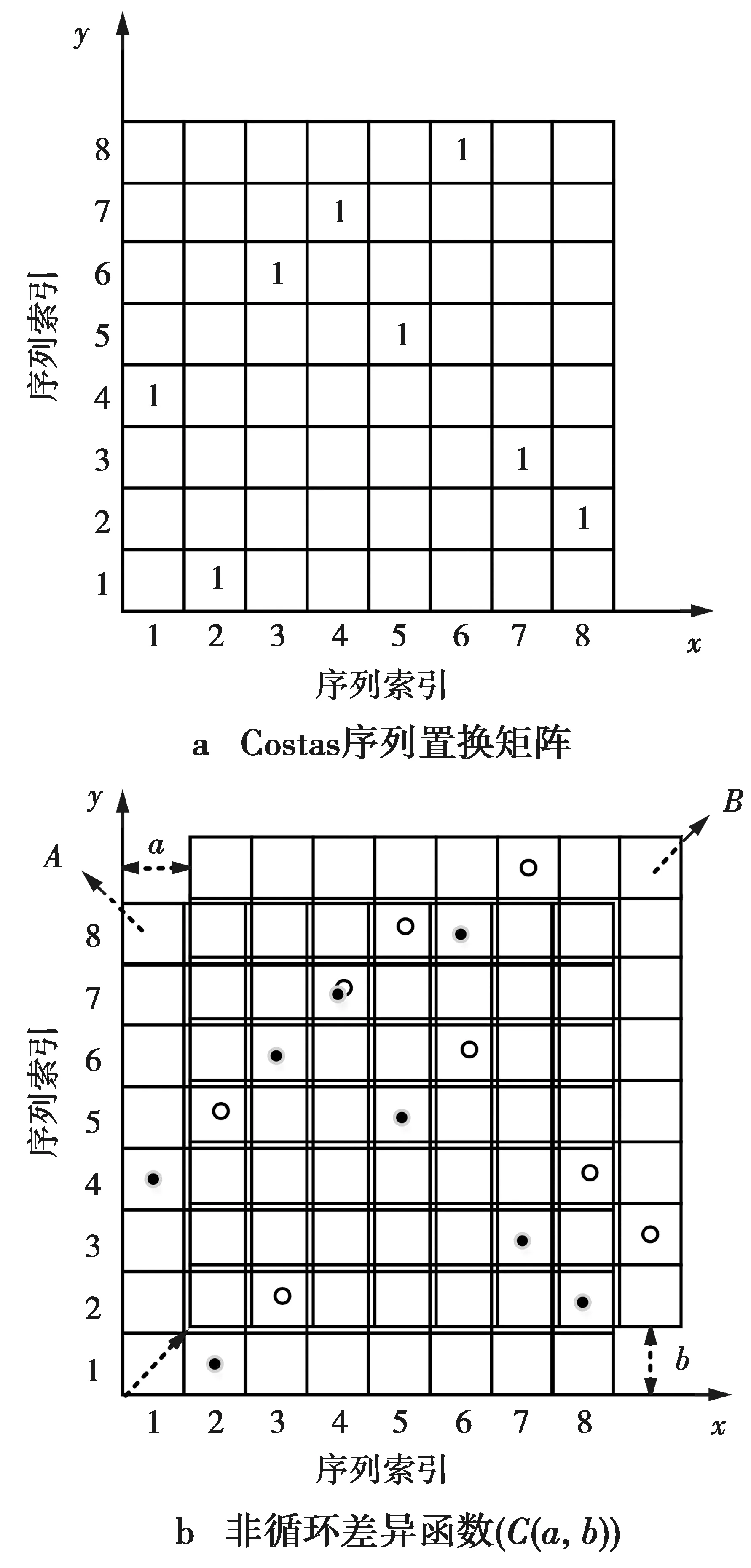
图1 矩阵相关计算示意图

图2是一个8阶Costas序列的自相关函数计算结果，峰值幅度为其阶数n，非峰值处的最大幅值为1。不同Costas序列做同步码会表现出不同的性能。图3和图4分别为Costas序列1和序列2自相关函数示意图。图3中，序列1存在“相邻1”，导致自相关函数存在临峰(序列中相邻两个元素的差值为1的情况称为“相邻1”，序列自相关函数中与峰值相邻的不为0的值称为临峰)，在同步过程中，临峰会对同步造成干扰。而图4 中Costas序列2由于没有“相邻1”的存在，自相关函数中不存在临峰，因此其在同步时受到的干扰会小于Costas序列1。

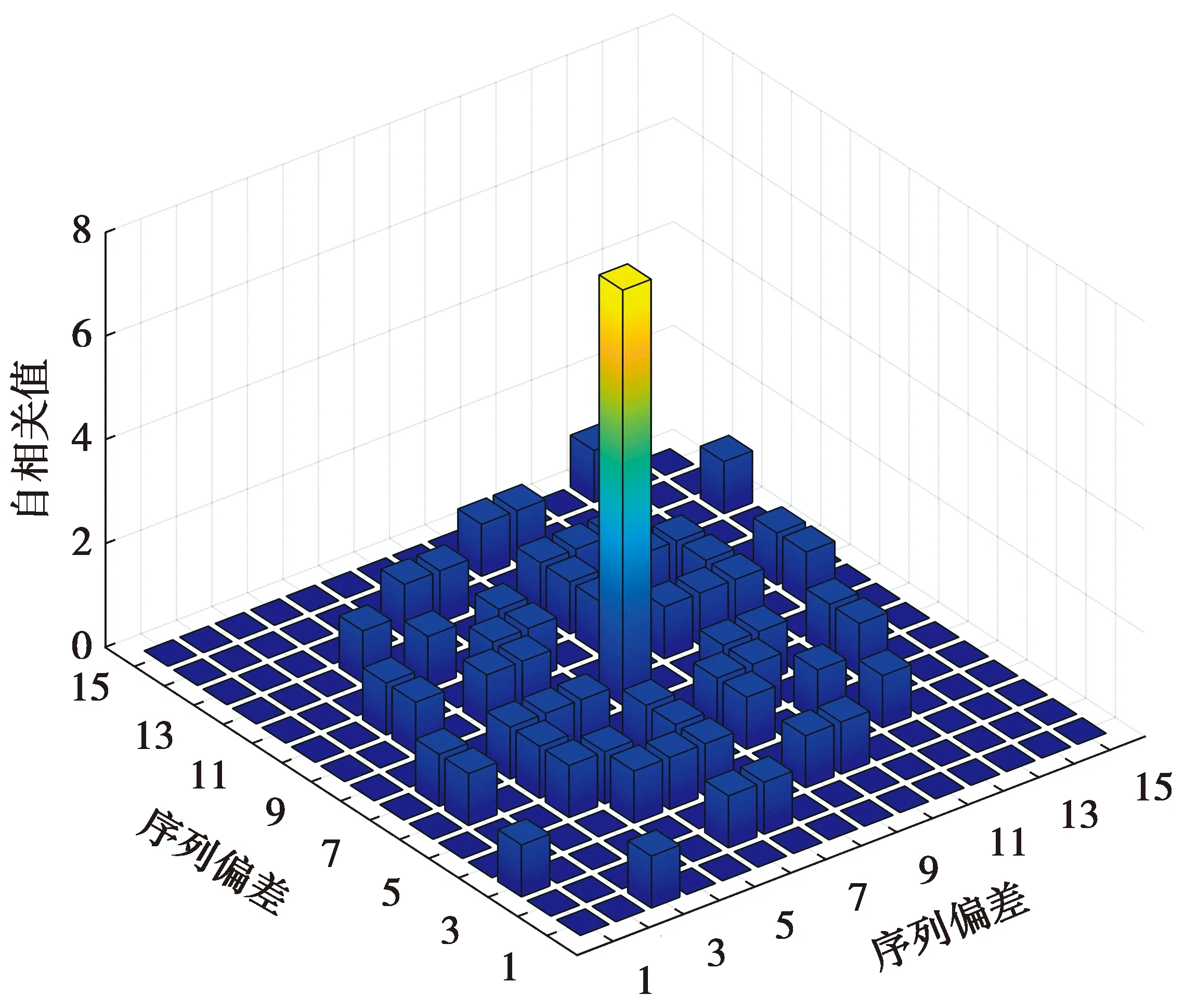
图2 8阶Costas序列自相关函数

图3 Costas序列1自相关函数示意图

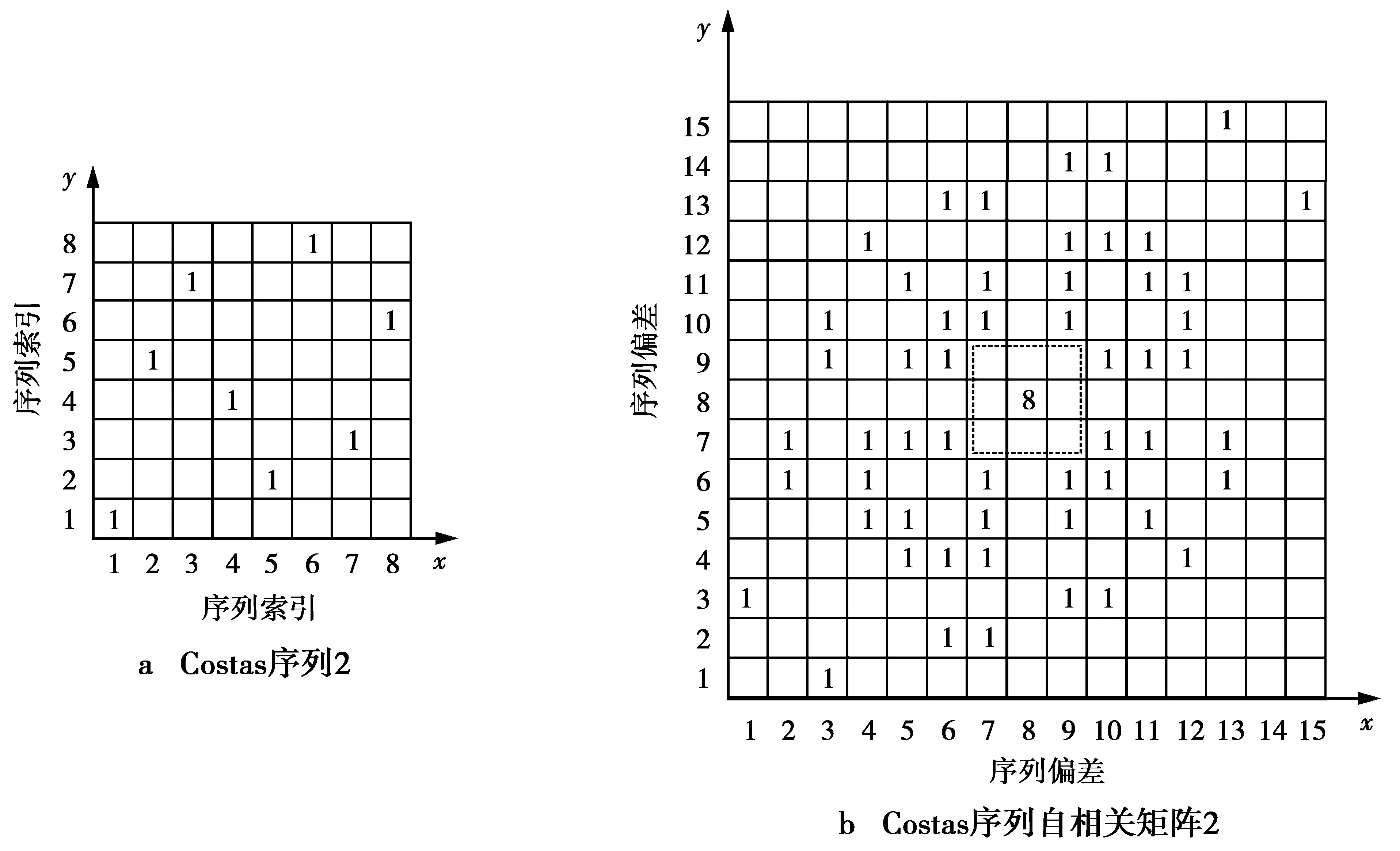
图4 Costas序列2自相关函数示意图

2 基于Costas序列的MFSK信号时频联合同步方法

2.1 粗同步方法

Costas序列经过FSK调制后转换到时频域，信号在时频域的能量分布符合Costas序列自相关特性。本文通过离散短时傅里叶变换(discrete short time Fourier transform, DSTFT)将信号映射到时频域中，如图5所示。

图5 时频谱转换框图

在没有信道干扰的情况下，x(t)的表达式为

(4)

(4)式中：A为幅度；g(t)为窗函数；M为FSK调制阶数；M与Costas序列的阶数n相同；Ts为码元时间；fi为第i个码元符号的调制频率；θi为第i个码元的初始相位。对x(t)采样后得到x(n)，采样率为fs。将时域信号按照码元时间Ts进行分割，分割后的信号集合为{x1(k),x2(k),…,xM(k)}，其中k为一个码元的采样点数，k=Ts·fs。分别对{x1(k),x2(k),…,xM(k)}进行傅里叶变换可得

Xi(W)=F[xi(k)]

(5)

(5)式中，F[·]表示傅里叶变换。将|Xi(W)|进行组合得到信号x(t)的时频谱，表示为

[|X1(W)|,|X2(W)|,…,|XM(W)|]=

TF[x(t)]

(6)

(6)式中，TF[·]表示时频谱变换，其结果为矩阵形式，示意图如图6所示。

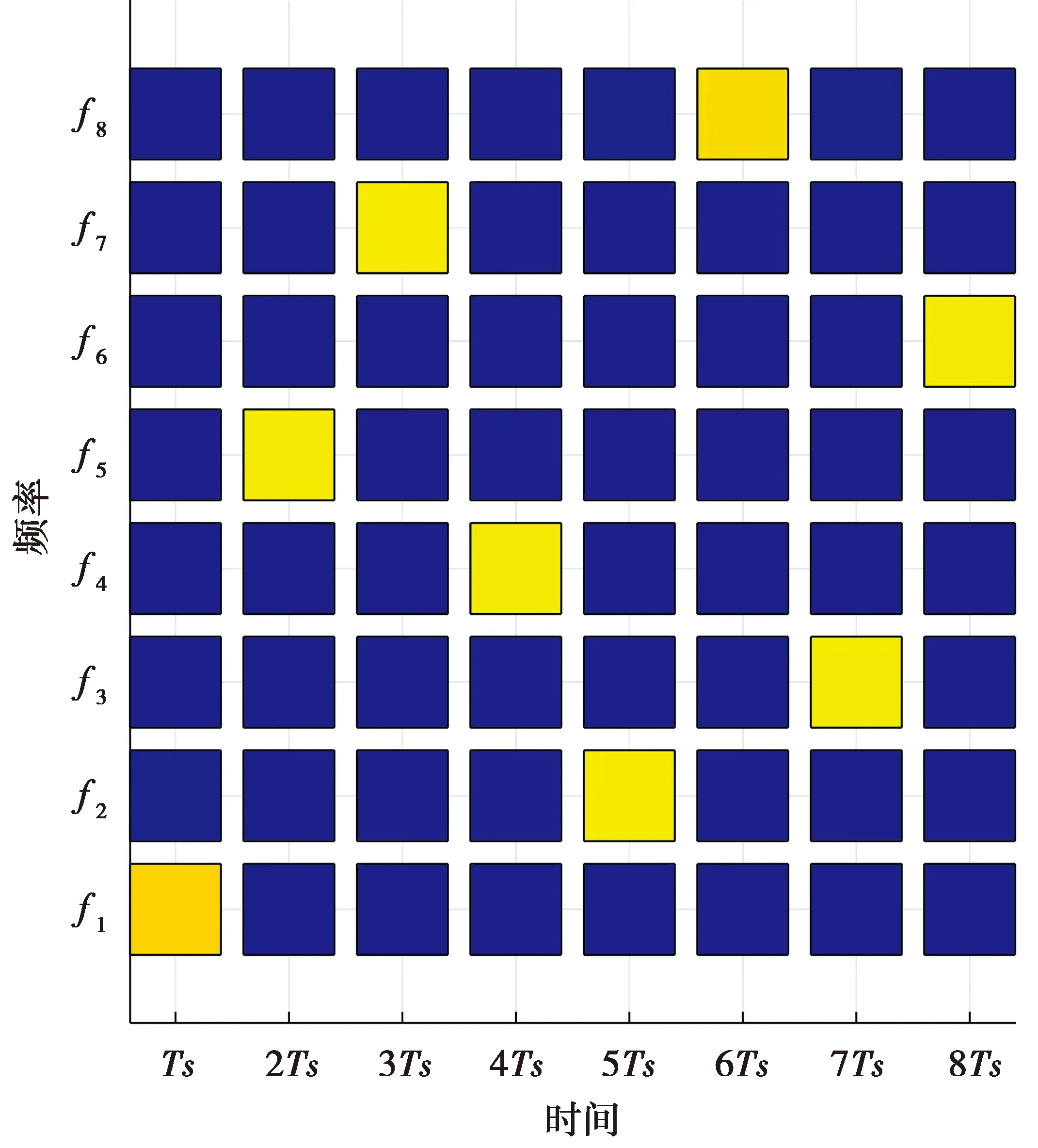
图6 时频谱示意图

假设FTi,j为时频谱在码元时间i、频率j处的能量值，定义在码元时间t、频率f处的判决量为

(7)

(7)式中：n为Costas序列阶数；Ci为Costas序列第i位的值。如果在时频谱范围内判决量大于判决门限，则认为信号存在(在一般情况下取最大相关检测值的60%—90%作为判决门限)。图7所示为iturHFMD信道下的判决量仿真结果，iturHFMD信道参数如表1所示。在信号严重衰落的情况下，通过(7)式定义的判决量依然可以准确指示信号起止位置。

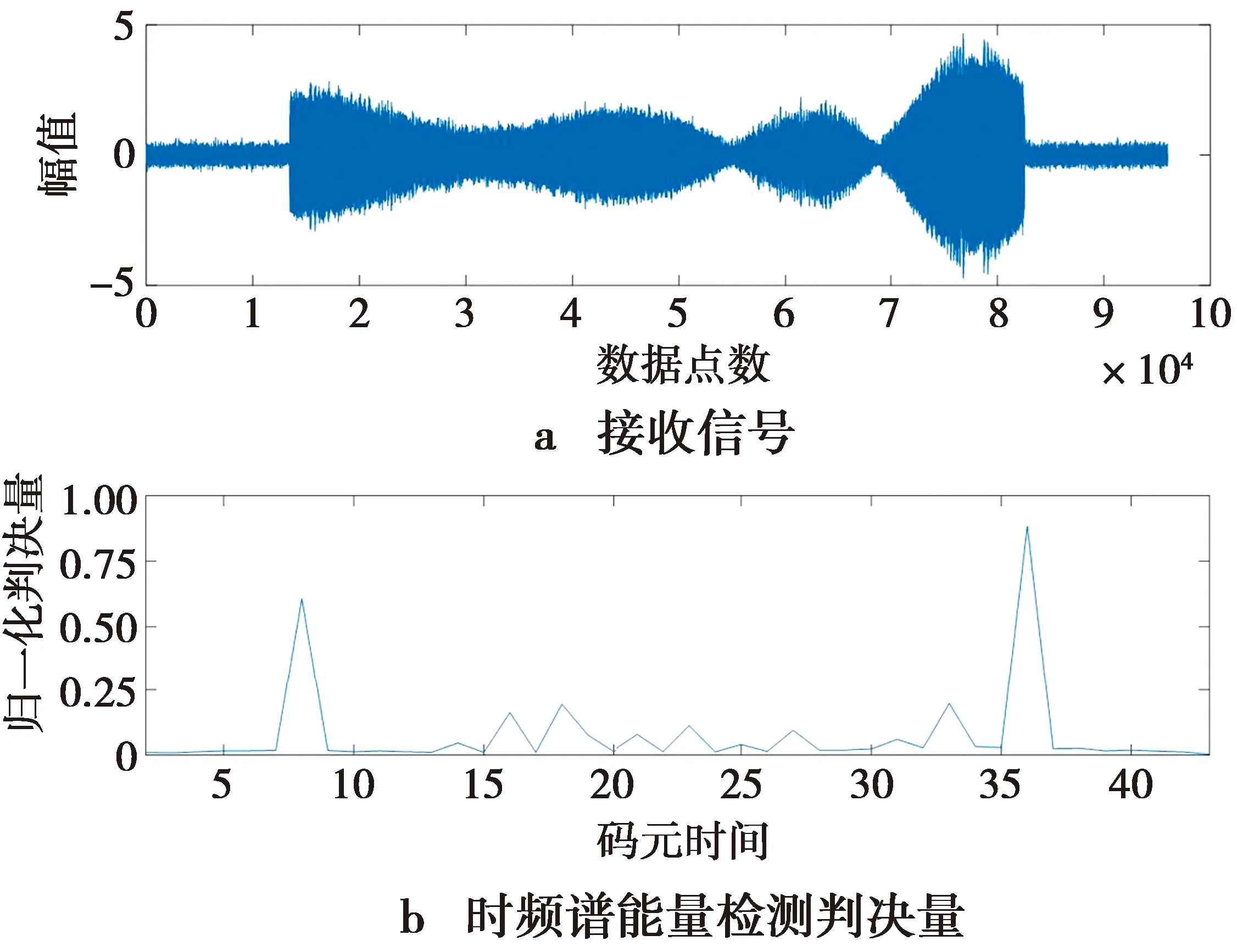
图7 判决量示意图

表1 信道参数

定义第一个大于判决门限的自相关值坐标为[tes,fes]，则tes·Ts为时间粗估计值，fes·fs/N为频率粗估计值，其中N为傅里叶变换点数。

滑动相关后的时间估计精度为Ts，频率估计精度为fs/N=1/NΔT，其中ΔT为采样间隔，NΔT为码元时间。提高时延估计精度，需要减小码元时间Ts，而Ts的减小会使得频率估计精度减小。为了同时提高时间估计精度和频偏估计精度，使短时傅里叶变换中窗函数的步进长度ΔL为Ts/K，其中K为正整数。同时使用过采样(补零)提高频谱分辨率，过采样系数定义为E。K=4时的窗函数步进示意图如图8所示。

图8 DSTFT步进示意图

图9为E=2、K=4的参数条件下，信号x(t)的时频谱。此时的时间估计精度为Ts/K，频率估计精度为1/ENΔT。通过这种方式提高估计精度会导致计算量成倍增加。因此，在适当调整参数K和E后，使用离散频谱分析方法进行精估计。

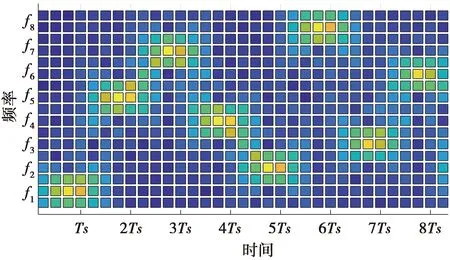
图9 K=4, E=2的时频谱示意图

2.2 精同步方法

由2.1节的tes可以获得一个码元时间的频谱|Xi(W)|，fes为|Xi(W)|的频谱峰值坐标，示意图如图10所示。

图10 基于二倍过采样的非线性频偏估计示意图

图10中，x为经过傅里叶变换的频谱峰值位置，x0为频偏Δf影响后实际的频谱峰值位置。假设窗函数为矩形窗，定义其功率谱函数表达式为[13]

(8)

根据窗函数的重心法则，在n趋近于无穷时有

(9)

根据(8)—(9)式可以计算出x0的位置坐标为[13]

(10)

定义k为峰值谱线坐标，由(10)式可以推导出频偏估计值为

(11)

最终的频率估计为

(12)

在估计时延之前，使用Δf对信号频谱进行纠正。取一个码元时间的信息进行分析，对信号重新进行时频谱变换。由实验数据可得，在时频谱的时域取8个数据点，数据点的值大致服从线性分布，如图11所示。

图11 基于1/4步进滑动窗口的线性时延估计示意图

假设峰值坐标为x，次高值坐标为x-1。定义x到x+3表示的直线函数为Y1(x)，x-4到x-1表示的直线函数为Y2(x)。则Y1(x)与Y2(x)定义如下。

(13)

数据帧实际开始位置x0可以通过计算Y1(x)与Y2(x)的交点所得。

即求解

Y1(x)=Y2(x)

(14)

f(x)=2kx+b1-b2

(15)

所得唯一可行解即为x0，因此，时延精估计值为

Δt=|x-x0|Ts/K

(16)

(16)式中：Ts为码元时间；K为窗函数步进系数。

2.3 窗函数影响分析

DSTFT中窗函数的不同会对同步性能产生影响。令窗函数步进长度ΔL为Ts，假设f1为码元1所代表的频率，f2为码元2所代表的频率。当存在时延时，第一个码元符号的部分信息会延后到x2(k)中。

x2(n)=A1sin[2πf1(n-τ)]+A2sin[2πf2(n-τ)]

(17)

(17)式中：A1表示第一个码元时间的幅度；A2表示第二个码元时间的幅度；τ为时间延迟。此时对x2(k)进行傅里叶变换后，频率f1所造成的频谱泄漏现象会极大地干扰频率f2的主瓣谱线，如图12所示。这种会严重影响频偏估计的干扰，可以通过选择不同的窗函数或者全相位傅里叶变换来减小。

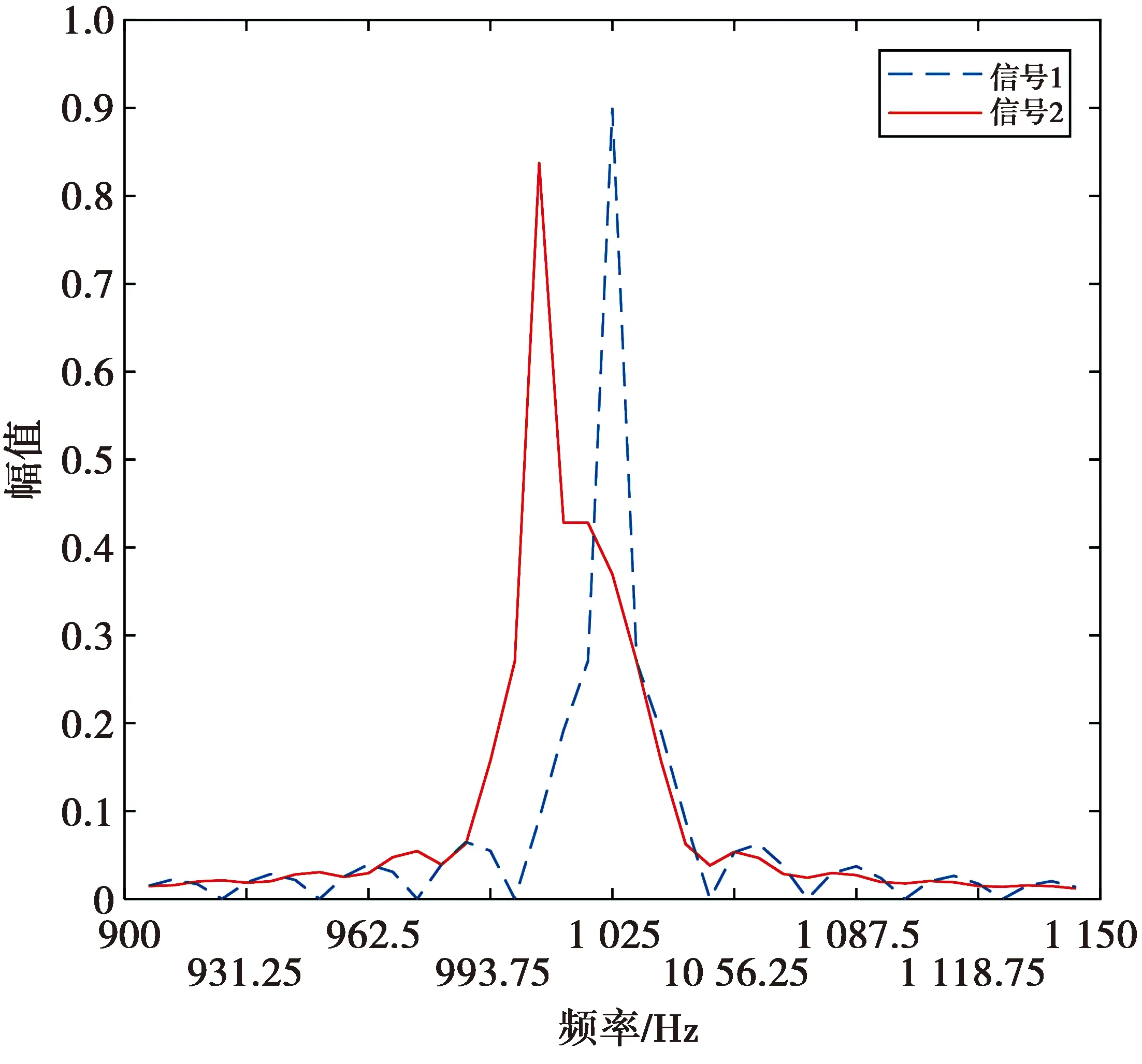
图12 时间延迟分析

3 仿真验证

仿真过程使用8阶Costas序列[1,5,7,4,2,8,3,6]作为同步码，窗函数为矩形窗函数，使用MFSK(M=8)方式对传输序列进行调制，采样率设置为12 kHz，为2倍过采样，窗函数步进长度为1/4码元时间。根据国际电信联盟给出的Watterson模型建议参数[14]，选择中纬度地区的3种短波信道仿真。3种信道参数如表1所示。

图13—图15给出了本文方法在不同判决门限下虚警率和检测率的ROC曲线。在AWGN信道条件下，随着判决门限的逐渐增大，虚警率不断降低，但检测率变化很小。在短波信道中，不添加噪声时的检测性能与添加-20 dB噪声干扰的检测性能相近。综上所述，本文同步方法对阈值不敏感，且具有优秀的抗噪声性能，虽在短波信道中的性能有所下降，但依然可以保证其在短波信道的可用性。

图13 ROC曲线(AWGN信道)

图14 ROC曲线(iturHF信道)

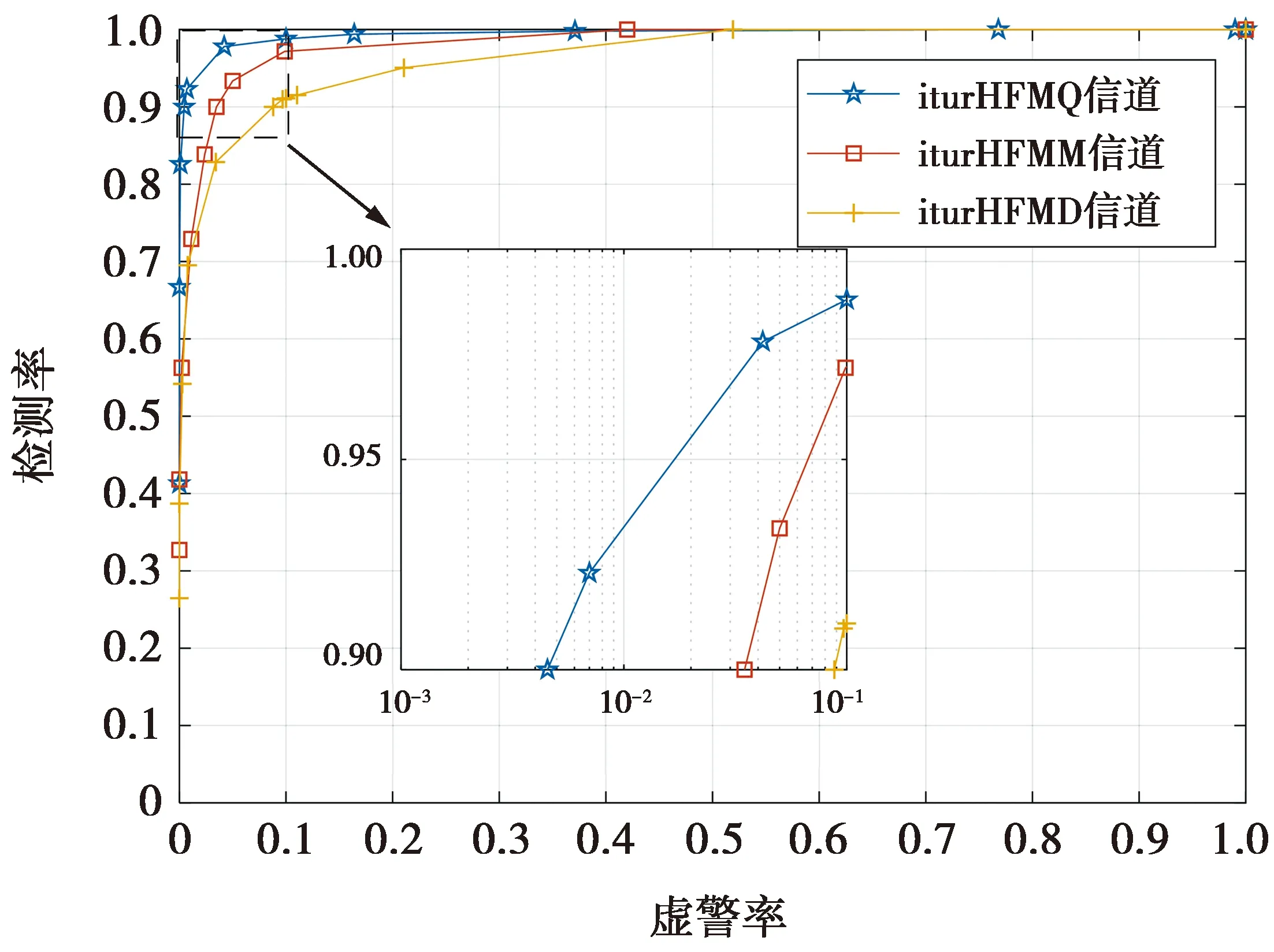
图15 ROC曲线(iturHF信道, -20 dB)

以最大相关检测值的70%作为判决门限，本文同步方法与传统PN码同步方法在iturHFMQ信道下的检测性能如图16所示。传统的PN码同步方法，在信噪比逐渐降低时性能出现陡降；本文同步方法在信噪比为-20 dB时，依然具有可观的检测率，可以有效提高恶劣环境下短波通信的质量。

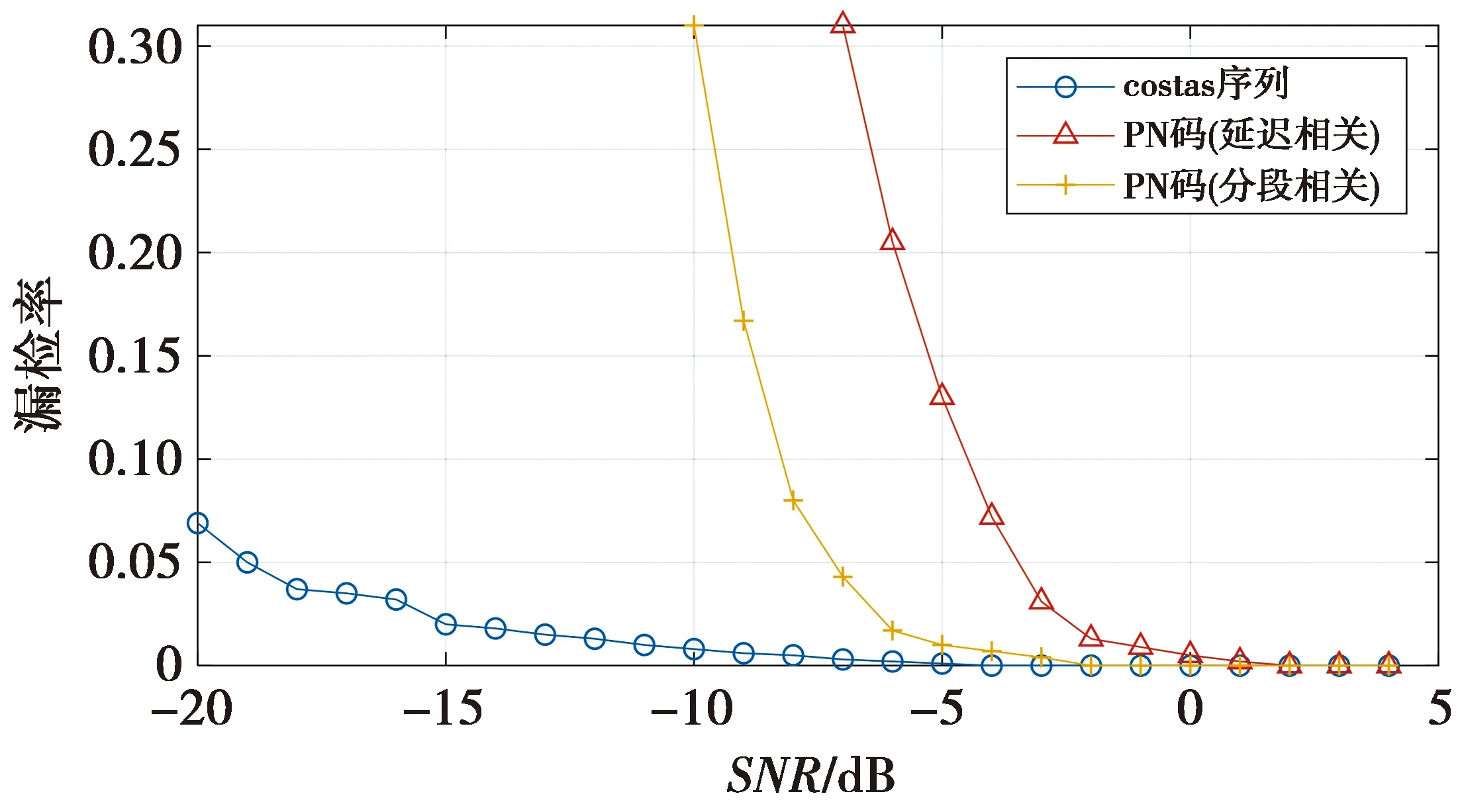
图16 基于Costas序列同步方法的漏检率

图17—图18为本文同步方法在频偏影响下的自相关峰值变化图，仿真信道为iturHFMQ。由于自相关函数是关于时间和频率的参数，需要从两个角度来分析其峰值变化，图17为频域角度的自相关峰值变化图，图18为时域角度的自相关峰值变化图。本文同步方法的自相关峰值幅度主要受频谱泄漏的影响，当频偏越接近1/2频谱分辨率的奇数倍时，影响越大。从时域分析，自相关峰值附近的值相对较低，出现了一个凹陷，验证了本文1.2节中所描述的“相邻1”的影响。在小频偏影响下，相关结果峰值几乎不受频偏的影响，在频偏值造成的影响较大时(接近1/2频谱分辨率的奇数倍)，其相关结果峰值依然可以近似达到无频偏时的70%左右。对比文献[15]中的方法，本文同步方法可以有效减小大频偏对同步造成的影响。

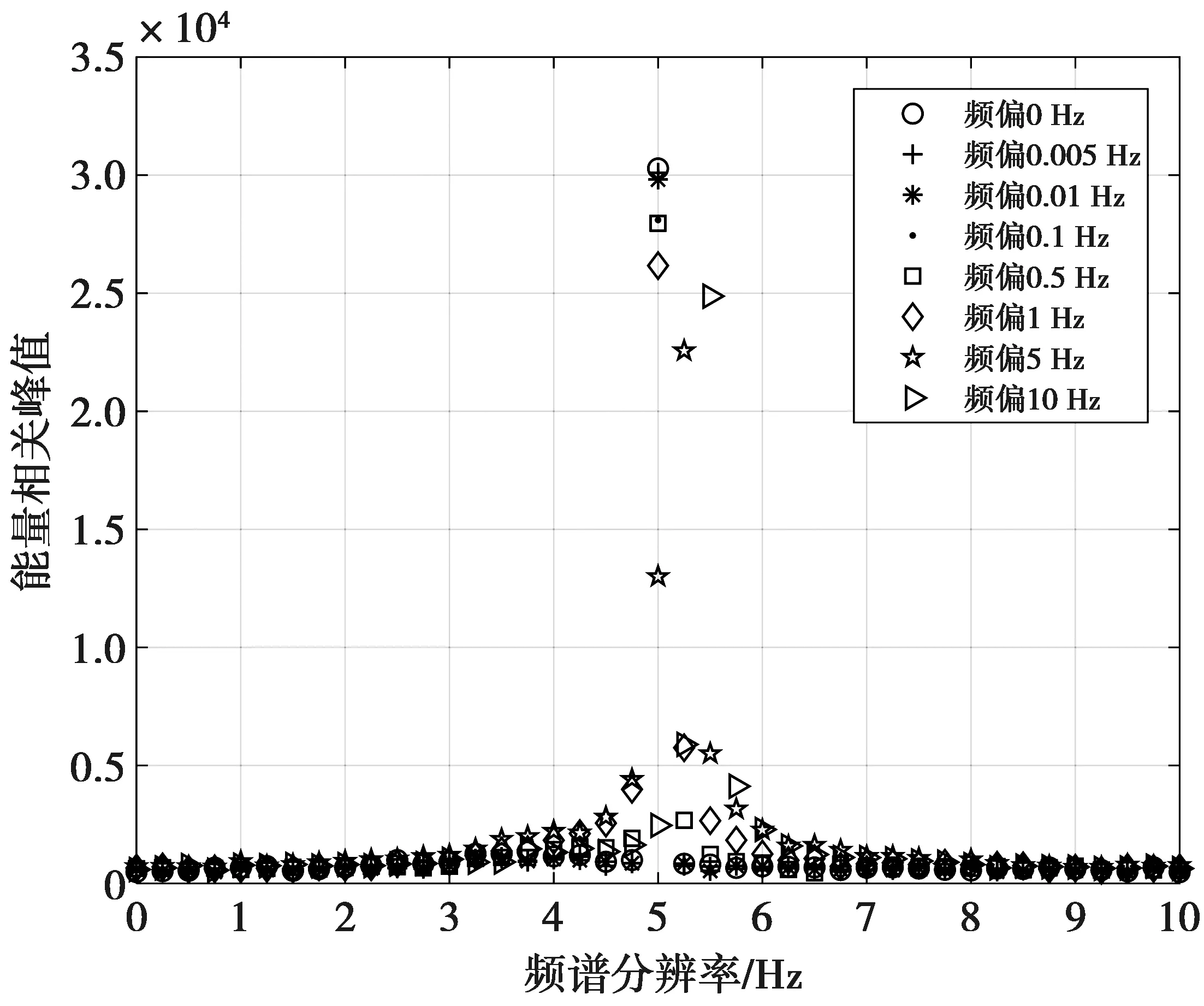
图17 同步相关峰示意图(频域)

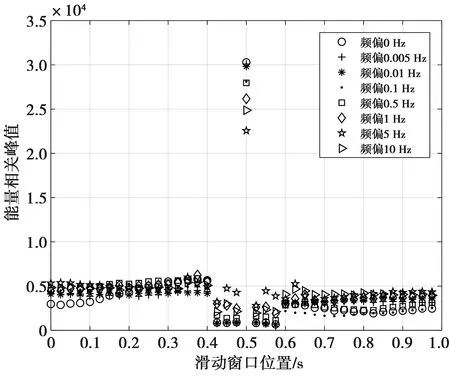
图18 同步相关峰示意图(时域)

图19为本文同步方法与PN码相关法的定时精度对比。图19中，PN码长度与本文使用的同步码长度相同(1.28 s)。由图19可以看出，本文所提出的同步方法在信噪比较低时具有明显的优势。

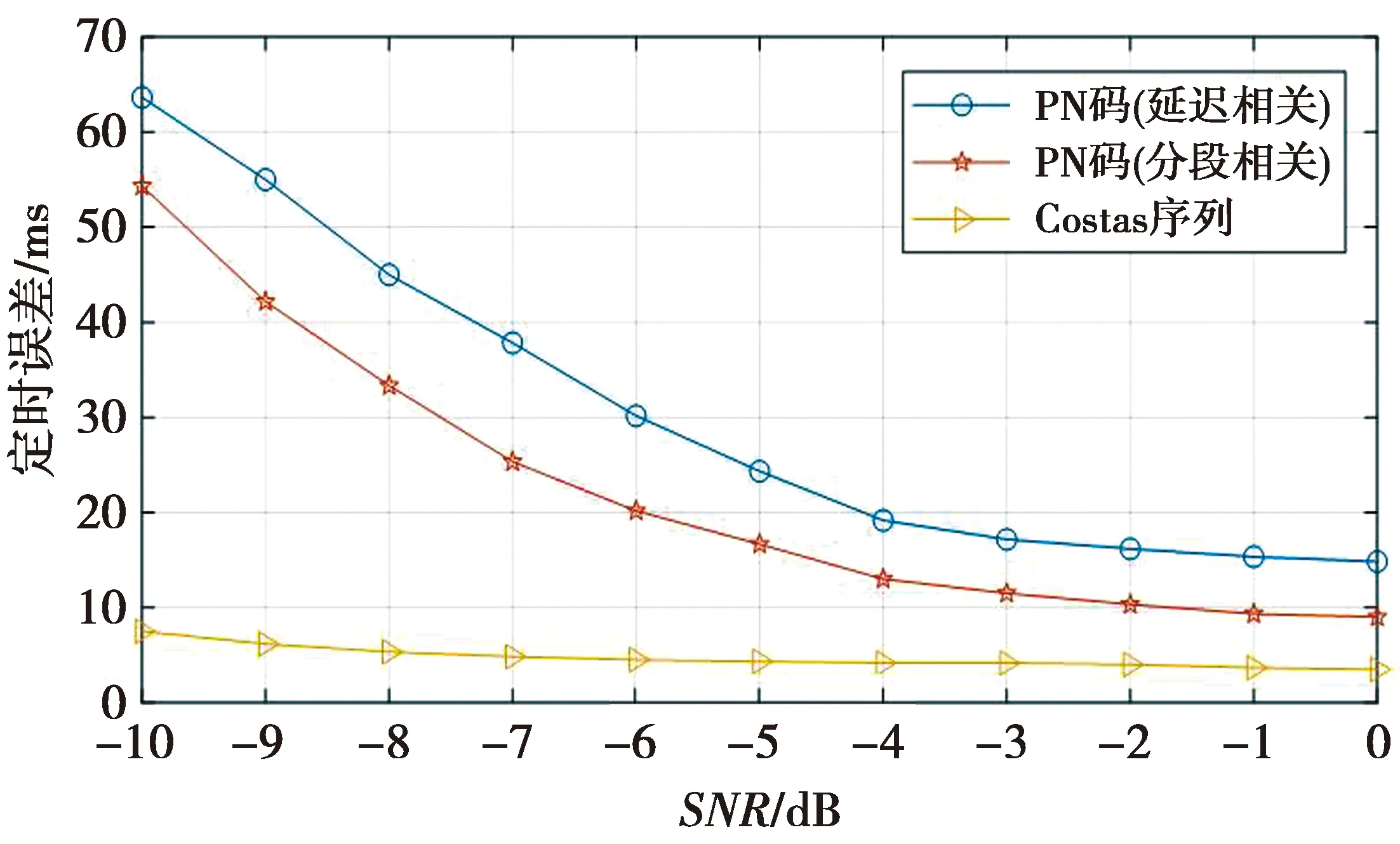
图19 定时误差分析

由于使用了离散频谱分析方法进行精估计，本文同步方法的精度在低信噪比情况下呈现出明显的周期性。设置信噪比为-17 dB，图20和图21为本文同步方法在iturHFMQ信道中的时间估计误差和频率估计误差仿真图。在低信噪比短波信道条件下，本文同步方法依然具有很高的估计精度，但估计误差出现周期性变化的现象。这是由于在精同步过程中，依赖频谱或自相关函数中最高值坐标和次高值坐标的判定，当时间延迟或者频率偏移接近其归一化值-0.5、0、+0.5时会出现最高值坐标或次高值坐标判定错误的情况。以归一化频率偏差接近±0.5为例，其峰值谱线的两侧谱线在实际中趋近于相等，由于受到噪声的干扰，其值相对于真实值来说出现波动，会造成次高值判定错误的情况，因此，估计误差会出现一个周期性的变化(在本文的仿真条件中，频谱分辨率为3.125 Hz，时间分辨率为0.04 s，归一化是指一个分辨率)。

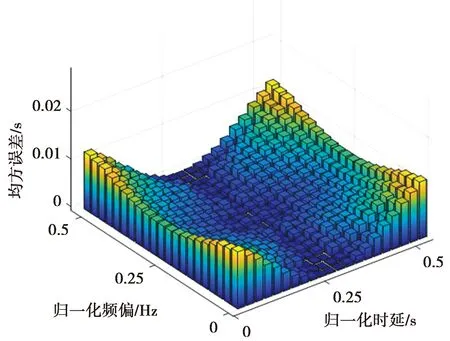
图20 时间估计误差分析

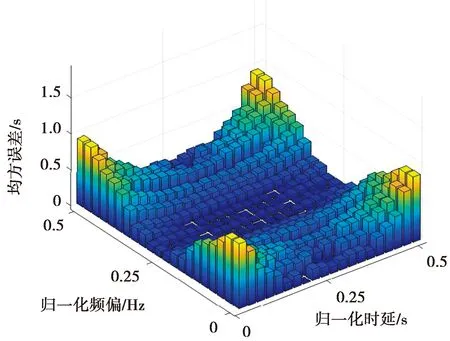
图21 频率估计误差分析

4 结束语

本文提出了一种基于Costas序列的时频联合同步方法，经仿真验证，该方法与基于PN码的同步方法相比，具有更好的抗噪声和频偏能力，可以有效提高短波通信中的捕获率和同步精度，且相同长度下同步性能更好，更加适用于短波通信，可以有效提高恶劣信道条件下的同步性能，为提高短波通信的可靠性奠定基础。