基于人工免疫粒子滤波算法的MIMO-SCFDE 系统信道估计方法

齐永磊，陈西宏，谢泽东

(空军工程大学防空反导学院，陕西 西安 710051)

0 引言

多输入多输出(MIMO)是一种有效的抗多径衰落的技术，研究表明，MIMO系统在不增加系统带宽和天线总发射功率的情况下，可以明显提高系统的抗衰落性能，提高系统的信道容量和频带利用率[1]。单载波频域均衡(SC-FDE)的概念[2-3]由H.Sari等人在1994年提出，SC-FDE借鉴了正交频分复用技术通过频域均衡方法对抗频率选择性衰落的优点，同时保留了单载波信号峰均比低的优势，而且相比单载波时域均衡，在大多径时延时，频域均衡的复杂度明显降低[4-5]。将MIMO技术和SC-FDE技术相结合构成MIMO-SCFDE系统，可以在保证功率高效和抗频率选择性衰落的情况下进一步提高系统数据传输速率。

时变信道估计影响着MIMO-SCFDE系统通信性能，是其关键技术之一。递归最小二乘(RLS)算法、最小均方(LMS)算法和卡尔曼滤波(KF)算法都是经典的时变信道估计算法。相比另两种，KF算法具有更好的性能，但其适用于线性高斯系统[6]，在文献[7]中，Middleton指出，在通信系统中，环境噪声多为非高斯分布，KF算法在此环境中性能不稳定；利用粒子滤波(PF)算法在非线性非高斯环境下估计的优势[8-9]，文献[10—11]分别成功地将经典PF算法用于MIMO系统和SC-FDE系统的时变信道估计，但经典PF算法会带来权值退化的问题，从而影响信道估计的精度[12]；文献[13]将人工免疫的思想引入粒子滤波中，可以有效缓解权值的退化，但其未将此算法应用在时变信道估计中进行研究。本文针对经典PF算法在MIMO-SCFDE系统时变信道估计中出现权值退化的问题，提出了一种基于人工免疫粒子滤波(AIPF)算法的MIMO-SCFDE系统时变信道估计方法。

1 MIMO-SCFDE系统

图1展示了MIMO-SCFDE无线通信系统。此系统发射天线有nT个，接收天线有nR个，对经过映射后的数据进行串/并变换后形成nT个数据流；每个数据流在相应的发射天线上插入循环前缀(CP)后被发送出去，CP的长度必须大于信道最大时延扩展长度L，插入CP后可以使得信道冲激响应和发送信号的线性卷积等效为循环卷积，每个天线上发送数据流的数据帧结构如图2所示。

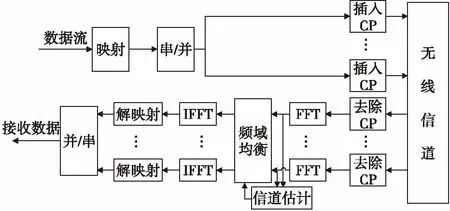
图1 MIMO-SCFDE无线通信系统Fig.1 MIMO-SCFDE wireless communication system

图2 每个发射天线数据流的帧结构
Fig.2 Frame structure for each transmitting

n时刻第t个发射天线上的数据可表示为：

(1)

式(1)中，wt(n)表示P×1的CP向量，dt(n)表示Q×1的数据向量；记K=Q+P。则xt(n)=[xt(n,1),…,xt(n,K)]T，t=1,…,nT。

发射信号进入无线信道，经无线信道传播后被接收端接收，然后去除CP，n时刻去除CP后的接收信号可以表示为：

y(n)=h(n)x(n)+v(n)

(2)

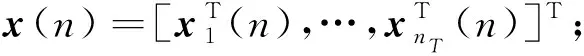
(3)

式(3)中，hr,t(n)表示n时刻第t个发射天线到第r个接收天线的信道冲激响应。

对接收数据进行快速傅里叶变换，FFT长度为Q，由文献[14]知

hr,t(n)=FHHr,t(n)F

(4)

式(4)中，F表示维数为Q×Q的FFT矩阵，矩阵中的元素可以表示为：

(5)

Hr,t(n)为Q×Q对角矩阵，其对角线上的元素为信道冲激响应的傅里叶变换：

(6)

建立系统的状态空间模型是运用人工免疫滤波算法进行信道估计的关键。在MIMO-SCFDE系统中假设每对收发天线间的多径信道相互独立，且多径数目相同。由文献[15]知，可将时变信道建模为一阶自回归(AR)模型，为了减少计算量，只考虑第r个接收天线。

n时刻第r个天线的接收数据可以表示为：

Yr(n)=X(n)Hr(n)+Vr(n)

(7)

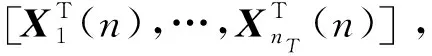
p(zn)=(1-ε)N(0,ξ2)+εN(0,κξ2)

(8)

式(8)中，0<ε<1，N(0,ξ2)的均值为0，方差为ξ2的复高斯分布，表示信道背景噪声；N(0,κξ2)的均值为0，方差为κξ2，表示信道冲激噪声。

对时变信道进行建模得：

Hr,t(n)=aHr,t(n-1)+zr,t(n)

(9)

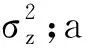
(10)

a=J0(2πfdts)

(11)

J0(·)表示零阶Bessel函数，fd表示最大多普勒扩展频移，ts表示采样周期。将式(9)扩展到矩阵可得下式：

Hr(n)=AHr(n-1)+zr(n)

(12)

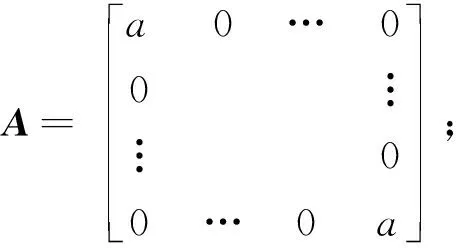
为简化表达，将系统状态空间表达式(7)和式(9)省去r，可以建立MIMO-SCFDE时变信道的状态空间模型，如式(13)所示：

(13)

2 基于AIPF算法的信道估计

2.1 AIPF算法

人工免疫算法模拟了生物的免疫系统，在生物免疫过程中，抗体和抗原起主要作用，人工免疫算法将待求解的问题看为抗原，问题的某个解看作某个抗体，而抗体与抗原的匹配程度用亲和力来描述。通过不断地复制和变异，使得种群抗体亲和力的分布较为均匀，此时的抗体即为最优解。

针对经典PF算法存在的权值退化问题，可以将人工免疫算法与PF算法相结合，依据粒子权值的大小对采样的粒子进行变异处理，然后搜索最优粒子，迫使粒子集合向真实后验分布概率较高的区域移动，从而间接地使取样粒子的建议分布函数和真实后验分布相似。

人工免疫粒子滤波算法的主要步骤如下：

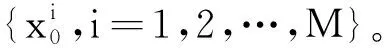
(14)

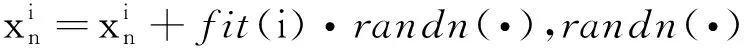
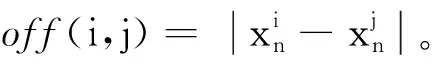
6) 重复步骤3)和步骤4)直到满足某个结束条件。

7) 用最后得到的M个粒子估算出对状态的估计值。

2.2 基于AIPF算法的信道估计实现

本文提出将人工免疫粒子滤波算法应用到MIMO-SCFDE系统信道估计中，以此提高系统信道估计性能。

上文中已经得到MIMO-SCFDE系统的状态空间表达式以及AIPF算法的步骤，将利用AIPF算法进行信道估计的具体步骤总结如下。

步骤1)信道估计的初始化：

步骤2)从建议分布函数中采样：

步骤3)当有新的观测值时，通过观测方程对权值进行更新：

步骤4)计算每个抗体的亲和力以及抗体和抗体之间的排斥力：

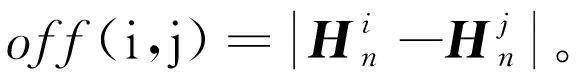
步骤5)克隆抗体，依据每个抗体的亲和力对抗体进行克隆操作。

步骤6)变异：

步骤7)选优：

将变异后所有抗体的fitn(i)和offn(i,j)计算出，抛弃offn(i,j)<0.000 1中的一个抗体，并按fitn(i)进行排序，选出前面的M个抗体更新记忆单元，返回步骤4，直到满足终止判据为止。

步骤8)重采样：

步骤9)状态估计输出：

当n=n+1，返回步骤2)。

3 仿真结果与系统性能分析

用Matlab对所用算法进行仿真，采用2发2收天线，V-BLAST空时发射方案；频率选择性衰落与时间选择性衰落同时考虑在内，参数由Jakes模型产生；归一化多普勒衰减率fdts分别取为0.005，0.01和0.02，对应不同时变程度的信道；信源调制方式为QPSK，采样的粒子数M=50。

图3和图4分别表示fdts取0.005，0.01和0.02时本文信道估计算法分别在加性高斯白噪声和Middleton-A噪声环境下的误码率(BER)性能。

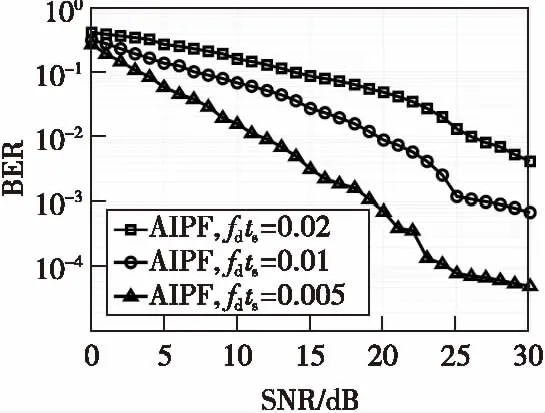
图3 AWGN环境下，AIPF算法在不同fdts下BER比较Fig.3 The BER comparison of AIPF in different fdts when in AWGN envirenment

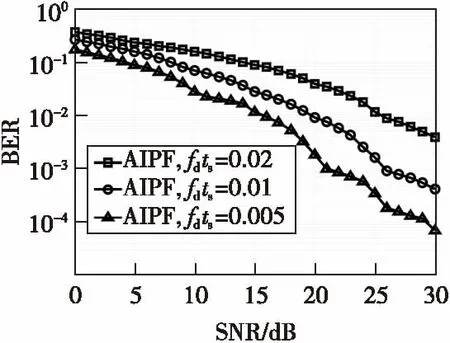
图4 Middleton-A噪声环境下，AIPF 算法在不同fdts下BER比较Fig.4 The BER comparison of AIPF in different fdts when in Middleton-A noise envirenment

由图3、图4可以看出，当归一化多普勒衰减率增加即信道时变程度加剧时，系统BER增加，估计的精度降低。而图4相比图3，并没有显著变化，说明本文算法在非高斯分布噪声环境下具有较好的顽健性。

fdts取0.01时，将本文算法，LS算法，Kalman滤波算法以及PF算法分别在AWGN和Middleton-A噪声环境下应用于MIMO-SCFDE信道估计中，将其仿真结果进行比较。其BER性能和归一化均方误差(NMSE)如图5—图8所示。

图5和图6展示了在AWGN环境下四种信道估计算法的BER和NMSE，图7和图8展示了在Middleton-A噪声环境下四种信道估计算法的BER和NMSE。可以看出，无论在哪种环境下进行时变信道估计，本文算法的BER性能和NMSE性能均好于其他三种算法。在Middleton-A噪声环境，即非高斯分布噪声环境下，用Kalman滤波算法进行时变信道估计时，其BER和NMSE性能不稳定，低于处在加性高斯白噪声环境下的性能，说明Kalman滤波算法在非高斯分布噪声环境下顽健性较差，而粒子滤波算法和本文算法均未受影响。

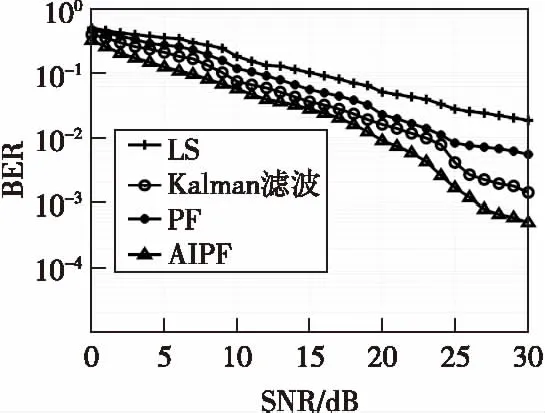
图5 fdts=0.01时，AWGN噪声 环境下四种算法BER比较Fig.5 The BER comparison among the four algorithms with fdts=0.01 when in AWGN noise environment

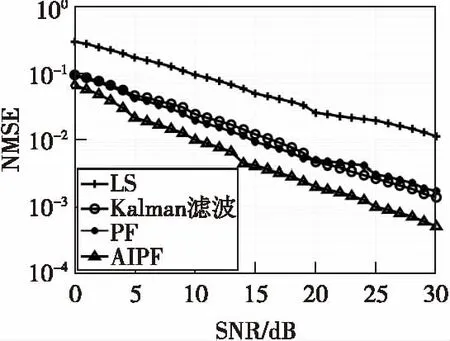
图6 fdts=0.01时，AWGN噪声 环境下四种算法NMSE比较Fig.6 The NMSE comparison among the four algorithms with fdts=0.01 when in AWGN environment

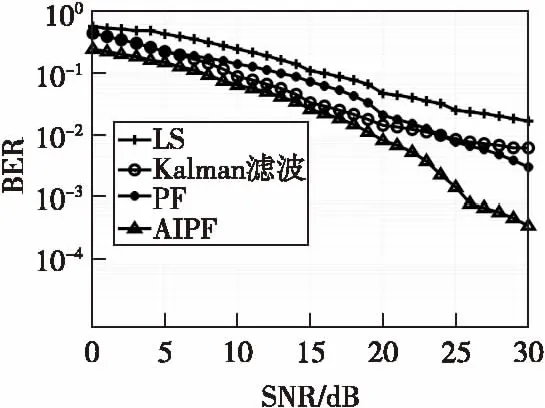
图7 fdts=0.01时，Middleton-A噪声 环境下四种算法BER比较Fig.7 The BER comparison among the four algorithms with fdts=0.01 when in Middleton-A noise environment

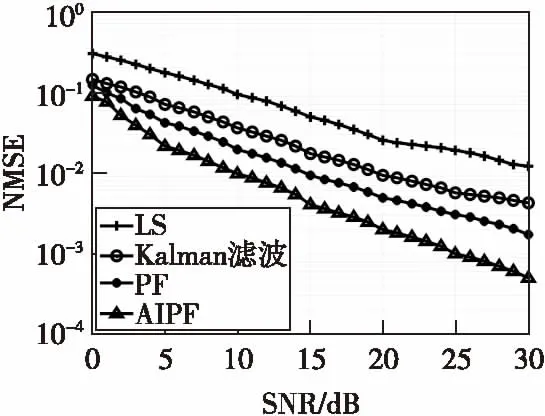
图8 fdts=0.01时，Middleton-A噪声 环境下四种算法NMSE比较Fig.8 The NMSE comparison among the four algorithms with fdts=0.01 when in Middleton-A noise environment

4 结论

本文提出了基于AIPF算法的MIMO-SCFDE系统时变信道估计方法。该方法将人工免疫的思想引入到PF算法中，有效缓解了PF算法权值退化的问题，提高了信道估计的精度。仿真结果表明，相比LS算法，Kalman滤波算法以及经典PF算法，AIPF算法在高斯分布噪声环境以及非高斯分布噪声信道环境下均可以得到较低误码率(BER)以及归一化均方误差(NMSE)，而且在非高斯分布噪声环境下具有较好的顽健性，可以有效提高MIMO-SCFDE系统信道估计的性能。但AIPF算法过程较为复杂，如何在保持其性能的基础上降低算法复杂度是下一步研究方向。