起重机长细臂架结构应力解析法的适用性

王 欣,范雯霖,顾迪民

(1.大连理工大学 机械工程学院,辽宁 大连 116023; 2.哈尔滨工业大学 机电工程学院,哈尔滨 150001)

随着制造工艺的提高和高强度合金钢材的应用,桁架臂结构如塔式起重机、履带起重机、全地面起重机等朝着高耸化、轻柔化、大长细比方向发展[1-2].对于这种大长细比的桁架臂而言,由于强度高、截面小,相对于强度破坏,更易受压受弯而失稳破坏,因而采取合理的计算方法进行应力与位移计算非常必要[3].

目前,企业大多根据GB/T 3811—2008《起重机设计规范》[4]中给出的解析计算方法来进行结构的设计与计算,但规范中也提出,当有必要做更为详细和精细计算时,可采用积分法、逐步逼近法及有限元法进行非线性分析.显然,规范中给出的解析法具有一定应用范围与要求.而随着结构的长细比加大,结构的非线性越来越明显,现行的解析法是否能继续适用,需要深入分析与对比[5].为此,本文对解析法的计算原理进行阐述,对比有限元法,结合实例分析其适用性.

1 计算原理

1.1 力学分析

履带起重机臂架是典型的桁架臂结构,目前产品的臂架长度达百米级[6],结构材料强度级别达800 MPa以上,臂架长细比超出100,其应力分析成为业内关注热点,也是对规范中解析法的挑战.本文以750 t履带起重机主臂为研究对象,如图1所示,分析不同臂长不同幅度下结构应力的变化情况.

图1 750 t履带起重机结构示意图Fig.1 Boom structure of 750 t crawler crane

进行力学分析，主臂为空间桁架结构,所受载荷也是空间的[7].因此,转换为变幅和回转的两个平面进行力学分析.

在变幅平面内,如图2(a)所示,主臂根部与转台铰接,头部与变幅拉板铰接,可认为是两端简支构件.受自重、起升载荷、起升绳载荷及变幅拉板载荷作用,当臂架头部起升载荷和变幅拉板载荷作用点不同时,两者所构成的合力即臂架轴向力,不一定完全指向臂架轴线,会由此带来弯矩作用.因此,在受力分析时,要特别考虑到铰点位置不重合带来的附加弯矩作用.由于臂架自重和可能存在的头部附加弯矩作用,使得臂架在两端简支状态下有轴向力和弯矩的共同作用,称之为压弯构件.

在回转平面内,如图2(b)所示,主臂根部与转台为固支约束,头部变幅拉板的载荷有阻止臂架侧向位移的作用,具有一定柔性约束作用,但通常简化为自由端,由此可看作为一端固定一端自由的悬臂结构.与此同时,臂架会受到重物偏摆而带来水平载荷和风载荷的作用(风侧向吹对结构更为不利),导致结构越靠近根部,故受到水平载荷引起的弯矩越大.与变幅平面结合,臂架实质是双向压弯构件.

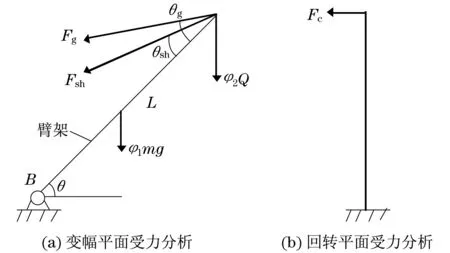
图2 臂架变幅平面受力分析模型Fig.2 Mechanical analysis model of boom in

1.2 解析法计算原理

通过上述受力分析,在进行解析计算时,根据结构刚度进行线性和非线性两种方法分析.对于刚度较大的结构,即臂长较短、长细比较小时,结构的变形相对小,适用于小变形理论的计算.因此,可采用线性分析(也称强度分析、一阶分析)方法来计算结构应力[8]，即

(1)

式中:N为臂架轴向力;A为截面面积；Mx和My为臂架在两个平面内的弯矩;Wx和Wy为臂架截面在两个平面内的抗弯模量;[σ]为臂架材料许用应力.

当结构长细比较大时,结构表现出明显柔性,会因弯矩作用产生变形,轴向压力作用会进一步引起附加弯矩的产生,从而导致变形增加,构成大变形大位移结构,形成几何非线性[8].这种情况下,变形前后的应力显然是不同的,变形后的应力才是结构真实应力的表现.解析法是通过能量理论推导并做一定简化而得到的,以稳定性系数和放大系数来体现大变形带来的应力影响.稳定性系数与结构长细比相关,长细比越大,稳定性系数越小.放大系数与轴向力、临界载荷比值相关,比值越小,即轴向力越接近临界载荷,放大系数越大,产生的附加应力越大.

由此,在解析计算中,首先要计算出结构的长细比和临界载荷.长细比考虑了不同约束、不同截面尺寸带来的变化[9]，即

(2)

式中:μ1为与约束条件有关的长度系数;μ2为与截面变化有关的长度系数;μ3为与变幅拉板载荷的约束有关的长度系数;lc为计算长度；r为臂架截面的回转半径.

对于桁架结构,还会考虑剪切变形引起的长细比变化,用换算长细比来表示，即

(3)

式中:A为截面弦杆面积之和;A1为所截截面的腹杆面积之和.

临界载荷的实质为仅受轴心压载荷时的临界失稳值

(4)

式中：E为弹性模量.

变形后的应力即是非线性应力,也称为稳定性应力或二阶应力.为方便计算,采用二阶理论进行推导,得到的是非线性的近似解,即

(5)

式中:φ和ψ分别为整体稳定性系数、稳定性修正系数;αx和αy分别为两个平面内的弯矩放大系数.

(6)

1.3 有限元计算原理

有限元计算通常将结构划分成有限个单元,对各单元进行力学分析,建立各种单元矩阵,通过求解矩阵,获得结构的应力与位移.目前商用有限元软件已很成熟,可以计算结构线性与非线性应力.由于结构可以划分得足够小,可用有限数量的未知量去逼近无限未知量的真实系统,保证相应的计算精度,达到计算更为准确的目的.

本文应用Ansys有限元软件进行臂架结构建模,应用软件提供的线性和非线性方法，计算结构的应力与位移,并与解析计算结果对比,分析解析结果的合理性与适用性.

臂架结构的有限元模型如图3所示,这里不仅建立了臂架有限元模型,还建立了变幅拉板有限元模型,并与臂架结构耦合连接,更真实地反映出两者的相互影响关系.建模时,臂架弦杆与腹杆采用beam188梁单元,拉板采用link180杆单元.在变幅拉板末端施加全位移约束,在臂架根部铰点处施加静定的位移和角位移约束.臂架自重按杆件的布置由模型自动考虑,起升载荷施加在与起升滑轮轴连接的节点处,同时按Qtan2°施加水平侧载.

图3 臂架结构有限元模型Fig.3 Finite element method of boom

2 计算结果对比分析

选取750 t履带起重机的3种臂长(中长臂、长臂和最长臂)和3种幅度(最小幅度、中等幅度和最大幅度)共9组工况进行临界载荷、线性和非线性应力的计算.

表1～表3是结构临界载荷关于解析法和有限元法的结果对比.可以看出,两种计算数值还是存在一定差异的.当臂架幅度较小时,回转平面的解析值大于有限元值,超过的最大幅值在8.2%.随着幅度增加,回转平面与变幅平面的解析值均小于有限元值,低于的最大幅值在-10.7%.

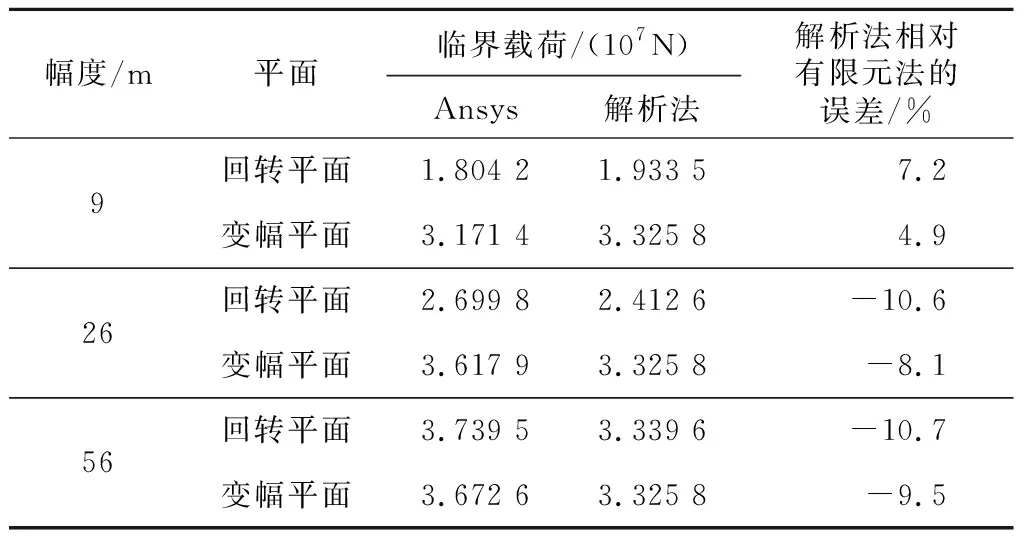
表1 63 m主臂临界载荷结果对比Tab.1 Comparison of 63 m boom critical load

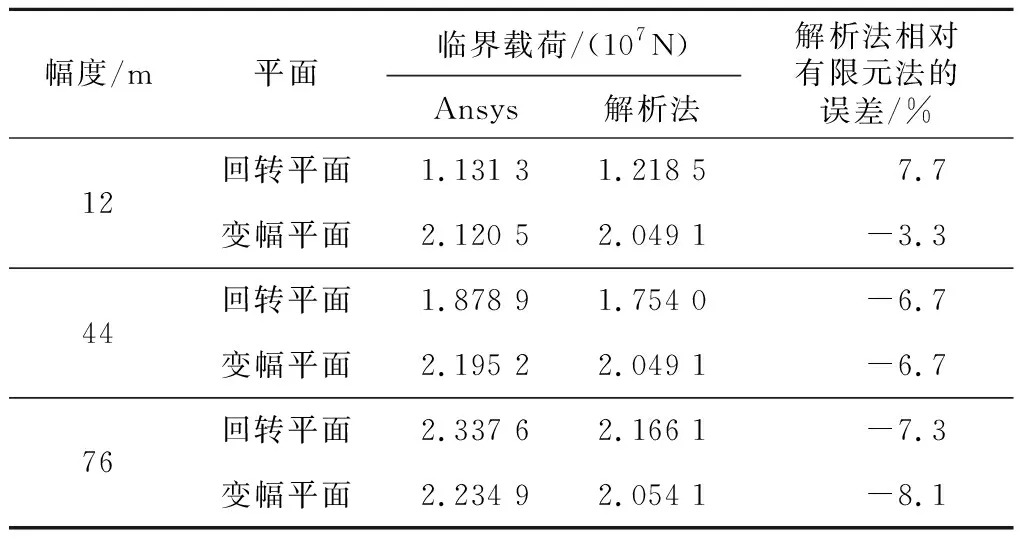
表2 84 m主臂临界载荷结果对比Tab.2 Comparison of 84 m boom critical load

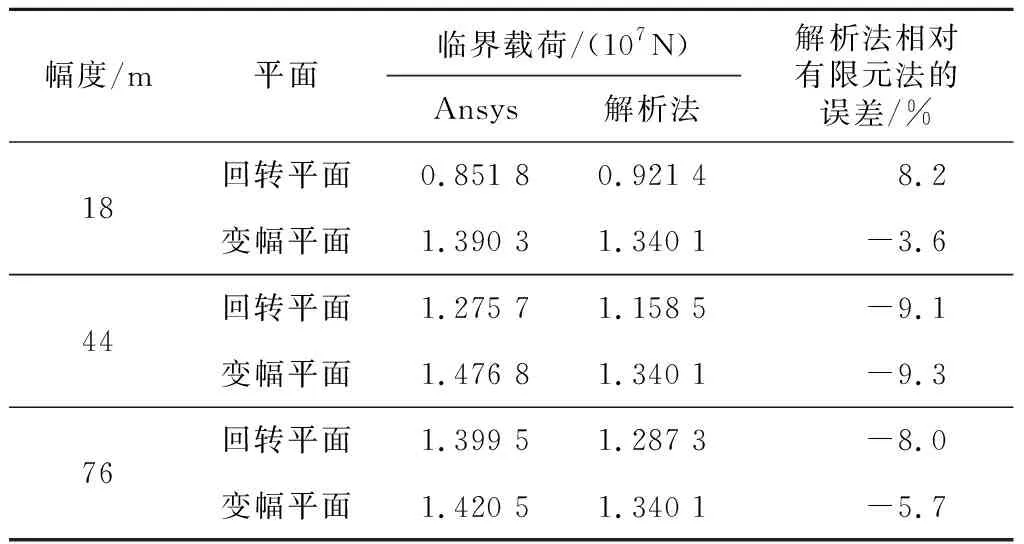
表3 105 m主臂轴向临界载荷对比Tab.3 Comparison of 105 m boom critical load

解析值与有限元值的误差先高后低，形成的原因如下:

(1) 变幅拉板对臂架结构的约束问题.臂架头部与变幅拉板连接,在回转平面起对臂架侧向位移约束的作用,但这种约束不是刚性约束,与变幅拉板载荷大小有一定关系,属于柔性约束.幅度大,变幅拉板载荷大,对臂架回转平面的位移约束作用也大,从而使得临界载荷有所增加.解析法对这种因载荷变化的约束方式是采用长度系数μ3计算,但难免存在计算上的简化,致使临界载荷计算结果存在或多或少的误差.而有限元中,是直接进行变幅拉板与臂架结构耦合连接建模,计算结果更符合实际.

(2) 换算长细比问题.众所周知,临界载荷与长细比有很大关系.桁架结构这种杆系结构,承受剪切载荷的能力不如实腹式结构,会产生较大的剪切位移,临界载荷也会有所降低.解析法是通过换算长细比来考虑剪切位移对临界载荷的影响,为方便计算,对计算公式进行了一定简化,这使得计算结果必然存在误差.有限元是直接将弦杆和腹杆按实际几何关系来建立,真实体现剪切位移对临界载荷的影响.

由此可以看出,结构的组成形式与边界条件对临界载荷的计算影响是较大的.因此,当用解析法时,对结点可否简化处理宜视结构实际工作情况而定.临界载荷的计算误差,必然导致非线性应力的计算误差.

表4～表6是主臂线性应力和非线性应力的对比.可以看出,线性应力方面,解析值与有限元值很接近,表明解析法在线性计算方面是可行的.对于尚存在的细小差异,要注意拉板与臂架端部连接的构造方式,即变幅拉板铰点与起升载荷铰点、臂架轴线不重合带来的附加弯矩、应力变化,这在解析计算中是不能忽略的.

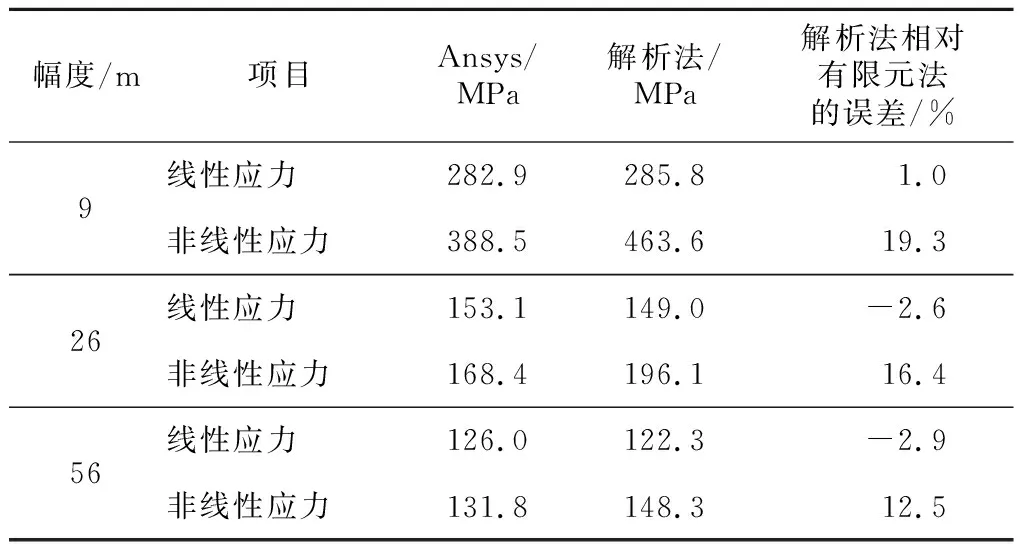
表4 63 m主臂解析计算与Ansys计算应力对比Tab.4 Comparison between theoretical method and

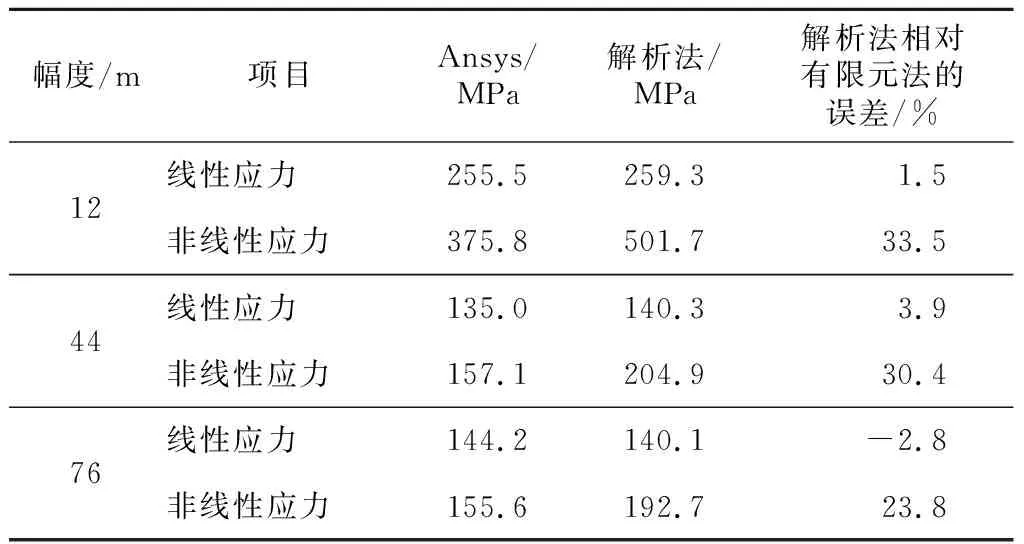
表5 84 m主臂解析计算与Ansys计算应力对比Tab.5 Comparison between theoretical method and

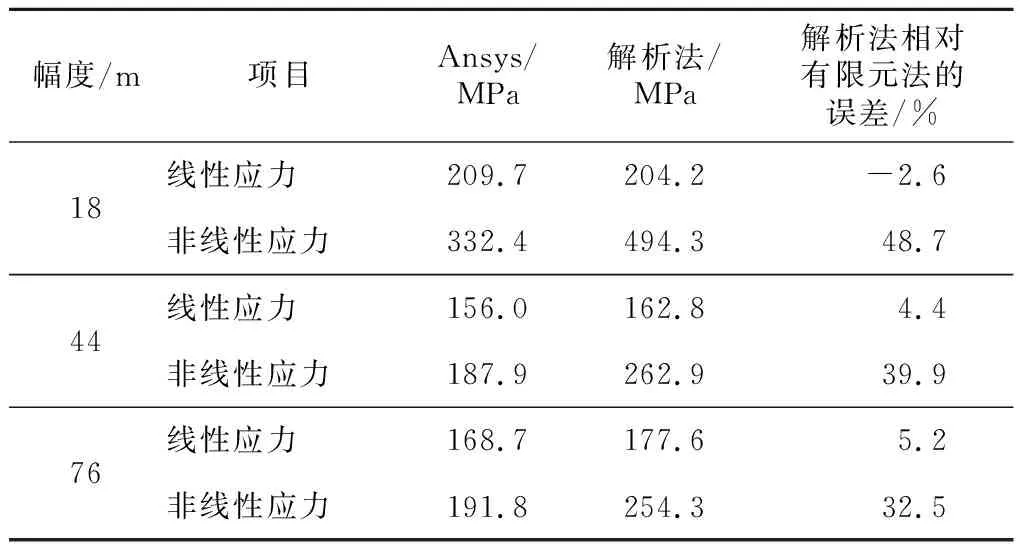
表6 105 m主臂解析计算与Ansys计算应力对比Tab.6 Comparison between theoretical method and

非线性应力方面,相同臂长,幅度越小,解析值高出有限元值的差值越大;不同臂长小幅度下,臂长越长,解析值高出有限元值的差值越大,在19.3%～48.7%.除了临界载荷的简化计算问题外,还可能源于变形放大系数的计算方法.参考国外有关设计规范,文献[10]指出带有弯矩增大系数的线性弹性分析(即“近似非线性分析的解析法”),弯矩增大系数不得大于1.4.弯矩增大法通常保守,对于二阶效应高的结构不适用.文献[11]指出用二阶系数(即增大系数)增大线性分析结果的方法来模拟非线性效应也是可用的.此近似非线性分析法可作精确非线性分析法的一个替代,用增大线性分析内力代表结构中的非线性效应.但指出其适用条件:结构的非线性侧向位移与最大的线性位移比等于或小于1.5(亦即非线性效应高的结构不适用).说明对于大长细比结构,近似非线性解析算法依然有较大的局限性,其计算公式值得进一步商榷.

就有限元的计算结果来看,非线性应力与线性应力差别较大,尤其是臂架越长,两者差异越大,小幅度时更为明显,最大可达48.7%.由于小幅度时,起重量相对较大,水平侧载(Qtan2°)也比较大,导致位移较大,非线性更为明显.故在大臂长、大长细比下,必须进行非线性应力分析.而解析法的非线性应力分析是依据二阶理论推导的,是近似非线性算法,从计算结果来看,有一定的保守性,幅度小时情况更为明显.当然也存在有关系数选取上是考虑了制造加工等误差而进行一定放大等因素,但总的来说,不完全适用,需要进一步的修正与改进.

3 结论

通过对750 t履带起重机主臂的解析计算与有限元计算分析对比,可以看出：长细臂架的非线性特征已很明显,应采用非线性应力分析替代线性应力分析.当前的解析法不完全适用于长细臂架的非线性应力分析,尤其在临界载荷与放大系数法方面,需要进一步的修正与改进.因此，宜采用更为精细的非线性有限元法分析.