基于超声振动加工变幅杆的优化设计
张德琪,沈景凤,陈俊豪
(200093 上海市 杨浦区 上海理工大学 机械工程学院)
0 引言
超声振动加工技术是一种重要的特种加工技术,在航天领域、国防领域以及医疗等领域发挥着越来越重要的作用,解决了许多难加工材料的精密加工问题[1]。超声波振动系统一般由超声波发生器、换能器、变幅杆和加工工具组成。由于换能器端面上的振幅微小于10μm,需要在换能器端面连接变幅杆,以实现振幅放大。变幅杆是超声振动系统中最为重要的组成部分,合适的变幅杆可以显著提高加工效率与加工工件质量。变幅杆一般有单一型和复合型两种类型[2]。在高强度超声加工工艺中,往往要求变幅杆末端必须具有较大的振幅,而变幅杆的形状因素和放大系数是影响振幅的主要因素,所以要求这两个值越大越好,而单一变幅杆一般此优彼劣,很难二者兼顾,因此需使用各种复合型或者形状复杂程度高的变幅杆。目前,由多种母线组合而成的复合型变幅杆在精确设计及工作稳定性方面仍存在较多缺陷[3]。本文基于波动理论来设计加工圆锥型复合变幅杆,并导入SolidWorks 中进行有限元分析,利用优化算例可以较好地改善以往由多种母线组合而成的复合型变幅杆在设计和工作方面的不足。
1 变幅杆的功能
1.1 变幅杆的类别
变幅杆根据不同的分类方法可以分成图1 所示的类型。

图1 变幅杆分类图Fig.1 Classification of horns
变幅杆是组成超声振动振动系统的关键部件,由于换能器产生的振幅特别小,一般在几微米左右,但超声加工需要几十微米的幅度,所以需要变幅杆将振幅放大,完成加工[4]。变幅杆的作用有负载阻抗匹配和聚能。作为负载时,将振动的机械能传递给工具,最终工具迫使工件振动,从而完成去除材料的加工;作为聚能作用时,能量密度和振幅存在式(1)的关系:

式中:K——常数;J——能量密度;A——振动的幅度。由此定性分析二者关系,变幅杆振动幅度与面积大小成反比,所以变幅杆一般为上面直径大、下面直径小的结构,同理,圆柱结构可以实现振动等幅度传递。
1.2 变幅杆的设计
1.2.1 理论分析
国内目前对于变幅杆的设计理论大多都是建立振动方程,利用一些边界条件求解出变幅杆的频率方程,这样计算出的变幅杆结构简单,但是当改变变幅杆一些结构时对变幅杆的影响较大,没法计算改变结构后的具体数据。针对这种情况,本文采用了先用变幅杆理论计算出具体数据,然后用SolidWorks 建立模型,并建立与实际一样的三维模型,包括螺纹孔。利用SolidWorks 的优化算例,分析出比较合理的尺寸分布,最后通过谐响应分析得到优化后的变幅杆,完成优化设计。
根据设计旋转超声振动电加工机床的需求,决定采用圆锥复合型变幅杆,这种变幅杆放大性能好,工作稳定,受力状况好。下面简单阐述圆锥复合变幅杆的理论计算[5]。
如图2 所示,以圆锥复合变幅杆大端与圆锥交界处为节点位置,建立坐标轴,将变幅杆大端、过渡部分和小端分别称作第1、2 和3 部分。假设变幅杆为理想状态,则振动方程为

图2 圆锥复合变幅杆Fig.2 Cone composite horn

式中:ξ——质点的位移函数;k——圆波数;S——截面积。
由于设计的变幅杆为半波长类型,所以k=k,根据振动方程可以得到圆锥复合变幅杆的小端质点位移分布函数
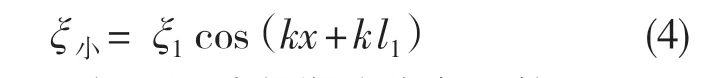
中间圆锥过渡段的质点位移分布函数
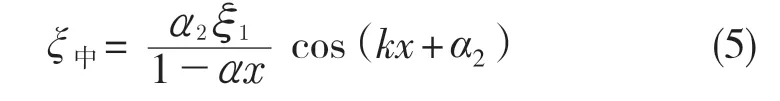
复合变幅杆大端部分质点位移分布函数

式中:l1,l2,l3——圆锥复合变幅杆各段长度;锥度系数为α=(N-1)/(Nl2);N——大端与小端的直径比。
得到整个圆锥复合变幅杆的频率方程:

位移节点为
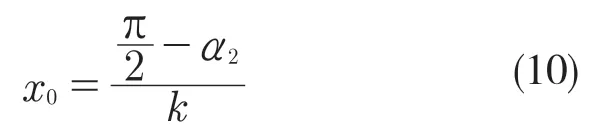
放大系数Mp为

1.2.2 变幅杆的设计
变幅杆需要与换能器的前盖板紧密连接,为了更好地传递振动,减少能量损失,设计的变幅杆大端直径应该和换能器前盖板直径一样大[6],所以变幅杆大端直径为50 mm;设计的变幅杆类型为1/2 波长圆锥复合型,即l1=l3。为了方便计算变幅杆的数据,给定l2的尺寸为50 mm;材料选用传声性能好,价格便宜且易加工的45 号钢,其纵波声速c=5 170 m/s、密度ρ=7.85 g/mm3、杨氏模量E=211 GPa、泊松比λ=0.28。
查阅资料,面积比N=2 时变幅杆性能相对较好[7],故以N=2 计算。将已知数据代入式(9)得l1=l3=44.1 mm。联立式(2)、式(3),计算节点位置x0=17.4 mm,注意节点位置相对于坐标原点开始,由式(11)计算出放大倍数Mp=3.469 8。圆锥复合变幅杆的初步尺寸如表1 所示。

表1 圆锥复合变幅杆计算尺寸Tab.1 Calculated size of cone composite horn
这样就完成了圆锥复合变幅杆的理论计算,变幅杆的尺寸全部确定。接下来,结合频率分析和谐响应分析来优化初步设计的变幅杆,优化设计出性能接近真实的圆锥复合变幅杆。
2 变幅杆的优化
2.1 计算的变幅杆模态分析
根据理论计算出来的数据进行SolidWorks 建模,然后进行圆锥复合变幅杆的模态分析。由于理论计算是无约束条件下的频率方程,在频率分析时不添加任何约束,材料设置为45 号钢,网格采用自动生成,利用FFEPlus 求解前15 阶频率,发现在12 阶时最接近设计频率,为19 631 Hz。查看其12 阶振型,发现共振变形为变幅杆为纵振状态,可以满足变幅杆纵向振动加工的需求[8],具体分析如图3 所示。
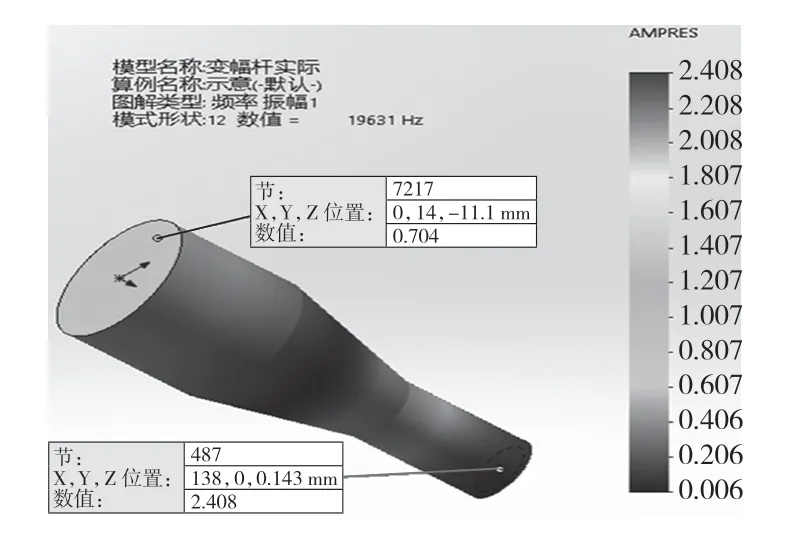
图3 理论圆锥复合变幅杆模态Fig.3 Theoretical cone composite horn mode
对计算的理论变幅杆进行分析,频率误差为(20 000-19 631)/20 000=1.845%,由大端面和小端面的相对位移计算放大倍数MP=2.408/0.704=3.420,则放大倍数误差为(3.469 8-3.420)/3.469 8=1.397%。通过分析计算,可知理论计算符合设计要求,但这只是简单结构下的结论。变幅杆往往需要通过法兰跟机床连接,在变幅杆底部还需要与加工工具连接,这些结构对变幅杆的谐振频率有影响,尤其法兰盘的大小会影响变幅杆的放大状态[9],对于法兰盘和加工工具目前没有较好的计算方法。利用SolidWorks 的优化算例对实际变幅杆进行优化分析,最后进行谐响应分析,得到最终实际性能优越的变幅杆。
2.2 变幅杆的优化
根据旋转超声系统的结构,确定变幅杆的法兰盘大小,并将其定位在计算的节点位置。法兰盘直径100 mm,在72 mm 处有4×Φ4 的安装孔,重建变幅杆模型。完成建模后,为了得到更加实际的工作状态,将变幅杆法兰盘处添加固定约束,然后进行模态分析,找出最接近20 000 Hz 的模态,发现在第10 阶模态达到20 587 Hz,并且变幅杆属于纵向振动状态[10],具体如图4 所示。

图4 变幅杆优化前的模态Fig.4 Modal before optimization of the horn
打开SolidWorks 的设计算例,建立并设置频率传感器,频率传感器可以获取到变幅杆在第10阶振型下的共振频率。以变幅杆的大端、过渡段、小端的长度为变量,结合变幅杆优化理论,给定过渡段范围为40~50 mm、大端和小端的长度为40.1~48.1 mm,进行优化算法。
经过算法优化分析,得到表2 中的优化结果。变幅杆尺寸确定后,只需要进行变幅杆的谐响应分析,看是否满足设计的需要。
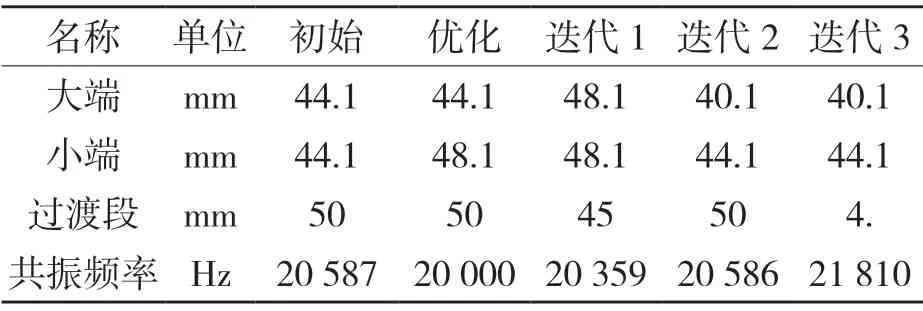
表2 优化结果和部分优化数据Tab.2 Optimization results and partial optimization data
2.3 优化后变幅杆的谐响应分析
优化设计的圆锥复合变幅杆带有法兰盘,由于法兰盘的存在,使得变幅杆工作端的振幅变小。为了确保放大倍数,进行变幅杆谐响应分析,设置求取20 000 Hz 附近的10 阶模态,搜索范围在10 000~25 000 Hz。按照实际工作状况固定变幅杆法兰盘,给变幅杆大端一个统一基准的0.01 mm的激发位移,网格选用带有曲率的网格化分,曲率网格可以使谐响应分析的结果更加可靠[11]。分析完成后列举共振频率,在求出的各阶振动频率中,第6 阶频率为20 012 Hz,最接近设计的理论值20 000 Hz,误差不超过1%,满足设计和理论的需要,列举的共振频率如表3 所示。

表3 共振频率Tab.3 The resonant frequencies
变幅杆在第6 阶振型下共振频率为20 012 Hz,其振型图如图5 所示。通过分析图5 可以看出,在换能器与变幅杆连接处,换能器给其0.01 mm振幅位移;在法兰盘处的变形最小,变幅杆可以输出0.039 mm 振幅位移,从而完成放大的功能,完成超声加工。

图5 变幅杆优化后谐响应分析Fig.5 Harmonic response analysis after horn optimization
由变幅杆谐响应图6 可知,在20 012 Hz 时优化后的变幅杆发生共振,并且振幅情况在整个响应频率中较大,在40μm 左右,可以正常完成超声加工,且性能良好。
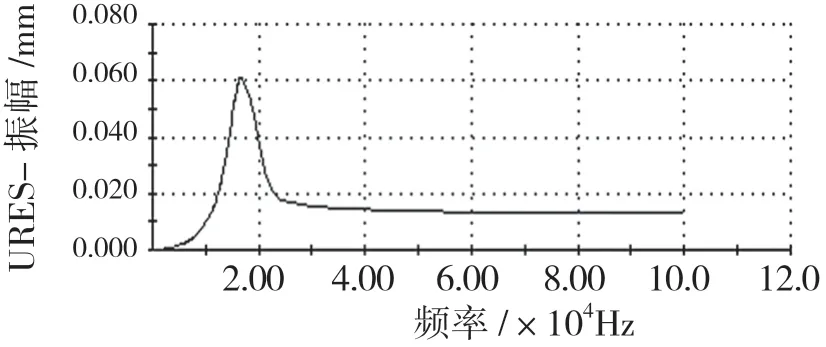
图6 优化后变幅杆频率响应图Fig.6 Frequency response diagram of the horn after optimization
3 结语
本文通过分析,确定了变幅杆的类型为圆锥过渡复合结构。从理论计算了基本尺寸,并从具体的结构出发,建立了变幅杆的三维模型,考虑了法兰盘和螺纹孔对变幅杆的影响。利用SolidWorks 进行模态分析后,确定了优化变量,利用SolidWorks 的优化算例优化了变幅杆的具体尺寸,并通过谐响应分析证明了优化后的变幅杆性能稳定。所优化设计的变幅杆能够满足超声加工的需要,性能可靠,可以满足实际工程需求。

