多孔介质粗糙表面分形-蒙特卡罗传热研究
徐静磊,张赛,王昌进,张杰,高伟业
(650500 云南省 昆明市 昆明理工大学 机电工程学院)
0 引言
多孔介质是一种强化传热介质[1-3],被广泛应用于建筑、食品、化学品、煤炭、石油开采油气贮藏、热管虹吸材料、化工床、航空航天复合材料、人体和动物的组织器官、植物体内的水分和营养运输系统等诸多领域,因此研究多孔介质的传热在许多领域都具有重要的意义[4-7]。
由于多孔介质具有自相似性,其任何表面,在微观层面看来都具有大量的凸凹和几何缺陷而显示出粗糙的形态,即绝对光滑的表面是不可能存在的。对于固体表面,无论其表面是如何的形成方式,都不会是规则的,其高度在某一水平面来回波动。那些高度高出平均几何平面的称为微凸体,低于这个平面的称为凹坑[8]。粗糙表面对于研究摩擦、辐射、导热、导电、黏附及流体的流动传热都有相应的影响,因此研究粗糙表面的传输机理,对于许多学科和领域都有很重要的意义[9]。
Shishkina O[10]等对粗糙形状为矩形的边界进行了模拟研究,研究结果表明,冷热板在粗糙形态下的边界层厚度要明显大于光滑表面,原因是粗糙单元间的间隙对流传递存在阻碍作用,所以传热不仅不会增强,甚至会出现减弱。Wei Ping[11]等对不同的粗糙壁面进行了研究,结果表明,当上下表面都为粗糙表面时,传热效果会现增强,但当上下两板依次为光滑表面与粗糙表面时,传热基本不发生增加。丁雪兴[12]等针对干气密封非稳态下的摩擦特性对密封性能的影响进行了研究,建立了三维粗糙实体与理想光滑刚体滑动摩擦热力耦合模型。发现粗糙表面最高接触温度随滑动时间增加呈逐步上升趋势,并且温度呈现一定的波动性。
近些年关于接触热导,很多学者进行了大量的实验研究[13-15]。理论上,人们主要研究接触表面的微观接触状态和形式,简化成单点接触模型,然后根据材料特性和热阻定义等进行求解。
虽然目前存在许多研究方法,但大部分学者研究的是粗糙表面与传热热阻的关系,很少有人研究粗糙表面和传热系数之间的关系。本文基于分形-蒙特卡罗法研究传热系数与微凸体及孔隙率之间的关系。避开了传统热的模拟热阻法,减少了经验常数的使用,运用分形理论使得结果更接近真实情况。
1 关于蒙特卡罗法的模型建立
为了研究粗糙表面的具体形貌和内在机制,就要刻画出粗糙表面的分形特征,描述多尺度下的结构。Majumdar 和Mandelbrot 提出的W-M 分形函数进行修正得到了M-B 模型,粗糙表面的二维模型表达式如下[16]:
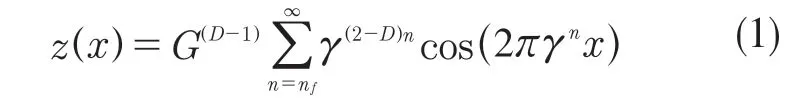
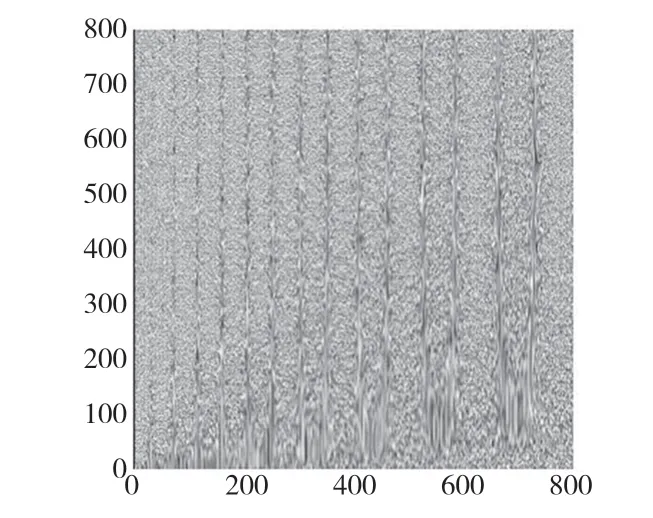
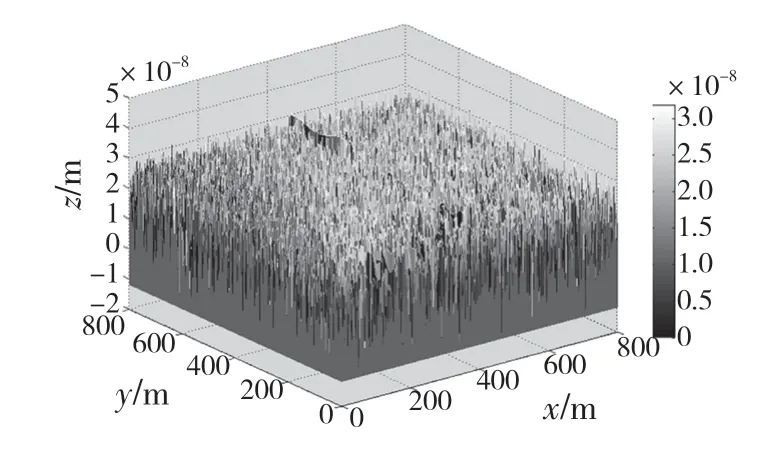
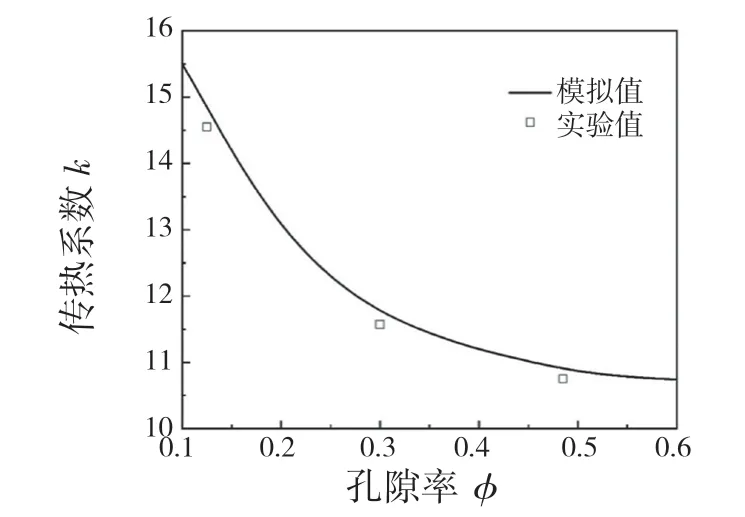
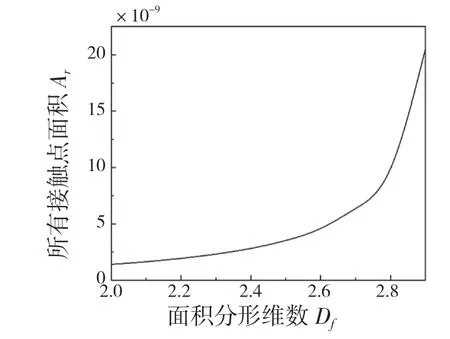
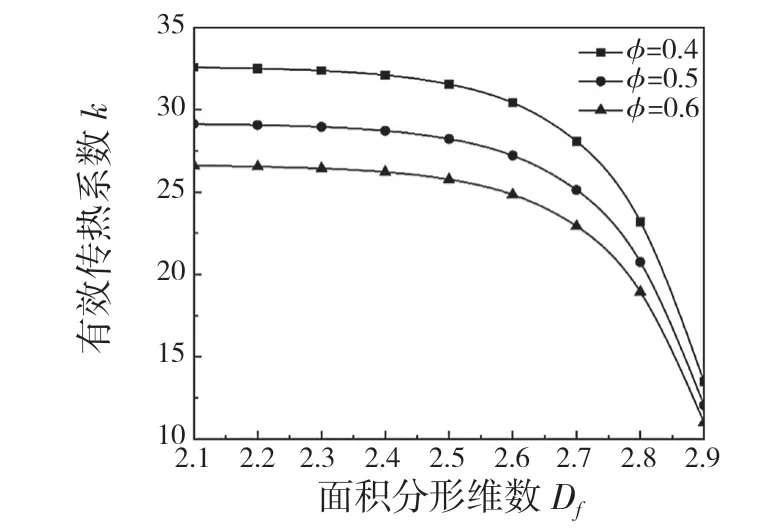
式中:z(x)——粗糙表面轮廓幅值函数;x——测量坐标。此处,D——表面轮廓分形维数,(1 式(1)具有连续性、处处不可微和自仿射性,能满足粗糙表面轮廓曲线的所有特性。 通过式(1)得到的粗糙表面垂直剖面的二维模型仿真图如图1 所示。通过该图可以看出粗糙表面的二维剖面轮廓,该轮廓线能够很好地符合粗糙表面的特性,即处处连续、不可微、自仿射性。通过放大局部轮廓,可以看出粗糙表面在任意一个长度尺寸下都是不平滑的。 图1 二维粗糙表面剖面模拟图Fig.1 2D rough surface profile simulation 对于粗糙表面的三维模型图也存在相关的蒙特卡罗表达式[17],如式(2): 式中:M——曲面褶皱重叠数;φm,n——随机相位(0 ≤φm,n≤2π);n1——最低空间频率序数,n1=0;nmax——最高频率序数,nmax=int[lg(L/Ls)/lgγ];Df——面积分形维数(三维空间2 图2、图3 是通过MATLAB 仿真得到的三维模型图。图2 为关于x-y 轴方向的正视图,分别在x,y 轴方向设置了800 个点,每两个点之间间距为1 nm;图3 是一般视角看到的三维图,此处在z 轴方向设置的粗糙表面上微凸体高度取值在3.2×10-8m 左右,图3 中颜色深浅代表微凸体在x-y 面内的面积大小,占据面积越大颜色就越重,微凸体尖端的x-y 截面的面积较小,所以颜色较浅。由图3 可知三维蒙特卡罗法能够显示出粗糙表面的表面轮廓,与真实粗糙表面很接近。 图2 三维粗糙表面关于X-Y 方向的正视图Fig.2 Elevation view of 3D rough surface in X-Y direction 图3 三维粗糙表面仿真Fig.3 3D rough surface simulation 多孔介质表面的微凸体是随机分布的,可以把分形理论与蒙特卡罗方法结合起来,研究多孔介质粗糙表面的传热特性。 由关于微凸体分布的概率密度函数[18-19] 式中:λ——微凸体直径。 其中f(λ)≥0,λmin≤λ≤λmax。根据概率理论,在λmin~λ区间微凸体的累积概率为 式 中:当λ→λmin时,R=0;当λ→λmax时,R ≈1。因为最大微凸体与最小微凸体直径相差很大,所以式(4)中R 的取值在0~1。 式(4)可变形为 因为微凸体在多孔介质壁面上是随机分布的,且大小服从分形标度,所以式中的R 是一组0~1 的随机数,通过随机抽样,可以得到微凸体直径分布的概率模型。 当微凸体直径从小到大排序后,可根据式(7)求得微凸体的个数。 单个微凸体的名义面积可表示为π(Lc/2)2,其中Lc为微凸体表面的名义特征长度,因此可得总的微凸体名义面积Aa φ由式(9)决定[18]。 式中:φ——有效孔隙率;r ——孔隙直径,这里把孔隙表面上的微凸体分布类比于分形多孔介质的孔隙分布;dE——欧几里得维数,二维空间内为2,三维空间取3。由于实际计算情况的需要,孔隙率φ常直接在0~1 之间进行取值。 根据多孔介质中的孔隙直径和孔隙数目满足的标度关系[19]可知,接触点直径分布也遵循同样的标度关系,具体如式(10): 可以看出,接触点直径的概率的密度函数n(λ)可由式(11)求得 可知,所有接触点面积之和Ar近似为 此处Ar为所有接触点的面积,即流体流过粗糙面时流体与粗糙面能够接触到的面积,本文也是用它来形容粗糙表面的粗糙程度的。当流体流经相同截面的光滑表面和粗糙表面时,与流体的接触面积粗糙表面要比光滑表面大;反之,当截面一定时,与流体的接触面积越大的表面也就越粗糙。 多孔介质粗糙表面的传热,可近似看作多孔介质某一截面上的过程传热,热流仍需经过孔相和固相,只不过此时的固相与经过截面时的固相不太一样。考虑截面传热时,热流经过的固相就是固体骨架的截面;考虑粗糙表面时,流体除经过孔隙外,还要考虑流体与固相接触的面积,而非全部固相的截面积。流体与粗糙固相接触面积由式(12)表达。 对于孔隙的面积,可由微元法得到,多孔介质横截面上孔隙总面积为 由傅里叶定律知传热系数k 如式(14): A 为多孔介质传热截面积,Ls为表面的名义特征长度,表达式为 热量Q 为多孔介质粗糙面吸收的热量。 式中:Q1——多孔介质孔隙吸收热空气的热量;Q2——多孔介质粗糙固体面吸收的热量。 式中:Ax——孔道的平均截面积;ca——空气的比热容;ρa——空气密度;v ——热空气流动的速度;t——加热时间;ΔT——加热前后的温差。 式中:cl——固体的比热容;ρl——固体的密度。 总热量Q 为 因为多孔介质结构复杂,所以热量通过多孔介质的不同相时,导热路径不同,得出改进后的傅里叶导热定律[17]。 联立式(12)—式(15)、式(19)、式(20)可得传热系数k 如下: 通过对联立后的传热系数计算,以及对变量的调整对比,可得分析图如图4 所示。 图4 有效传热系数模拟值与实验值比较Fig.4 Comparison of simulated and experimental values of effective heat transfer coefficient 图4 是以氧化铝为实验对象,其传热系数随孔隙率变化的实验数据[20]与模拟值的对比图。从图中可以看出,有效传热系数随孔隙率的增大而减小。实验数据较模拟数据稍稍偏小,考虑到实验存在一定的误差,所以该偏差是在实验误差允许范围内的,该模拟值能够很好地反映出多孔介质粗糙表面传热系数随孔隙率变化的关系,可用于计算多孔材料粗糙表面的等效导热系数。本文是基于粗糙表面的分形蒙特卡罗法进行的推导验算,并且与实验数值有很好的验证,所以可用于多种多孔介质粗糙表面的传热分析,如:粗糙墙体保温、地下石油开采、机械零部件的传热等。 图5 是面积分形维数对粗糙面的影响,这里的粗糙面的粗糙程度并不是通过粗糙度体现出来的,而是由流体与粗糙面的接触面积的大小而体现的,当接触面积越大时,粗糙面就相对越粗糙,当接触面积越小时粗糙面就相对没有那么粗糙。通过图5 可以看出,所有接触点的面积随面积分形维数的增大而增加,也就是说面积分形维数越大时,相对接触面越大粗糙表面结构也就越复杂。通过图5 还能看出,所有接触面积的增长速度刚开始增长较慢,随面积分形维数的增大而增加得越来越快。 图5 面积分形维数对粗糙表面的影响Fig.5 Influence of surface integral shape dimension on rough surface 图6 是面积分形维数对有效传热系数的影响变化关系图。从图6 可以看出,当孔隙率一定时,有效传热系数随面积分形维数的增大而减小,减小趋势越来越大。因为当面积分形维数较小时,对有效传热系数影响较小,孔隙率对传热占主导因素;当面积分形维数较大时,其影响程度相对于孔隙率的影响程度较大。 图6 面积分形维数对有效传热系数的影响Fig.6 Influence of surface integral shape dimension on effective heat transfer coefficient 在面积分形维数较大时,不同孔隙率下,有效导热最后趋近于同一值;当分形维数一定时,有效传热系数随孔隙率的增加而减小。因为孔隙越大,其中的气相占比越大,气相的传热系数比固相的传热系数小,所以孔隙越大,有效传热系数越小。 (1)根据分形原理,考虑粗糙表面传热特殊性,结合蒙特卡罗法,建立粗糙表面的模型,并推导出关于粗糙表面的传热系数的表达式。该模型既考虑了传统的多孔介质的传热方式,又结合了蒙特卡罗法,能够更详细地顾及到细微结构对传热系数的影响。 (2)通过与实验数据对比发现,当面积分形维数一定时,有效传热系数随孔隙率的增大而减小,在孔隙率较小时减小的速率较快,在孔隙率较大时,减小的速率较小并逐渐趋于平稳,因为当孔隙率较大时,空气与粗糙表面接触的面积相对减小,而空气的传热系数较小,所以变化也就较小并趋于平稳。 (3)通过对多孔介质粗糙表面的蒙特卡罗-分形传热研究发现,面积分形维数越大时,粗糙表面越不平整,传热过程也就越复杂,所以会导致传热系数减小,同理,当面积分形维数较小时,表面区域比较平整,传热路径较短,耗时也就较少,传热系数较大。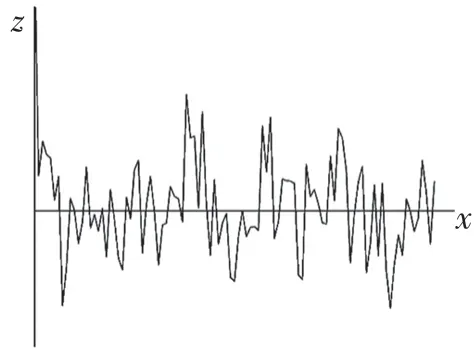
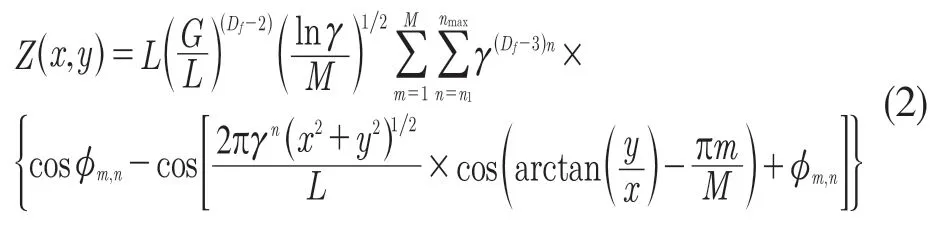
2 考虑多孔介质接触粗糙表面分形—蒙特卡罗方法
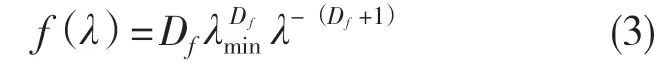
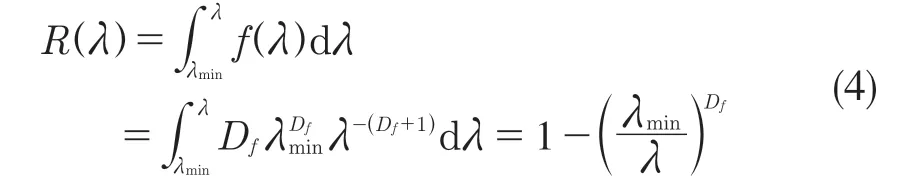
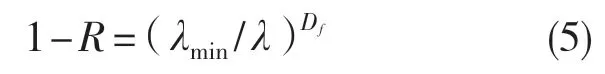
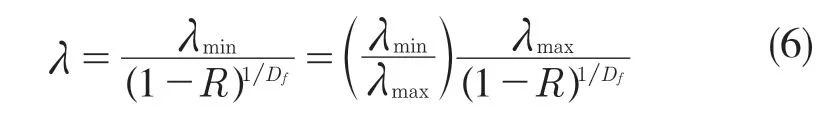
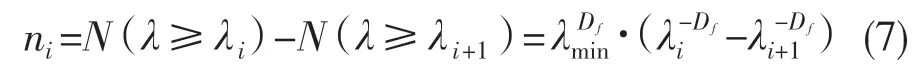
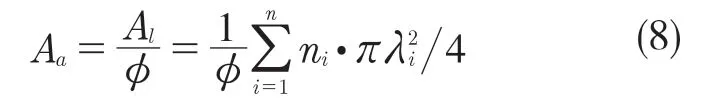
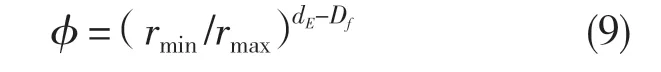
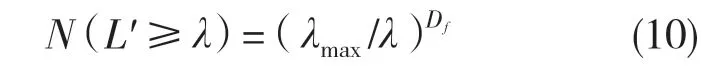
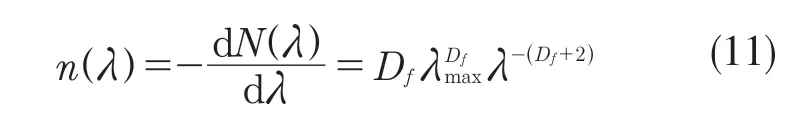
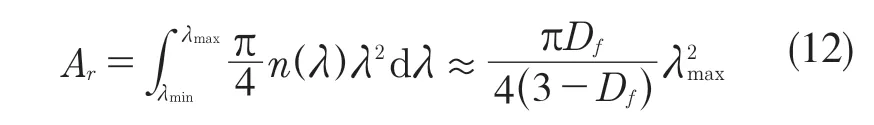
3 多孔介质粗糙表面传热系数的求解
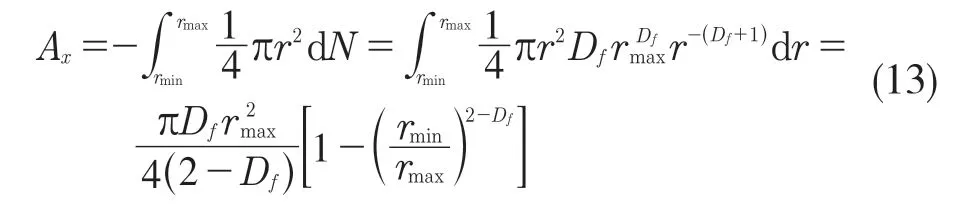

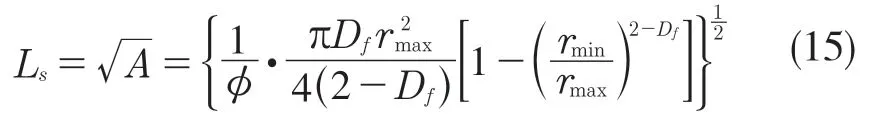

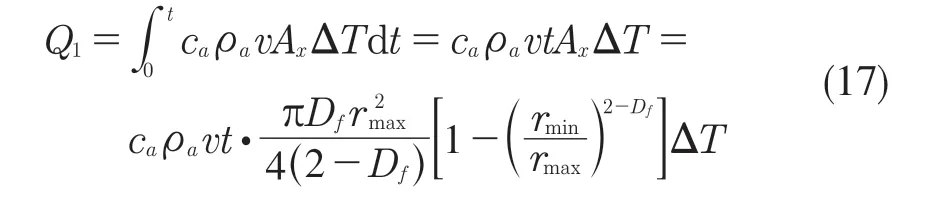
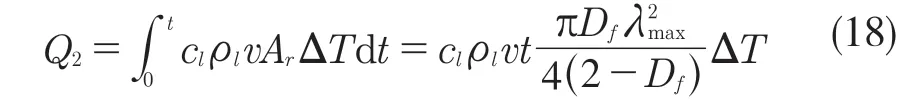
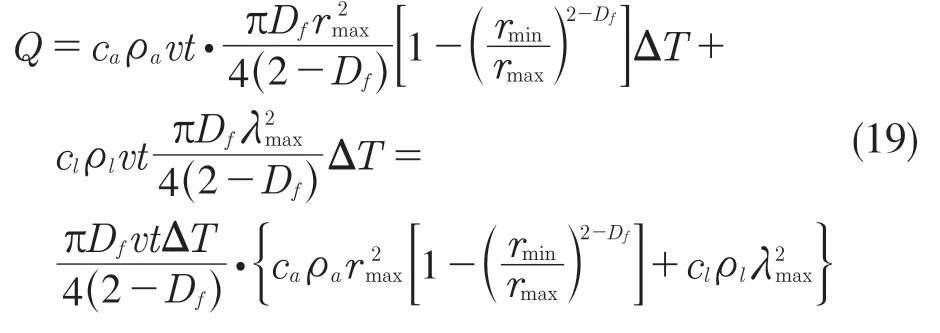
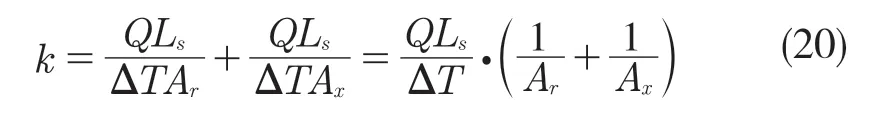
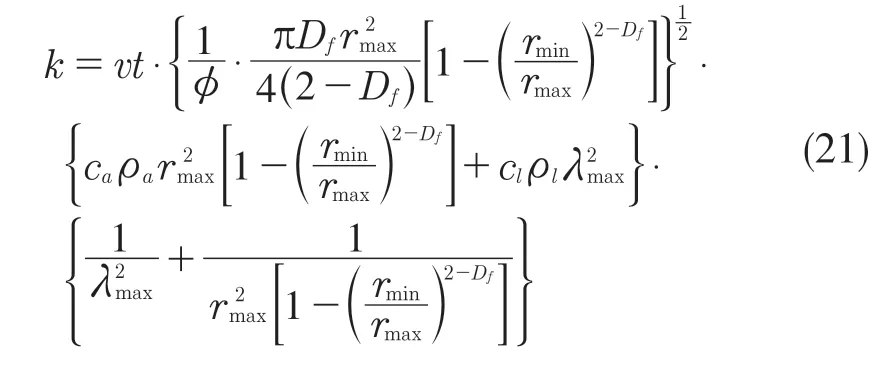
4 结果分析与讨论
5 结论

