基于二次响应面模型前保险杠低速碰撞优化设计

孙江，常高爽

（200093 上海市 上海理工大学 机械工程学院）

0 引言

现如今我国汽车保有量有了大幅度增加，汽车设计制造水平要求也不断提高，汽车造成的交通事故也越来越多。根据公安交通管理局的交通事故数据统计显示，交通事故一般分为4 种类型：前部碰撞、侧面碰撞、追尾碰撞和翻滚。前部碰撞中的低速碰撞是所有碰撞中所占比例最大的[1]。汽车碰撞时应尽可能多地吸收能量[2]，当车辆发生碰撞时，保险杠变形吸收能量，但是变形过大会影响到散热器、发动机等重要部件，合适的侵入量变形对刚度有要求，在结构、材料不变的条件下，通常增加厚度来增加其刚度，但同时质量也会增加，违背了轻量化设计，导致动力性和燃油经济性都变差。

相关研究中，Neraj Natarajan[3]等人对某汽车保险杠进行中冲和角冲低速碰撞分析，通过增加缓冲梁的厚度提高碰撞过程中的能量吸收；刘昭[4]等人通过使用改进的粒子群算法对汽车符合保险钢系统进行轻量化设计，优化后的保险杠系统不仅满足强度和耐撞性的要求，同时减重31.5%；袁敏[5]等人通过ANSYS Workbench 有限元仿真软件分析前纵梁的吸能特性，分析得出前纵梁横截面积越复杂其抗变形能力越大；穆伟[6]通过对铝制保险杠进行碰撞分析，获得不同优选指标的仿真结果，得到铝制保险杠的最优厚度；张友国[7]等人利用仿生结构改变两座电动车铝合金前防撞梁的截面形状，得出具有两个胚胎球形截面的防撞横梁耐撞性最优；李超超[8]等人提出利用铝合金吸能和结构有限元模型优化其吸能特性的方法，得出适当增加吸能盒壁厚可以提高吸能特性，以及吸能盒截面形状和有无V 型诱导槽对吸能特性影响更为突出。

以上研究中，有的分别从汽车横梁和吸能盒单个方面对汽车前保险杠耐撞性进行评价与优化，或者是将横梁和吸能盒作为一个整体进行研究，但是优化方法过于粗糙，因此本文以某款乘用车的前横梁和吸能盒作为一个整体，通过低速仿真分析，基于二次响应面近似模型进行优化，保证其在有一定的耐撞性的前提下，对其进行轻量化处理。

1 前保险杠低速碰撞仿真

在前保险杠有限元建模中，横梁和吸能盒都为壳单元。该模型一共有9 个部件，26 017 个单元，21 167 个节点。图1 所示为其有限元模型。

图1 前保险杠有限元模型Fig.1 Front bumper finite element model

汽车的前后保险杠系统有一定挠性，在发生碰撞时，能保护乘员的生命安全。所以在对汽车进行轻量化设计时，不能无限制地追求质量减小，还要考虑到车辆耐撞性能。汽车前防撞梁的碰撞性能评价指标主要包括：碰撞器侵入量、横梁和吸能盒总质量，应该通过控制侵入量来保证轻量化方案的可行性。

本文选取保险杠前横梁和吸能盒初始厚度分别为2.4，1.8 mm,保险杠的总质量为16.21 kg，通过LS-dyna 进行碰撞仿真分析。根据GB 17354-1998《汽车前、后端保护装置》规定，设置碰撞时间为0.12 s，碰撞速度为4 km/h。图2 所示为保险杠各阶段位移云图。

由图2 可以看出，汽车前保险杠的横梁和吸能盒产生了不同形状的变形。图3 为保险杠碰撞过程中的能量变化曲线。从能量-时间曲线可以看出，碰撞的动能几乎全部转换为保险杠的内能，在0.05 s 之后是因为保险杠的弹性恢复，导致系统内能开始减小，动能开始增加，之后系统能量转化趋于稳定。从图3 可以看出，沙漏能远远低于总能量的5%，说明此有限元模型是可靠的，可以进行接下来的仿真分析和优化设计。

图2 碰撞过程中保险杠碰撞云图Fig.2 Bumper collision cloud map during collision

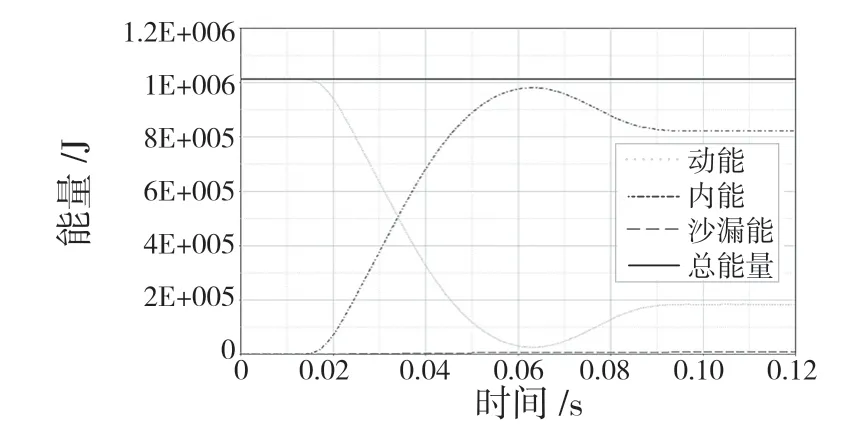
图3 碰撞过程中能量变化曲线Fig.3 Energy change curve during collision

如图4 为保险杠后端侵入位移。可以看出，保险杠后端侵入位移最大值为46.233 mm。为保证前车箱内发动机等关键部件在碰撞时损坏程度最低，以及保证车内乘客的安全，要求将入侵位移尽可能控制在不损害其他关键部件。

图4 保险杠后端侵入位移Fig.4 Intrusion displacement of rear bumper

2 优化目标代理模型的建立

2.1 优化设计基本参数

汽车的设计越来越追求良好的动力性和燃油经济性，所以对于轻量化的要求越来越高。汽车轻量化的设计也要兼顾到汽车的刚度等安全性问题。当车辆发生低速正面碰撞时，前保险杠的过多侵入会损坏到车身其他部件，影响到车辆碰撞的耐撞性。因此有必要将侵入量、横梁和吸能盒的总质量为优化目标。在进行目标优化时，避免侵入量过大，可以将侵入量作为一个约束条件。

为使汽车前保险杠有更好的耐撞性能的同时兼具轻量化，本文将横梁厚度和吸能盒厚度作为设计变量，横梁的初始厚度为2.4 mm，吸能盒的初始厚度为1.8 mm，在初始值厚度的基础上增减30%,作为横梁及吸能盒的上下限。厚度变化如表1 所示。

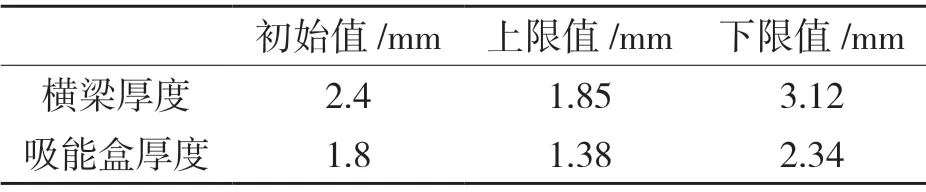
表1 优化设计变量值Tab.1 Optimize design variable value

2.2 试验设计和建模

2.2.1 最优拉丁超立方试验设计

最优拉丁超立方试验设计（Optimal Latin hypercube Design,Opt LHD）是一种在拉丁超立方试验设计（Latin hypercube Design,LHD）基础上改进的随机抽样法，它可以保证整个变量空间都被样本点覆盖。最优拉丁超立方试验的样本点是随机抽样进行组合的，每一次都能得到不同的结果，这样就可以研究出不同的组合结果，使其拟合结果更加准确可靠，因此本文选用最优拉丁超立方试验设计。

为使汽车前保险杠有更好的耐撞性能的同时兼具轻量化，对保险杠横梁和吸能和盒的厚度进行优化。在初始值上下30%左右的范围内通过优化的拉丁超立方选取10 个样本点代入仿真分析得到入侵量和总质量的仿真值。如表2 所示。

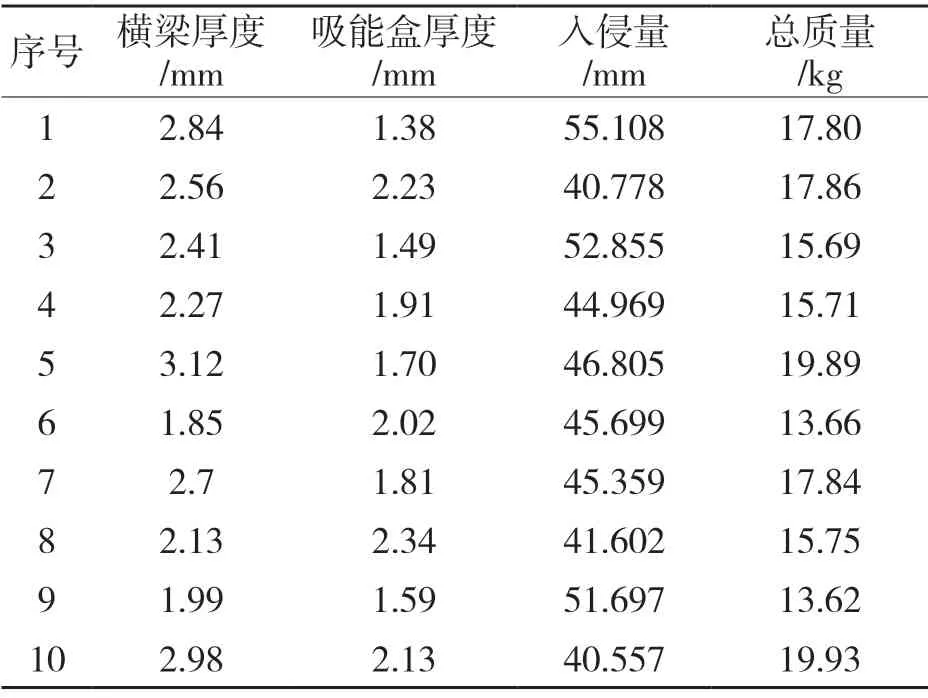
表2 检验样本点及优化目标仿真值Tab.2 Test sample points and optimization target simulation value

2.2.2 建立近似模型及验证

多项式响应面（Polynomial Response Surface,PRS）在结构优化领域得到广泛的应用。利用回归分析决定设计变量和响应间的关系。在多项式响应面模型中常用的主要有可以提供设计变量和响应之间的显式关系的一次和二次多项式响应面模型。本文将采用二次多项式响应面模型（quadratic polynomial response surface，QPRS）对上述的设计变量与响应建立近似模型，其数学表达式如下：

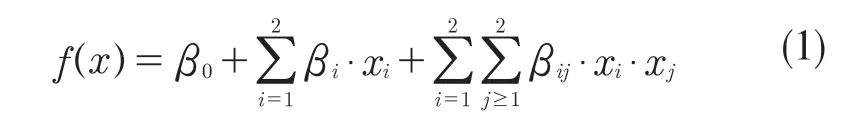
式中：xi——二维自变量x 的第i 个分量；β0，βi，βij——未知参数，构成列向量β。

优化拉丁超立方抽样结果，以横梁和吸能盒的厚度为设计变量，以侵入量、横梁及吸能盒总质量为响应，建立二次多项式响应面模型。

为了计算结果的准确性，需要对近似模型进行验证，模型精度越高，基于近似模型的多学科优化最优解的可信度也越高。决定系数（R2）表示自变量或误差对因变量的相关性，R2越接近1，数学模型和原模型之间的误差越小，拟合精度就越高。模拟拟合精度可通过决定系数来判断，其数学表达式如下：

式中：n——样本点数量；yi——真实响应值；——响应面模型计算所得的响应值；——真实响应值的平均值。

二次多项式响应面近似模型侵入量和总质量两个响应量的预测值与实际值的分布如图5 所示。入侵量响应量和总质量响应量的决定系数（R2）为0.960 1 和0.999 8，模型精度非常高，符合要求，可应用于下一步的优化算法。

图5 QPRS 近似模型侵入量（a）、总质量（b）样本点分布Fig.5 QPRS approximate model invasion amount (a),total mass (b) sample point distribution

3 前保险杠多目标优化

3.1 建立优化模型

本文以保险杠横梁x1和吸能盒厚度x2为设计变量，以保险杠后端入侵量L(x)和总质量M(x)为目标函数，考虑到横梁的入侵量过大会造成车身的损伤从而影响车辆碰撞的耐撞性，本文以入侵量L(x)为约束，以略小于初始入侵量56 mm 为上限，建立多目标数学优化模型如下：

3.2 优化结果

非支配排序遗传算法NSGA-II（Non dominated sorting genetic algorithm-II）是目前最流行的多目标遗传算法，它提出了快速非支配排序算法，一方面降低了计算的复杂程度，另一方面保留了最为优秀的所有个体，具有运行速度快、解集的收敛性好的优点。

本文采用NSGA-II 进行优化，算法参数如表3 所示。

表3 NSGA-II 算法参数Tab.3 NSGA-II algorithm parameters

经过1 000 次迭代得到最优解方案为x1=1.85，x2=2.339。近似模型算得预测响应值侵入量L（x）=41.267 mm，总质量M（x）=14.25 kg。为了更贴近实际工艺制造要求，将横梁厚度值与吸能盒厚度值最优方案取小数点后1 位，将方案x1=1.9，x2=2.3代入LS-DYNA进行有限元仿真求解,计算得侵入量为43.033 mm，总质量为14.44 kg。优化点的预测值与仿真值对比如表4 所示。

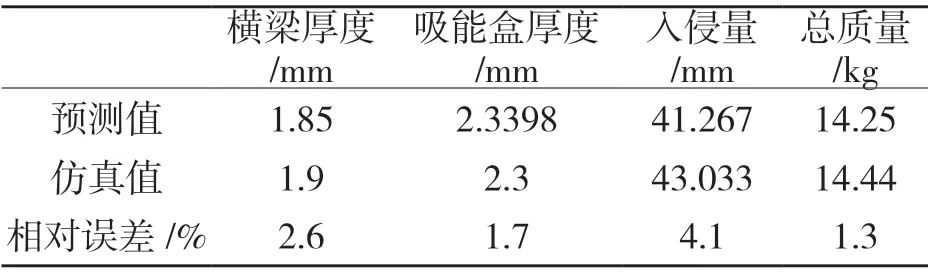
表4 优化点的预测值与仿真值对比Tab.4 Comparison of predicted and simulated values of optimized points

由表4 可知，入侵量的仿真值与预测值之间的相对误差为4.1%,总质量的仿真值与预测值之间的相对误差为1.3%，都在可以接受的范围内。

在车辆低速行驶时，碰撞力峰值过大会影响到前保险杠后面其他重要的部件，从而降低车辆的耐撞性。如图6 优化前后碰撞力随时间变化曲线所示，优化前的碰撞力峰值为3 234，优化后的碰撞力峰值为2 128。

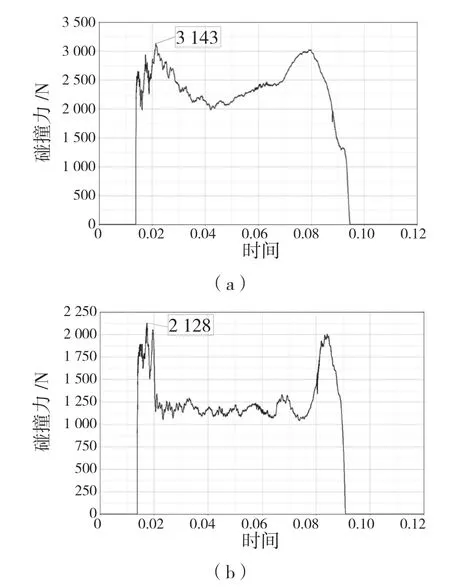
图6 优化前（a）和优化后（b）碰撞力随时间变化曲线Fig.6 Time curve of collision force before optimization (a) and after optimization (b)

前保险杠横梁及吸能盒优化前后有关参数对比如表5 所示。

如表5 所示，与优化前相比，入侵量为43.033 mm，比优化前降低了3.2 mm。优化后碰撞力峰值为2 128 N，比优化前降低了1 015 N，前保险杠的耐撞性明显提高。优化后横梁及吸能盒总质量为14.44 kg，减少了1.77 kg，前保险杆的质量显著降低。从汽车碰撞安全性与汽车轻量化的角度考虑，可以认为最终的仿真结果达到了优化设计的目的。

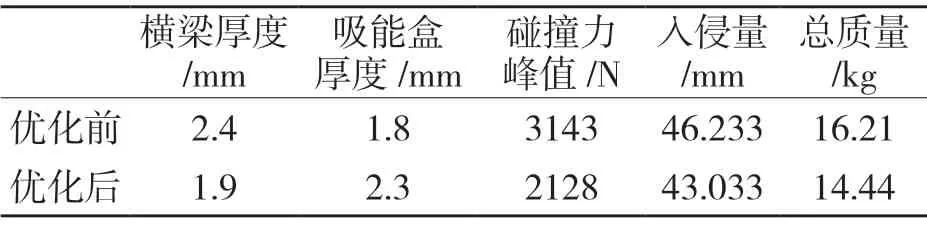
表5 优化前后有关参数对比Tab.5 Comparison of relevant parameters before and after optimization

4 结论

本文通过优化超拉丁试验，建立近似模型。以横梁及吸能盒厚度为设计变量，经过非支配排序遗传算法得到最优横梁厚度1.9 mm，吸能盒厚度2.3 mm。结果显示总质量降低了1.77 kg，入侵量和碰撞力峰值分别也降低3.2 mm 和1 015 N。本文在对前保险杠优化设计中不仅满足了轻量化的要求，同时还提高了耐撞性。