基于Fluent 的离心式吹吸机的结构分析与优化

李纪行

（200093 上海市 上海理工大学 机械工程学院）

0 引言

随着时代的进步和我国工业化、城市化的发展，环境问题得到了人们的广泛关注。城市园林绿化建设带动了园林器械的发展。吹吸机是园林机械的一种，市场需求十分旺盛[1]。离心式吹吸机作为离心式风机的一种，研究分析好离心式吹吸机对以后研究相关的离心式风机有很大帮助。

离心风机主要由叶轮、进风口及蜗壳组成。当叶轮跟随电机提供的转动轴转动时，空气由于受到离心力的作用而被甩出。甩出的气体被挤到机壳中使得机壳内部气压增强，最终从导向口排出。气体被排出后，叶轮中心部分的压强降低，外界气体就能从风机的吸入口通过叶轮前盘中央的孔口吸入，源源不断地输送气体[2]。

风机的研究有很多种方法，最主要的就是实验研究、理论研究和数值模拟这三种方法[3]。由于数值模拟研究具有成本低、降低优化难度等特点，被人们广泛应用。随着计算机技术的出现，以及应用计算机技术解决物理问题精确值算法的发展，计算流体动力学成为计算流体力学的一种很重要的方式。本文中通过CFD 对此吹吸机中的关键零部件进行分析，对其进行优化，提高风机的效率，从而减少样机制造和实验所需的资源及时间成本。

1 建立离心式风机有限元模型

因为模型的建立必须遵循物理的真实性和数学的可行性这两个原则，所以本文讨论如图1（a）所示的Homelite 的TTI7A 系列的离心式吹吸机，为了满足后续网格划分和流场特性计算，简化模型如图1（b）所示。

图1 动力学模型的建立Fig.1 Establishment of the dynamic model

将SolidWorks 建立的风机简化模型另存为Iges 格式，再用HyperMesh 软件进行数值模拟的前处理——网格划分[4]，离心式风机各部件采用的是四面体网格划分，网格划分主要细节如表1所示，划分的网格如图2 所示，效果示意图如图3 所示。

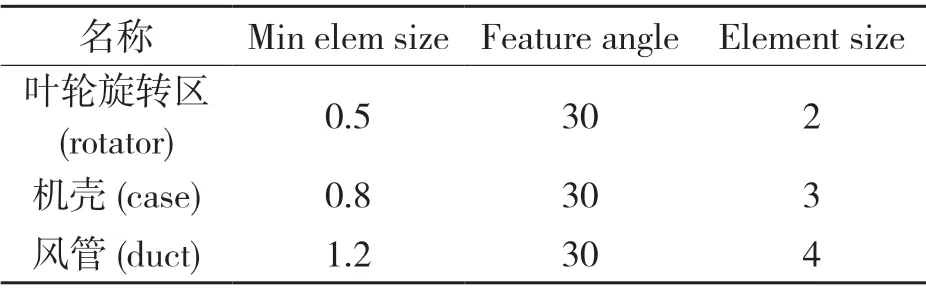
表1 离心式风机各部件的网格划分尺寸Tab.1 Mesh size of each component of a centrifugal fan

图2 体网格生成示意图Fig.2 Schematic diagram of grid generation in body

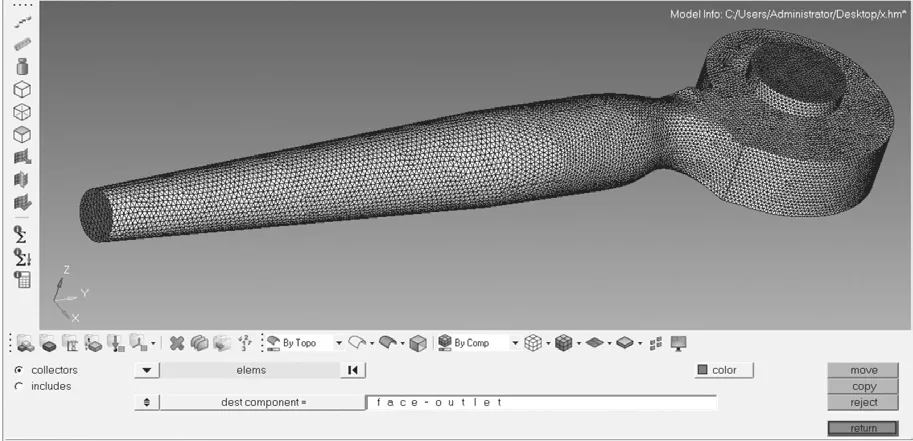
图3 离心式风机网格划分效果示意图Fig.3 Schematic diagram of grid division effect of centrifugal fan

2 有限元仿真结果分析

2.1 基于Fluent 计算求解

选择Standard k-ε的湍流模型[5]，定义风机材料为气体，水力直径分别是进风口1 为70 mm、进风口2 为56 mm、出风口为38 mm，仿真模型的旋转速度设置为15 000 r/min。将模型初始化后，进行迭代运算。

图4（a）是原风机的速度矢量云图，图4（b）是原风机的压力云图。从速度矢量图上可以显示出，在风机旋转区域内叶轮上叶片周围的速度最大，也就是流体经过叶轮后由于离心力被甩出的过程中速度逐渐在增大，从叶轮排出后，速度在降低。从图4（a）中可以看到，靠近蜗壳出口的地方速度比其他叶轮通道内的速度小得多，而蜗舌处有速度微小的回流现象。静压力分布图中，叶轮的进出口的地方显示最低的静压力，蜗壳内部的静压力由叶轮中心向外逐渐增大，由于流动损失，沿着风管出口处的静压力逐渐降低。

图4 Z=0 的速度矢量图与压力分布图Fig.4 Velocity vector diagram and pressure distribution diagram of Z=0

图5 是叶片工作面。从图5 可以看出，叶片工作面上的静压力分布不均匀，工作面上对空气做功的程度最大，非工作表面上静压力分布较均匀，压力分布是从叶片根部逐渐增大，符合文献[6]中叶轮内部的流动特性。

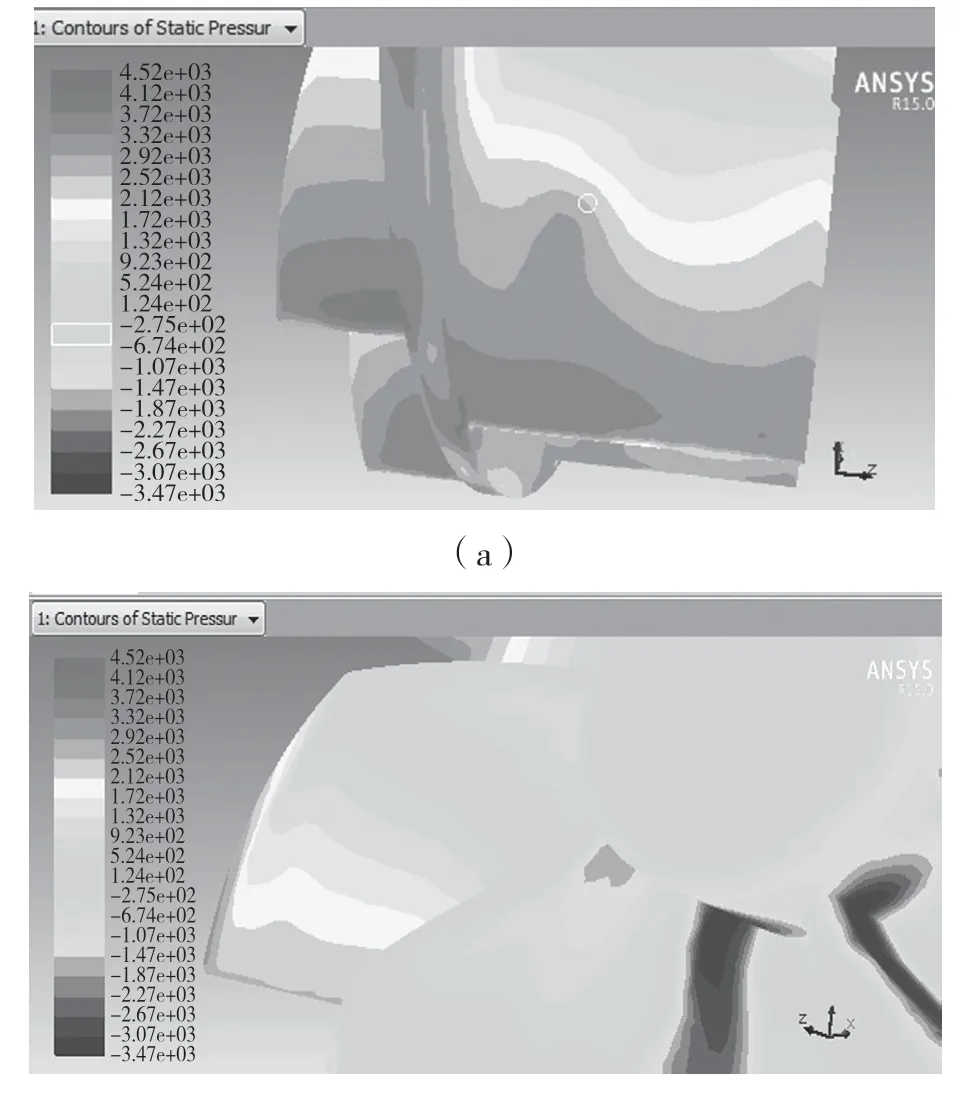
图5 叶片的工作面应力分布图Fig.5 Working face stress distribution diagram of blade

经数值模拟分析，风机重要性能参数是：出口流量为0.111 1 kg/s，全压是4 033.44 Pa，力矩是0.426 N·m，根据公式P轴=（其中：n——转速；T——转矩）可以求出轴功率为668.82 W，由效率公式η=×100%计算得出此风机的效率是53.6%。

2.2 优化方案数值模拟分析

2.2.1 蜗舌半径对风机性能的影响

在风机结构中，蜗壳对其性能也有很大的影响，尤其是叶轮出口处，它的气流与蜗舌之间会产生剧烈的撞击，所以蜗舌的附近会产生强烈的旋涡，使得蜗舌边缘流动比较复杂。由于强烈的旋涡会产生气体的回流，所以第一个方案采用更改蜗舌的半径以达到提高风机的效率。

经过测量，原模型蜗舌部位的半径为5.22 mm，所以在设计方案时，为了简化方案，将蜗舌半径分别改为2，3，4，6，7，8，13 mm，经上述网格划分与流场分析计算可得表2 所示数据。

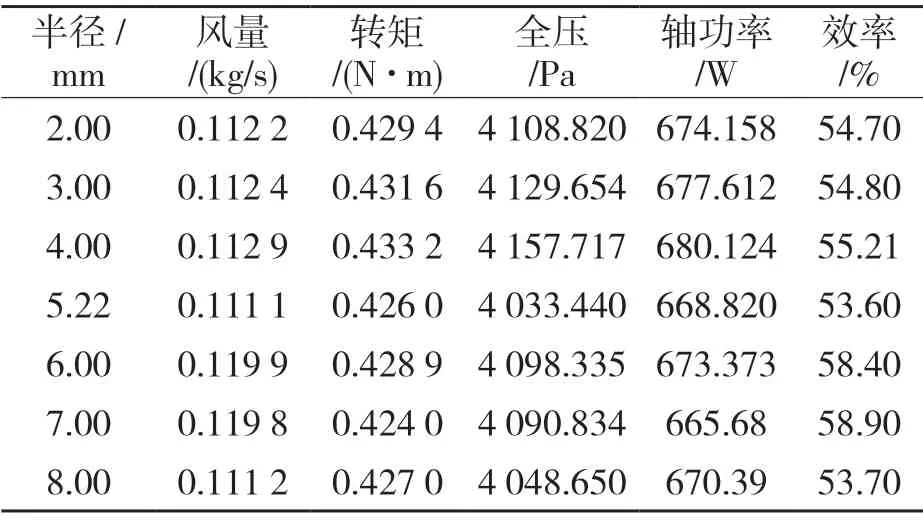
表2 蜗舌半径变化数据处理结果Tab.2 Data processing results of volute tongue radius variation

半径小于原值时，进行比较可以发现，半径是2，3，4 mm 处的效率都比原来风机的效率高，尤其是半径为4 mm 时，效率提高了1.6%，但它的轴功率也是在数据里面最高的，所以在比较的过程中可以发现，半径为7 mm 的效率最高，而且所需的轴功率最低。

2.2.2 叶片弧度对风机性能的影响

离心式风机的叶片基本上有3 种：直线型、圆弧型、机翼型。研发人员会在设计过程中发现机翼型叶片风机的效率是最高的，而且噪音又低。而通过传统的设计理念和手工建模的方式，很容易产生误差很大型面，风机的流体动力学特性很难保证。翼型原理[7]如图6 所示。其中，b 为翼型中心线两端点的距离，为翼弦；a 指最大弯度的相对位置；θ指翼型的弯折角。

图6 机翼叶片计算原理Fig.6 Calculation principle of wing blade

翼型中线由一段圆弧构成，中线在xoy 面上的坐标方程为

抛物线构成的翼型中线方程为

翼型的上轮廓

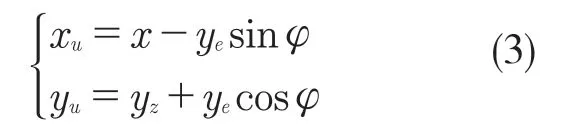
翼型的下轮廓

选取翼型截面为NACA4409 数据，采用表格计算功能，将上下弦的公式输入表格内进行坐标计算，再带入SolidWorks 三维软件中画出叶片三维图。由于原风机的叶片在80°左右，所以采用翼型数据时，选取参数转折角θ为60°～90°。

从表3 中可以看出，选用翼型叶片时，转折角的增大不仅使得风量提高，效率也同时提高很多。从表3 可以得出在90°时效率最高。

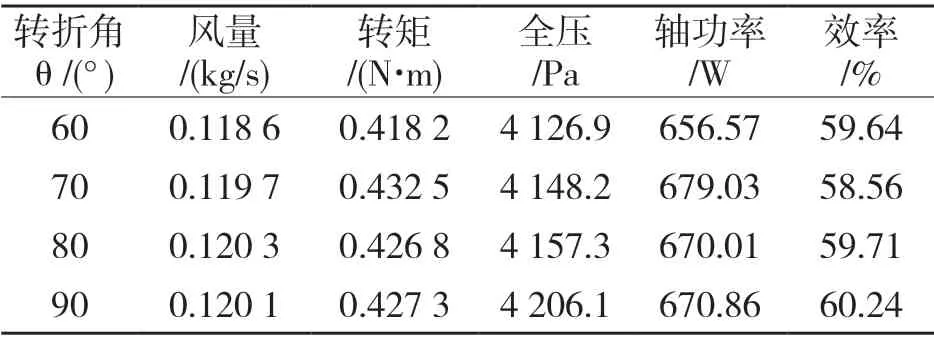
表3 叶片转折角变化数值结果分析Tab.3 Analysis of numerical results of blade turning angle variation

2.2.3 叶片数目对风机性能的影响

风扇叶片数的不同对轴流风机的气动效果有很大的影响，叶片数过少时，风扇风量会变低，而叶片数过多时，又会使得空气流动空间减小，因此一个合适叶片数的选择是很重要的。本文在原有叶片的基础上改动叶片的数目，选取数量在6～12 之间。

通过表4 可以清晰地观察到，随着叶片的数目的增加，风量也在逐渐增大，但是所需的轴功率也随之增大，与原风机的数据相比，选择叶片数目为10，轴功率增加的幅度不是很大，而且效率提高了0.6%。

表4 叶片数目改动数值结果分析Tab.4 Numerical results analysis of blade number changes

3 结论

本文主要从各个部位结构参数的变化分析离心式风机的流场特性，以出口的流量、风机轴功率以及全压效率的大小为评价点对风机的蜗舌半径、叶片形状、原叶片数3 个参数进行数值模拟，观察每个参数变化后的最优值。

综上所述，最后的优化结果是将原有蜗壳上蜗舌的半径改为7 mm，采用弧度为90°的翼型叶片，叶片数目为10。