细长薄壁件旋锻成形工艺研究
王宏,卢曦
(200093 上海市 上海理工大学 机械工程学院)
0 引言
细长薄壁件是壁厚较小、长径比大于25 的零件统称,因其壁厚较小,通常具有节约材料、减少产品质量等优势,广泛应用于造船、航空航天、核能、军工等高尖端行业[1]。细长薄壁类零件因其长度方向尺寸较长,刚度较差等原因,普通加工成形质量相对较差,因此应针对产品结构特点和相关要求,对其成形工艺进行研究。
细长轴类薄壁零件的成形方法种类繁多,针对不同零件结构特点和要求,应选取不同的成形方法。张开学[2]等针对薄壁细长轴在车削成形过程中的问题,通过调整加工工艺、改变装夹方法等提高细长轴的加工精度和加工效率;刘峰[3]等针对材料流动性差、易产生气孔等缺陷,通过改进工艺参数,有效提高成形质量,符合各项质量要求;尹冠人[4]等分析薄壁管在旋锻成形中的受力特点,研究了成形过程中摩擦条件对产品成形尺寸的影响;王聚存等针对细长轴难加工问题,提出采用旋锻成形工艺方案。通过试验验证,采用该工艺能有效保证产品成形质量[5]。本文重点研究细长薄壁件成形工艺,根据产品结构特征与产品要求确定成形工艺方法,通过有限元分析确定该成形工艺下的进给参数,根据进给参数数值模拟确定该工艺路线下产品成形的应变、金属流动及损伤分布,分析该成形工艺方案的可行性和进给参数的合理性,为产品实际加工成形提供参考。
1 材料与方法
本文以细长薄壁件为研究对象,产品的尺寸如图1 所示。

图1 产品尺寸图Fig.1 Product dimension drawing
该产品总体积为11 080 mm3,总长度为266.7 mm,外径等长为9.5 mm,内径从左到右依次增大,最小内径为4.3 mm,最大内径为4.5 mm,长宽比接近28.1,是一种典型的细长薄壁类零件产品。该细长薄壁件的材料为GH3625,其材料成分如表1 所示。

表1 材料成分Tab.1 Material composition
对于细长薄壁件成形工艺研究,本文提出的研究方法如下:
(1)首先根据产品的尺寸结构特点和相关要求,提出合理的成形工艺方案。
(2)其次通过尺寸关系和数值模拟,确定合理的进给参数。
(3)最后根据进给参数,通过数值模拟分析该工艺参数下的应变、速度场以及损伤分布。
2 成形工艺分析
在工程应用中,对于细长薄壁类零件一般可通过车削、铸造、旋锻等多种类型方式完成。车削是通过刀具对旋锻的工件进行车削加工,主要适用于对称旋转体的加工成形;铸造是将液体金属浇铸到与零件形状相适应的铸造空腔中,待其冷却凝固后,以获得零件或毛坯的方法;旋锻成形属于回转塑性成形工艺类,是利用材料的塑性,通过机器作用于模具对坯料施加径向作用力,迫使材料发生变形,依据模具和芯棒尺寸得到理想尺寸产品的特种成形工艺方法。旋锻成形不仅能加工各类不同形状及尺寸的产品,而且加工精度高,能够改善材料组织,提高其力学性能,是现代细长轴成形的重要方法。参见图2。

图2 旋锻成形图Fig.2 Forming drawing of rotary forging
由于该细长薄壁件内壁壁厚连续变化,普通的车削难以精确加工产品内径。同时,毛坯内径较小,车削过程中易出现排屑困难;另一方面,坯料过长,毛坯在刀具切削力的作用下产生变形,破坏毛坯与刀具之间的相对位置,导致加工存在严重误差。若采用铸造工艺,该材料为高温合金材料,金属流动性相对较差。同时,产品为细长薄壁件,铸造工艺难以成形,而且液体金属在冷却凝固过程中,内外壁容易产生细微气泡与沙眼,影响产品质量。根据产品尺寸相对较小,强度与精度要求相对较高,应初步选择旋锻成形工艺,以保证成形质量和成形精度,具有一定的优势。
3 进给参数确定
通过上述分析,初步选择旋锻成形工艺,主要成形参数为径向进给量、周向进给量以及轴向进给量。
3.1 径向进给量确定
径向进给量即设备通过模具对坯料的下压量。在含芯棒成形工艺中,径向进给参数主要由毛坯外径尺寸和产品外径决定。含芯棒成形工艺中,径向进给量如式(1)所示:

式中:Δh——含芯棒旋锻成形径向下压量;D——毛坯初始外径;d——产品外径。
在含芯棒旋锻成形中,毛坯初始外径为10.5 mm,产品外径为9.5 mm,根据式(1)确定含芯棒成形工艺中径向进给量为0.5 mm。
3.2 周向进给量确定
周向进给量即在一次径向进给后,毛坯相对模具转动角度。周向进给量与毛坯外径变形位置相关,以锻打后的毛坯最小变形位置决定。在含芯棒成形过程中,毛坯在进给量为0.5 mm 的径向下压量下,毛坯内径与芯棒完全贴合,外径变形通过点刻画得到,如图3 所示。为便于观察外径变形情况,将外径放大一定倍数,如图4 所示。

图3 外圆尺寸图Fig.3 Cylindrical dimension drawing
如图4 所示,毛坯最大变形位置为毛坯与模具中心接触位置,即0°,90°,180°,270°;毛坯最小变形位置为模具间的间隙区域,即45°,135°,225°,315°。根据最小变形位置确定一次周向进给量为45°。

图4 外圆尺寸放大图Fig.4 Enlarged drawing of outer circle size
在第1 次周向进给45°后,外径尺寸发生明显变化,毛坯外径尺寸如图5 所示。为便于观察内外径变形情况,将外径放大一定倍数,如图6 所示。

图5 外圆尺寸图Fig.5 Cylindrical dimension drawing

图6 外圆尺寸放大图Fig.6 Enlarged drawing of outer circle size
如图6 所示,在一次周向进给后,毛坯最大变形位置在0°及其对称位置,毛坯最小变形位置在30°及其对称位置,根据最小变形位置确定二次周向进给量为30°。同理,确定后续周向进给量分别为25°,30°,20°,25°,35°。
通过多次周向进给,毛坯外径尺寸不断变化,采用最大内接圆法和最小外接圆法,即“圆度”概念定量表征成形表面质量,圆度定义如式(2)所示:
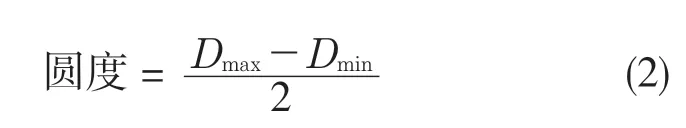
根据周向进给量不断变化,周向进给道次增加,外圆质量不断提高,外圆圆度随周向进给道次的关系如图7 所示。
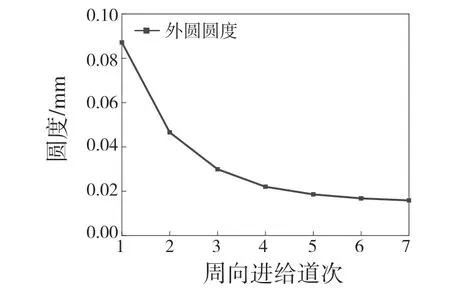
图7 外圆圆度与进给道次关系Fig.7 Relationship between roundness and feed pass
如图7 所示,随着周向进给道次不断增加,毛坯外圆圆度不断降低,在前期周向进给时,毛坯外圆圆度显著提高,在后期周向进给时,毛坯外圆圆度降低不明显。当周向进给道次为6 时,毛坯外圆圆度基本不变,因此确定周向进给最低道次为6。
根据旋锻成形自动化控制要求,应将周向进给量统一化处理。根据上述分析,周向进给量分别为45°,25°,30°,20°,25°。选取周向进给量的中位数25°作为统一化后的周向进给参数,得到统一化前后的外圆尺寸如图8 所示。

图8 外圆圆度与进给道次关系Fig.8 Relationship between roundness and feed pass
如图8 所示,周向进给量统一化前后的外圆尺寸相差较小,圆度基本不变,满足产品要求,因此可将周向进给量统一化为25°。
3.3 轴向进给量确定
轴向进给是含芯棒旋锻成形过程中毛坯和芯棒相对于模具的轴向进给量,是含芯棒旋锻成形的重要进给参数之一。若轴向进给量设置不合理,不仅缩短设备寿命,而且造成产品组织纤维断裂、产品表面出现裂纹等情况发生,甚至对产品造成损伤,影响产品成品率。若工件沿轴向进给量过大,前后两次模锻击打位置间会出现材料的凸起,从而降低表面质量。
轴向进给量主要受模具几何尺寸以及径向下压量的限制,还受应变等多方面限制。在含芯棒旋锻成形过程中,轴向极限进给量应低于模具斜面与毛坯接触面在水平方向上的投影距离,具体如图9 所示。
根据图9,可得轴向极限进给量:
式中:L——轴向极限进给量;D——毛坯初始外径;d——产品外径;α——模具入口角。
根据毛坯初始外径约为10.5 mm,产品外径为9.5 mm,模具入口角度α 为10°,确定含芯棒成形工艺中轴向极限进给量为2.83 mm。
根据轴向极限进给量,通过有限元分析确定不同轴向进给量与最大应变的关系,如图10 所示。

图10 轴向进给量与应变关系Fig.10 Relationship between axial feed and strain
如图10 所示,随着轴向进给量的增加,应变逐渐提高,但上升幅度较小。考虑到轴向进给较大将降低产品表面成形质量,轴向进给较小将影响产品成形效率,因此确定轴向进给量为2 mm。
4 仿真结果与分析
根据上述成形工艺分析和进给参数研究,通过有限元分析毛坯在成形过程中的应变分布、金属流动情况和损伤,从而确定进给参数合理性,判断成形工艺的可靠性。
4.1 应变分布
应变分布主要用于分析毛坯在模具作用下产生的变形,可根据应变分布确定进给参数的合理性。在成形过程中,毛坯应变分布如图11 所示。

图11 应变分布示意图Fig.11 Schematic diagram of strain distribution
如图11 所示,毛坯在成形过程中,应变分布均匀。与内表面相比,外表面应变相对较大,符合旋锻成形的实际情况[6]。其主要原因为毛坯外表面受到模具直接锻打成形,金属流动性高于内表面。
4.2 速度场分布
速度场分布主要分析毛坯在成形过程中的金属流动情况。在成形过程中,毛坯速度场分布如图12 所示。

图12 速度场分布示意图Fig.12 Velocity field distribution diagram
如图12 所示,毛坯在成形过程中出现明显的中性层,中性层位于产品端,符合金属成形要求[7]。毛坯在受到模具作用力时,中性层两端金属一端向坯料端流动,另一端为周向流动和轴向流动。其主要原因为受模具锥角的影响,毛坯金属向坯料端移动产生“拔长”效果和径向移动进行减小内径的作用。
4.3 损伤分布
在有限元分析软件中,根据后处理中的Damage 对成形过程中毛坯的断裂、损伤进行分析,确定毛坯在成形过程中的损伤程度,预测毛坯在成形过程中发生塑性变形时易出现断裂和破坏的位置,进而判断成形工艺选择的合理性和进给参数确定的可靠性。
有限元软件中,采用Cockcroft-Latham 韧性断裂失效准则确定毛坯损伤程度,该失效准则认为材料损伤和破坏与材料所受最大拉应力相关。即对于特定的材料,当毛坯在拉伸状态下,材料的应变能达到临界值时,材料发生断裂,具体如式(4):
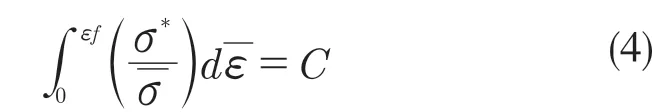
式中:——等效应力;σ*——最大拉伸应力;——等效应变增量;εf——断裂等效应变;C——损伤值。
通过有限元分析得到成形过程中毛坯的损伤分布如图13、图14 所示。

图13 横截面损伤示意图Fig.13 Schematic diagram of cross section damage

图14 纵截面损伤示意图Fig.14 Schematic diagram of longitudinal section damage
如图13 所示,毛坯内壁损伤高于外壁损伤,主要原因毛坯内部受到芯棒和模具双重作用,损伤最大值为0.19 左右。如图14 所示,毛坯外表面损伤均匀,损伤最大值为0.12 左右。根据上述分析,毛坯在成形过程中,损伤最大值均低于许可值0.45,符合要求[8]。因此,成形工艺中进给参数选择合理,毛坯在成形过程中不易导致产生损伤过大等问题。
5 结论
本文根据产品结构特点和要求,确定产品成形工艺。通过毛坯与产品尺寸关系及数值模拟确定进给参数。采用有限元分析该进给参数下的应变、速度场及损伤分布,得到结论如下:
(1)根据产品的结构特点和各成形工艺优缺点,确定采用旋锻成形工艺;
(2)根据毛坯外径与产品外径尺寸关系,确定径向压下量为0.5 mm;根据变形位置关系以及圆度要求确定周向进给量为25°;根据径向下压量、模具结构参数和应变要求确定轴向进给量为2 mm。其中,在周向进给过程中,前期周向进给道次对圆度降低效果较为明显。
通过有限元分析该进给参数下,毛坯在成形过程中应变分布、速度场分布、损伤分布均满足要求,确定该进给参数的合理性和成形工艺的可靠性,为其他细长薄壁件的成形工艺提供了参考。

