基于排土量与注浆量的盾构施工地表沉降预测

周奇才,沈鹤鸿,赵 炯,熊肖磊,王益飞

(同济大学 机械工程学院,上海 201804)

在盾构法施工过程中,不可避免地会引起施工隧道周围土体松动和沉陷,造成地层的损失,从而引起地表的沉降.当沉降超过一定范围时,将造成严重的后果.因此,对施工过程中的地表沉降进行预测尤为重要.

实际施工时,仅凭盾构机并无法获得对地表沉降的准确计量,需要借助施工队在地面进行测量,而人为因素造成的数据不准确时有发生.为了便于盾构租赁方掌握盾构施工状况,督促施工队按照规章制度施工,也需要能够掌握地表沉降情况.本文提出的基于排土量与注浆量的盾构施工地表沉降预测方法,通过对Peck公式的推论,可以不借助施工队测量，直接根据施工中盾构本身获取的参数对地表沉降进行预测.

在盾构施工引起的地表沉降预测领域,Peck教授取得了重大成就.他提出了用于预测地表沉降的Peck公式[1],并提出地层损失的体积与地表沉降槽的体积相等.Chakeri等[2]在研究采用土压平衡盾构机施工的地铁隧道的地表沉降时,提出隧道的直径、刀盘端面压力和最大沉降处的表面支撑力是影响地表最大沉降的3个因素.薛晓辉等[3]经过现场监测结果的验证,认为Peck公式适用于黏土层和砂岩层中的盾构隧道沉降预测.方恩权等[4]将插值法、最小二乘法和Peck公式相结合,并以广州地铁在建隧道为例验证了方法的有效性.江杰等[5]采用回归分析法并引入修正系数得到了更加准确的预测结果.范思遐等[6]提出的基于多核模式的预测方法，在提高预测精度的基础上又提高了泛化性能.

1 理论分析

本文提出的对隧道盾构法施工造成地表沉降预测的方法,是在Peck公式的基础上进行推导所得出的,以下将对此方法的理论分析进行说明.

1.1 Peck公式

在国际土力学地基基础墨西哥会议上,Peck教授提出了地层损失的概念,同时给出了估计由于隧道施工而引起的地表沉降值的方法.Peck在对大量地表沉降实测数据进行分析后,认为地表沉降槽的形状近似于概率论中的正态分布曲线,并且给出了沉降槽的宽度和不同地层条件、隧道直径及埋深等参数间的无量纲关系式.Peck公式如下:

(1)

式中:x为距离隧道中心的水平距离，m;S(x)为横断面上与隧道轴线的水平距离x的监测点的沉降量，mm；Smax为横断面的最大沉降量，mm;i为沉降槽宽度系数.

Smax的计算如下:

(2)

式中:Vloss为由于隧道开挖引起的单位推进距离的地层损失，m3/m.

i的计算如下:

(3)

式中:Z为覆土厚度，m;φ为土体内摩擦角加权平均值(°).

假定地表沉降槽的体积等于隧道施工中产生的地层损失的体积,那么横断面上的沉降曲线形状是正态分布曲线(见图1).

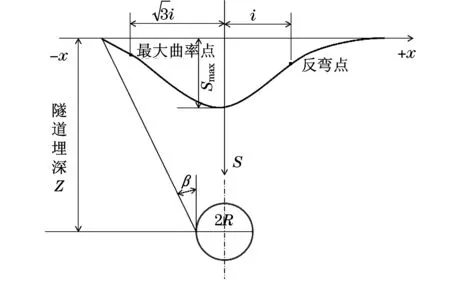
图1 Peck法地表沉降曲线Fig.1 Peck ground settlement curve

1.2 对Peck公式的推论

由于Peck提出沉降槽曲线在两个反弯点中间的区域近似于正态分布,故现有的大多数地表沉降预测方法都是借助于外因测量几个位置的沉降值,而后对正态分布曲线进行拟合.例如Peck公式回归分析[7],首先对Peck等式两边取对数:

(4)

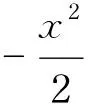
(5)

由于有测得的几组地表沉降数据,原问题从而转化成一个线性回归问题,回归得到a和b的值后便可得到最大地表沉降值.

但是实质上该方法只是单纯的对公式两边取对数后做了线性回归,本质上是使用地面测点测得的为数不多的几个数据来拟合曲线的方程.实际情况是盾构租赁方往往并非施工方,很难直接获得借助外因测得的这些地表沉降数据,这就给盾构提供方想要掌握包括地表沉降值在内的施工队施工情况造成了很大困难.

以下将给出对Peck的另一种推论方式：

地层损失量=实际的排土体积-管片外壁所占的体积-实际的注浆量,即

(6)

式中:Ve为单环排土体积;Vd为管片外径所对应的体积;Vg为单环注浆量;l为管片的长度.代入式(2)得

(7)

分析式(7)可知,只要确定了单环排土量和单环注浆量,就能脱离以施工方为代表的外因测量,对最大地表沉降值进行预测.

2 测量方法

本文所提出的方法关键在于排土量和注浆量的测量,只有获取这两个重要数据才能实现最大地表沉降值的预测,以下将对这两个数据的测量方法进行说明.

2.1 排土量测量方法

由于盾构施工时排土的形状是不规则的,想要直接得到准确的排土体积难度很大.因此,考虑采用通过测量排土质量的方法，近似得到排土的体积.

电子皮带秤是一种动态测量皮带输送机上散料质量的称重设备,考虑施工现场实际情况,在盾构机顶上的皮带运输机上安装皮带秤,如图2所示.皮带秤的秤架安装在皮带运输机的支架上,通过将皮带运输机的托辊撑起,利用称重传感器测量皮带秤上土的质量.再通过积分法，根据皮带运输的速度和在皮带秤上土的质量，得到总的排土质量.

图2 电子皮带秤测重装置Fig.2 Electronic belt scale

所谓积分法就是连续测量称重托辊上单位皮带长度载重值,并将其与同一时刻皮带速度值相乘,所得乘积就是排土的瞬时流量，即

(8)

式中:Q(t)为排土的瞬时流量，kg/s;q为单位长度载重值，kg/m;v为皮带速度，m/s.

由于皮带上的土分布不均匀,皮带速度值也有变化.因此,总质量应该是瞬时流量对时间的积分,即

(9)

2.2 注浆量测量方法

目前，盾构施工注浆量测量的主要方法是用注浆泵的单次冲程与注浆活塞面积相乘得到单次的注浆量,累计注浆泵活塞往返运动的次数来计算累计注浆量，即

(10)

式中:Q为注浆总量;n为活塞往返次数;L为注浆泵单次冲程;S为注浆活塞的横截面积.

但是这种方法认为只要活塞运动便是有效的注浆,而没有考虑到在实际注浆过程中存在吸空和回流的情况.因此,这种方法的误差较大.

针对上述由于无效注浆量带来较大误差的问题,对注浆量测量方法进行改进,如图3所示.通过一个拉绳位移传感器测量注浆泵活塞的位置,再通过一个压力传感器测量注浆泵出口处的压力,设定一个有效注浆压力值作为判断本次注浆是否有效的依据.当注浆泵出口压力小于有效注浆压力值时,判定本次注浆泵活塞往复运动吸空,属于无效注浆;当注浆泵出口压力大于有效注浆压力值时,判定本次注浆泵活塞往复运动属于有效注浆.通过高速采集拉绳位移传感器和压力传感器的值,进行积分法运算,从而得到具有更高精度的注浆量[8].

图3 有效注浆量测量装置Fig.3 Effective grouting measurement device

以该采集方法为思路,设第i个采样周期的起止时刻分别为ti1和ti2,起止时刻拉绳传感器的长度分别为li1和li2,在该采样周期内的注浆量为Qi,拉绳传感器的增量为Δli,压力传感器的压力值为Pi,有效注浆压力值为P,注浆活塞的横截面积为S.

第i个采样周期内拉伸传感器长度增量为

(11)

式中:li2-li1<0为活塞缩回,不进行注浆.

第i个采样周期内注浆量为

(12)

将包含有n个采样周期的时间段T内的Qi累加,便可获得这个时间段内的总注浆量,即

(13)

3 实际应用

以上海市某盾构法隧道施工区间为例,盾构区间地质详细情况如图4所示.该区间盾构掘进主要涉及第④1层、第④2层和第⑤2层,其中,区间盾构将有约90 m全断面位于⑤2层砂质粉土内.本次施工所使用盾构外径为6.34 m,隧道顶埋深在8.55～15.12 m之间.

图4 区间工程地质剖面图Fig.4 Engineering geologic sections

由于盾构刀盘对应的管片环数与盾尾注浆对应的管片环数相差8环左右,因此,盾构机出土的时候,对应的注浆是在其后面8环左右.结合盾构施工中所获取的数据可知,盾构机的刀盘位置从829环推到830环对应的时间是3月12日的20时40分到22时30分,而当盾尾注浆位置从829环到达830环对应的时间是3月14日的02时40分到04时25分.第830环管片处对应的盾构机处于第④2层,土体内摩擦角为22.5°,隧道埋深为12 m.

由式(3)可以计算得出沉降槽宽度系数为

根据采集的出土量数据可知,3月12日20时40分到22时30分的出土质量为

由于皮带机的称架上有泥土,导致空转时的流量达到36 t/h,这段时间内皮带机运行了35 min,因此,精确的出土质量为

根据现场勘查,排土的重度取20 kN/m3,据此得到第830环大致的出土体积为

通过采集的3月14日02时40分到04时25分的两路注浆量数据,得到第1路注浆量为2.343 m3,第2路注浆量为2.544 m3,总共的注浆量为

管片的外径为d=6.2 m,长度为1.2 m,由此可得管片外径所对应的体积为

则该环的土体损失为

代入式(7)可得预测的地表最大沉降量为

经过现场实际测量人员的测量,在隧道的第830环处的最大沉降量的变化曲线如图5所示,其稳定值在0.086 m左右.可见,该方法能够脱离施工队的测量而较为精确的对最大地表沉降量进行预测.

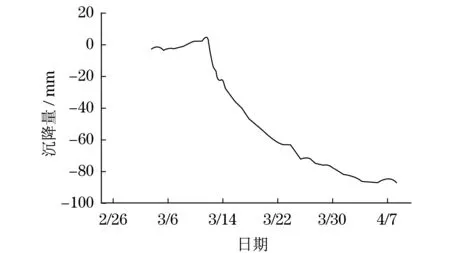
图5 第830环实际沉降量变化曲线Fig.5 Settlement curve of 830 ring

4 结论

本文提出了一种基于排土量与注浆量对盾构法隧道施工最大地表沉降值进行预测的方法.该方法通过对Peck公式的推论,能够脱离施工方现场测量等外因,直接凭借盾构机本身采集的数据对地表沉降值进行预估,从而使得盾构租赁方能够间接监控施工队操作、掌握施工质量情况以及对地表沉降这一重要数据做出主观判断.同时,本文给出了通过电子皮带秤动态测量皮带输送机上散料质量,并用积分法切片累加的排土量测量方法,以及通过拉绳位移传感器和压力传感器甄别注浆有效性的注浆量测量方法,使得所提出的地表沉降预测方法的实现成为可能.最后通过上海市某区间实际运行测量试验,验证了本方法能够较为准确地对盾构施工最大地表沉降值进行预测,是一个行之有效的方法.