一个有关椭圆问题的再探究
2018-10-30 09:06福建省仙游华侨中学351200
中学数学研究(江西) 2018年10期
福建省仙游华侨中学 (351200)
黄美琴
文[1]对一道有关椭圆问题进行探究,得到了“椭圆和双曲线共有的一个有趣而优美的结论”. 读后颇受启发,但觉得意犹未尽,可以进一步探究下去.
一、结论再现
文[1]中结论2(其中结论1是结论2的特例)、结论4(结论3是结论4的特例)是有关椭圆短轴端点与焦点的一个关联性质,本文拟对这一性质进行再探究.先把文[1]的结论2、结论4综合如下:

二、纵向再探:由特殊到一般的探究
在上述结论中,A、B为椭圆E短轴的两个端点,即直线x=0与椭圆E的两个交点,如果把直线x=0放宽为定直线x=m(c≠|m| 由此可把上述结论1推广为 特别地,当m=0时,结论Ⅰ即为上述结论1. 由于双曲线的虚轴与双曲线没有交点,所以文[1]没有给出双曲线类似于上述结论1(即文[1]结论2 、4的综合)的性质. 其实,没有交点并不影响,类似结论1,容易得到 上述结论的证明可仿照文[1]的结论2、4的证明,本文从略. 至此,我们自然要问:结论I能否推广到双曲线的情形? 由此,上述结论Ⅰ可以推广到双曲线的情形. 再看抛物线,由于抛物线只有一个顶点,所以无法给出类似于上述结论Ⅰ(即文[1]结论2 、4的综合)的性质,那么,结论Ⅰ能否推广到抛物线的情形? 由此,上述结论Ⅰ也可以推广到抛物线的情形. 至此,我们完成了对文[1]的结论2、4的再探究,得到了文[1]的结论2、4的推广.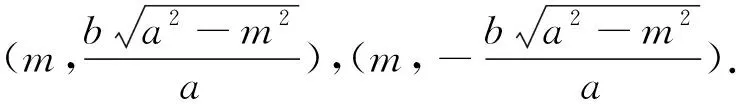







三、横向再探:由椭圆到双曲线、抛物线的探究





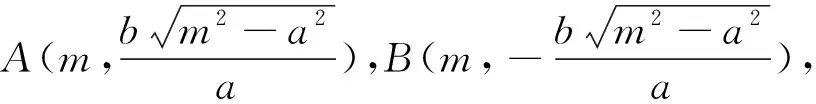





猜你喜欢
语数外学习·高中版中旬(2020年8期)2020-09-10
中学生数理化·教与学(2019年8期)2019-09-18
学生导报·东方少年(2019年7期)2019-06-11
数学学习与研究(2017年11期)2017-06-20
青年时代(2017年3期)2017-02-17
中学生数理化·教与学(2017年1期)2017-01-19
福建中学数学(2016年7期)2016-12-03
北京信息科技大学学报(自然科学版)(2016年6期)2016-02-27
理科考试研究·高中(2014年3期)2014-04-10

