立足教材夯基础 发掘联系识本质*——解一道高三模考应用题有感

江苏省苏州市田家炳实验高级中学 (215002)

王 耀

笔者最近给学生布置了一道应用题，后得知此题是2016年南京市高三数学二模测试题，命题人以直线和圆的位置关系为背景命制了一道应用题，试题设计精巧，内涵丰富，可以从多种角度进行研究，也很符合高考命题的宗旨——源于课本，高于课本，是一道颇具研究价值的好题.现将此题的解法和感受整理成文，与读者交流，欢迎批评指正.

一、试题再现

图1

如图1，某城市有一块半径为1(单位：百米)的圆形景观，圆心为C，有两条与圆形景观相切且互相垂直的道路，最初规划在拐角处(圆中阴影部分)有一块绿化地，后来有众多市民建议在绿化地上建一条小路，便于市民快捷地往返于两条道路，规划部门采纳了此建议，决定在绿化地中增建一条与圆C相切的小道AB.问：A，B两点应选在何处可使得小道AB最短.

二、思维探究

1.通性通法展示

本题常见的解题思路建立平面直角坐标系，假设直线方程y=kx+b，从直线和圆相切得到k，b之间的关系式，从而得到小道AB长度的代数表达式，转化为最值问题，即如下解法：

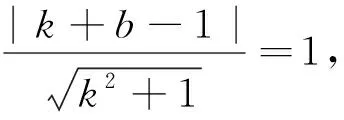
上述解法中，假设直线方程的斜截式进行计算，与标准答案相似.事实上，笔者认为若采用截距式，则更好一些，并且教材中也多次出现有关截距式的例题，这样便于计算过程中选取不同的转化方式.

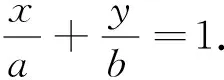
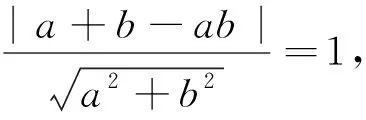
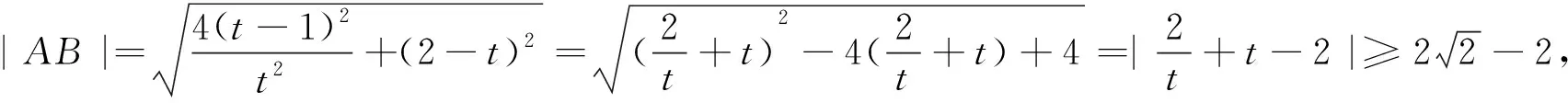
前文中的两种解法都是从设直线方程入手进行分析转化，是学生比较喜欢选用的方法；而由题意发现，直线AB是圆上某一点处的切线，故也可从圆的角度去展开分析：

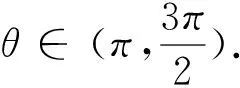
2.其它思路赏析

上面的三种常规思路都是从直线和圆的位置关系进行转化求解，偏重于代数运算，忽视了图形的功能，没有发挥出图形应有的价值，因此也可以从不同角度对图形进行思考，首先从角度关系进行分析：

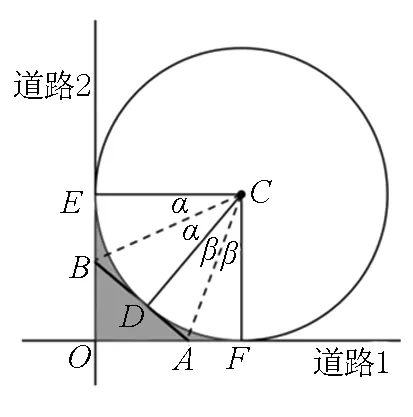
图2

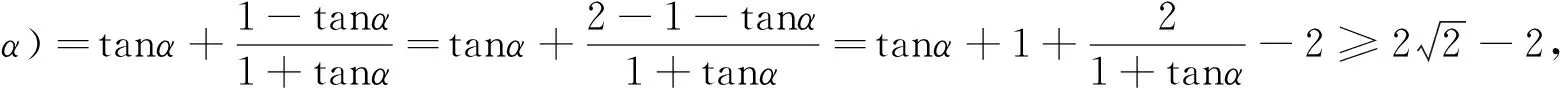
其次，还可以从边长角度去分析，利用圆的切线长相等进行联系转化，即如下解法：

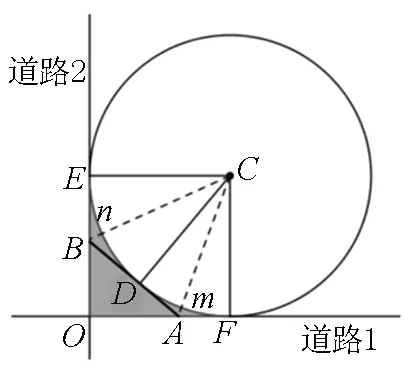
图3

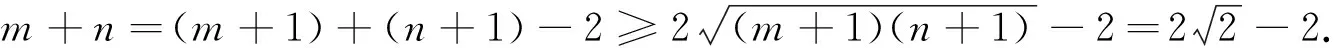
评注:由教材必修4中P115探究拓展第15题可知“当α+β=45°时，(1+tanα)(1+tanβ)=2”.因此，结合解法4和5可见，m=tanα，n=tanβ，同样得到(m+1)(n+1)=2.

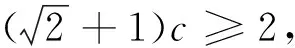
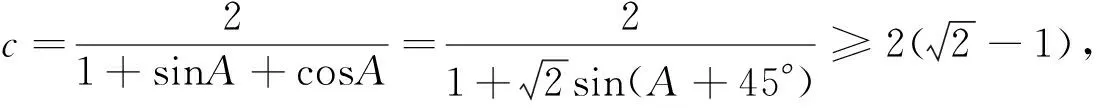
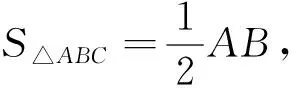
解法7:“由图可知，S△OAB=S正-2S△ABC=1-AB，只要使S△OAB的面积达到最大值时，AB最小.由Rt△OAB的周长为2，设斜边AB=c，两直角边为a，b，有a+b+c=2.

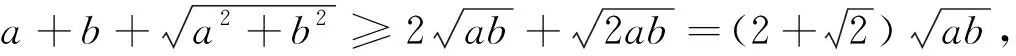
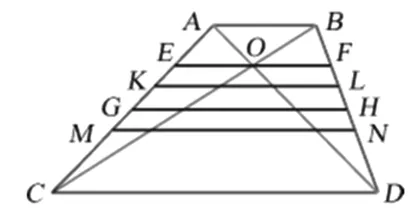
图4

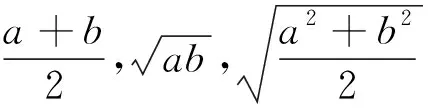
此外，在解法6中，求Rt△OAB的面积最小值时，也可以先进行减元转化为一元函数的最值问题，即结合解法2的思路进行：

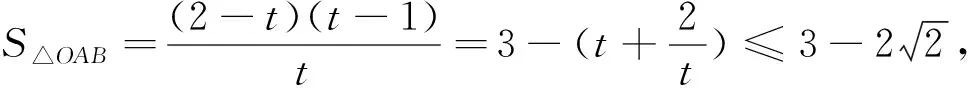
三、“似”题追溯

上文中，笔者针对这道应用题分别从解析几何、平面几何两个角度，结合了函数思想和基本不等式等工具进行了多角度分析，充分发掘了这道试题的内在联系.下面列举几道此题的类试题，供大家体会精解一道题、精通一类题的乐趣.

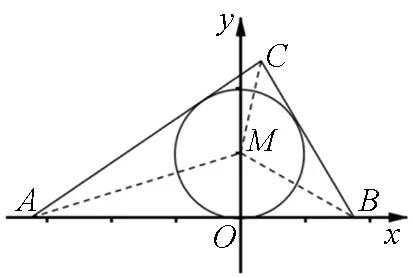
图5

(1)求圆M的方程；(答案：x2+(y-1)2=1)

(2)设A(t,0),B(t+5,0)(-4≤t≤-1)，若AC,BC是圆M的切线，求△ABC面积的最小值.

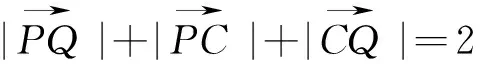
(1)试用t表示出PQ的长度,并探求△CPQ的周长；

(2)求探照灯照射在正方形ABCD内部区域的面积S的最大值．

图6

分析：试题3-1也是从直线和圆的位置关系中去研究图形中某个量的问题，原试题给出的标准答案是以由点A(t,0),B(t+5,0)着手计算直线AM和BM的斜率，再利用二倍角公式得到直线AC和BC的斜率，从而得到其直线方程和两线交点C，这是典型的解析几何思路，计算量稍大．若像解法5一样从平几角度去分析，思路更直接，计算量也适中，详解如下：

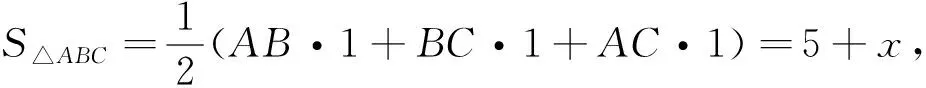
试题3-2和3-3(1)是一对互逆结论，并且通过上文中研究的解法4-解法6发现，文中研究的问题恰好是3-3(1)的一个特例，图3中正方形内45°对应的△OAB的周长为定值2，图3是利用圆的切线长关系得到，本质即为“图6中45°所对的线段PQ=DQ+PB，且以A为圆心，AB为半径的圆与PQ相切于点H，DQ=QH，HB=PB”，这个性质用初等几何知识容易证明，即：

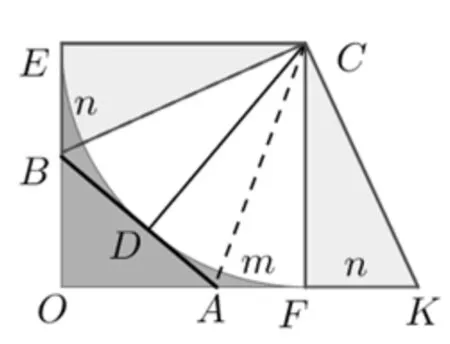
图7

“如图7，在正方形OA边的延长线上取点K，使得∠FCK=∠ECB，则易知△ACK≌△ABC，因此底边上的高CD=CF.”

若不用上述证明方法，这个结论也能通过解析法计算并得到证明：

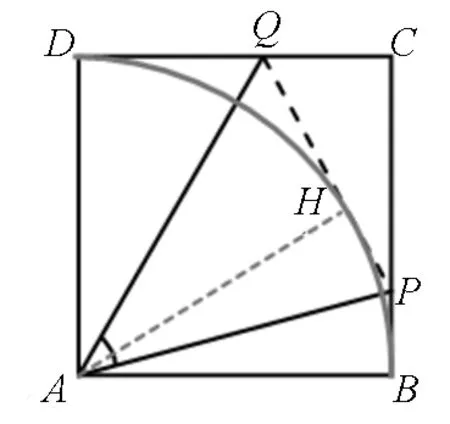
图8

“如图8，设PB=m，DQ=n，由余弦定理可知

(1+m2)+(1+n2)-[(1-m)2+(1-n)2]=

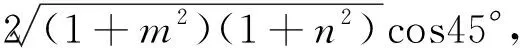
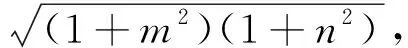
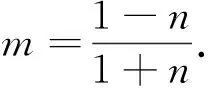
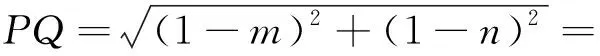
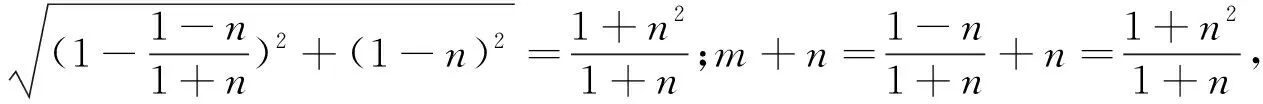
四、解后感悟

(1)教材是高考命题的基本出发点

近年来的江苏省高考数学试卷风格变化不大，试题朴实平和，大多数题目的根源来自课本，给考生似曾相识的亲切感.这其中透露的信息便是要求高考复习必须坚持回归课本，夯实基础，熟练掌握高中基本数学知识和基本数学思想.

就本文中研究的这道应用题来说，笔者根据教材相关内容入手，从多个层面进行分析，列出了与每种解法有联系的题源或方法出处，以此为线索将教材中相关知识点集中到一道问题中来，由点到面，展示了问题蕴涵的丰富内涵，充分体现了研究数学问题时带来的统一美和简洁美.

(2)教材是解题能力的根本生长点

我国著名数学教师宋庆先生认为：“学习数学的主要目的在于解题，掌握数学就意味着善于解题．”高考作为选拔性考试主要表现在解题上．而教师作为解题的示范者、引路人，首要任务就是加强解题训练、提高学生的解题能力．

因此，回归课本发掘联系，是高考数学复习的一项关键工作，在具体教学工作中，笔者建议可以从教材上选取一些典型问题进行开发，帮助或引导学生基于教材进行微专题研究，从而实现对知识框架的进一步梳理，以及对数学思想方法的更深层次的理解，这对促进学生数学解题能力的发展将是大有裨益.