解法多样，精彩呈现——广东省2018年中考数学第24题评卷分析及启示

☉广东省珠海市拱北中学 吴 岩

广东省2018年中考数学第24题，满分9分.珠海市参加考试学生17251人，平均分为1.74分，标准差为2.09，各分数段人数及比例如下：

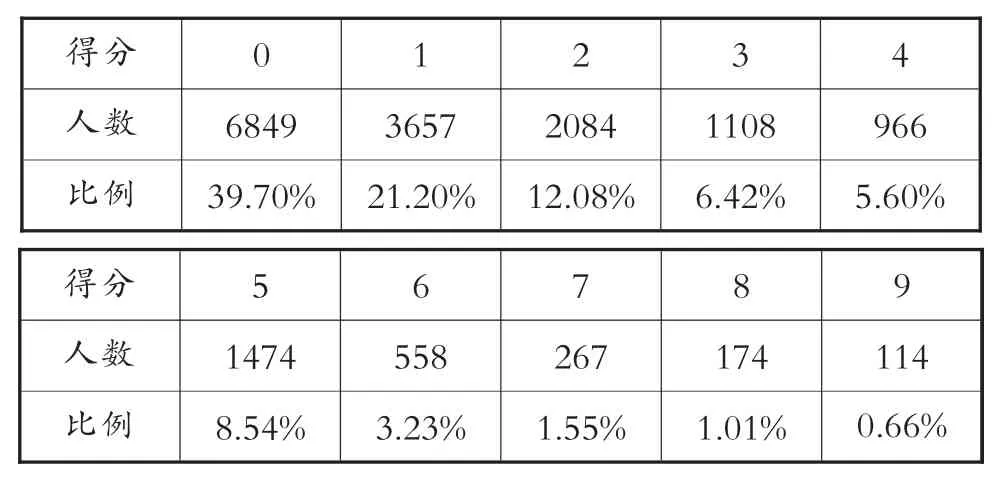
表1

原题呈现：如图1，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC、OD交于点E.

（1）证明：OD//BC；

（2）若tan∠ABC=2，证明：DA与⊙O相切；

（3）在（2）的条件下，连接BD交⊙O于点F，连接EF，若BC=1，求EF的长.

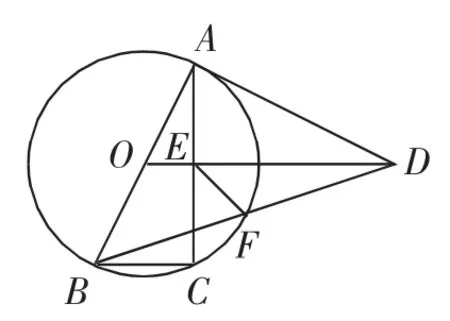
图1

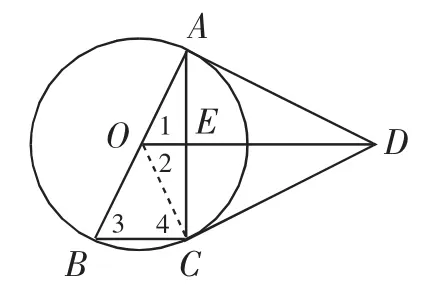
图2

一、典型解法

（1）解法1：（证两次全等）如图2，连接OC.

由OA=OC，AD=CD，OD=OD，得△AOD △COD（SSS）.

则∠1=∠2.

又OA=OC，OE=OE，则△AOE △COE（SAS）.

则AE=CE.

又OA=OB，则OE是△ABC的中位线.

则OE//BC.即OD//BC.

点评：这是最常规的一种证法，大多数学生采用这种证法.也有证完全等之后用三线合一证E是AC的中点的；也有证完全等之后用△OBC的外角∠AOC来证明∠2=∠4的；也有用圆周角定理证∠1=∠3的；也有用垂径定理证OM⊥AC的.

解法2：（利用垂直平分线的判定定理）连接OC.

由OA=OC，得点O在线段AC的垂直平分线上.

同理，点D在线段AC的垂直平分线上.

则OD是线段AC的垂直平分线.

则OD⊥AC.

由AB是直径，得∠BCA=90°，即BC⊥AC.

则OD//BC.

点评：这是最简洁的一种证明方法，但采用此法的学生不多.

（2）解法1：（全等三角形）由tan∠ABC=2，得BC=AC.

又AB=DA，则Rt△ABC Rt△DAE（HL）.

则∠BAC=∠ADE.

则∠OAD=∠BAC+∠EAD=∠ADE+∠EAD=90°.

则DA与⊙O相切.

点评：这是最常见的一种解法，但在写全等理由的时候，有部分学生写成了SAS或SSA.

解法2：（勾股定理及其逆定理）设BC=x.

由tan∠ABC=2，得AC=2x.

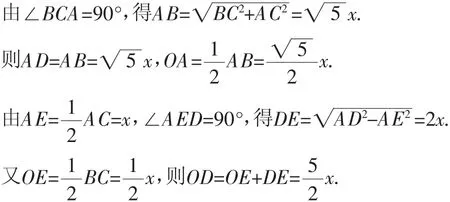
由AO2+AD2=x2=OD2，得∠OAD=90°.

则DA与⊙O相切.

点评：这种方法也有较多的学生使用.求DE的长是难点，不少学生因此半途而废.

解法3：（用三角函数）由解法2知，AE=x，DE=2x，∠AED=90°，则tan

则∠BAC=∠ADE.

则∠OAD=∠BAC+∠EAD=∠ADE+∠EAD=90°.

则DA与⊙O相切.

点评：也有用∠BAC和∠ADE的正弦、余弦三角函数证明的，方法类似.但不少学生在求正切值时使用tan∠ADE=，默认∠OAD=90°，犯了循环论证的错误.

（3）解法1：（证△DEF △DBO）由BC=1，AC=ED=2，得AD=CD=AB=

由AB=AD，AB⊥AD，得△ABD是等腰直角三角形.

如图4，连接AF，则AF⊥BD，则F是BD的中点.

又∠EDF=∠BDO，则△DEF △DBO.

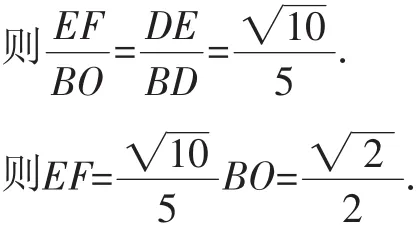
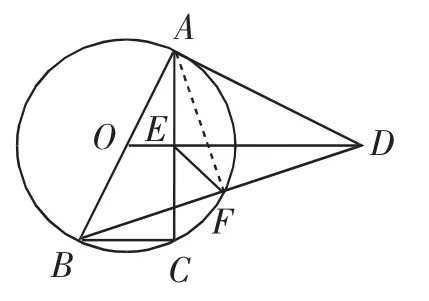
图4

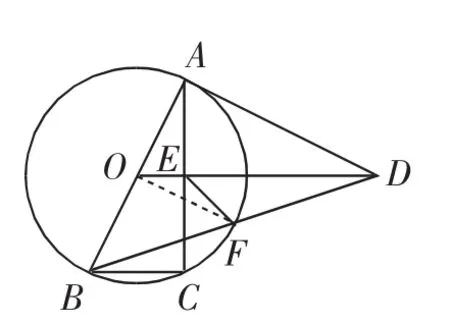
图5

点评：这是最常规的解法，大多数学生采用此种方法.也有用射影定理和切割线定理来证明对应边成比例的.因为AD2=DF·DB（切割线定理），AD2=DE·DO（射影定理），所以DF·DB=DE·DO.则

解法2：（证△OEF △OFD）如图5，连接OF，由解法1知OE=

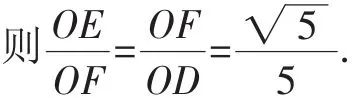
又∠EOF=∠FOD，则△OEF △OFD.

点评：与解法1有异曲同工之妙.

解法3：（证三角形全等）如图6，分别延长EF与BC，其交点记为G.

由解法1知EC=1，DE=2，F是BD的中点.

易得△EFD △GFB.

则CG=BG-BC=ED-BC=2-1=1.

则△ECG是等腰直角三角形.

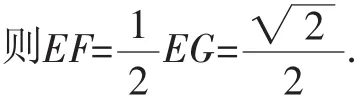
点评：构思巧妙，运算量也不大.也可以连接并延长CF与DE交于点M，类似地证明△CEM是等腰直角三角形，可得，参见图7.

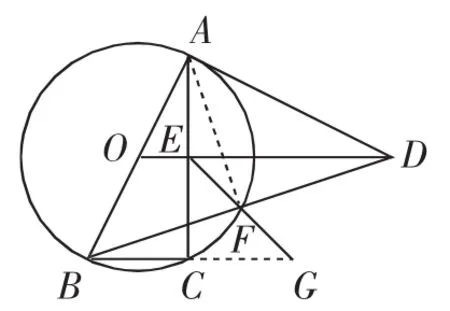
图6

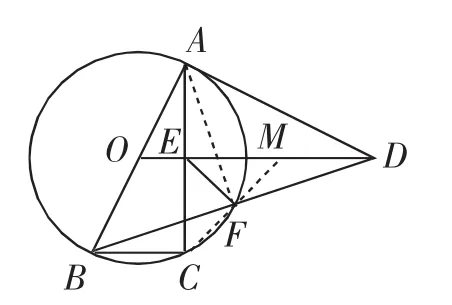
图7

解法4：（利用全等证等腰直角三角形）如图8，由解法1知△ABD是等腰直角三角形，F是BD的中点，AF=BF=DF，AE=BC=1.

又∠CBF=∠EAF，则△CBF △EAF.

则CF=EF，∠EFA=∠CFB.

则∠EFC=∠CFB+∠EFB=∠AFE+∠EFB=∠AFB=90°.

点评：也可以用∠ABF=45°证明∠EFC=90°.具体如下：由∠ABF=45°，弧AF=弧AF，得∠ACF=∠ABF=45°.又CF=EF，则∠FEC=∠FCE=45°.则∠EFC=90°.

解法5：（利用弦切角求CF）如图8，AF与DE的交点记为K.

在△AEK和△DFK中，∠AKE=∠DKF，∠AEK=∠KFD=90°，则∠EAK=∠KDF.

又由解法1知FD=AF，ED=AC，则△CAF △EDF.

则EF=CF.

易知CD是⊙O的切线.

则∠FCD=∠CBD（弦切角定理）.

又∠FDC=∠CDB，则△FDC △CDB.

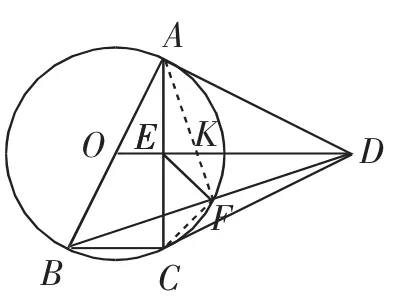
图8

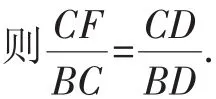
点评：这是直接求CF长度的一种方法.

解法6：（证△ABC △OFM）如图9，过点F作FM⊥OD，垂足为M，连接AF、OF.

OF是△ABD的中位线，则OF//AD.又AB⊥AD，则AB⊥OF.

由∠1与∠2互余，∠2与∠3互余，得∠1=∠3.

又∠ACB=∠OMF，则△ACB △OMF.

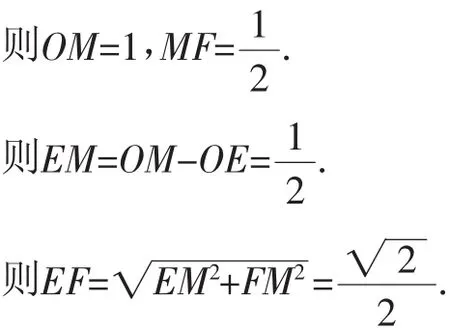
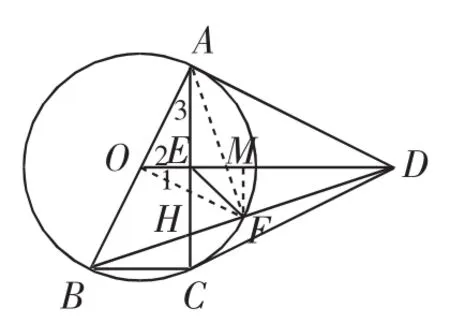
图9

点评：注意到AO=FO，可得△AOE △OFM，也能求EF的长.解法4～解法6揭示了图中三组关键的全等三角形.本解法也可以不证全等，不证相似，直接设OM=x，则MD=-x， 利 用OF2-OM2=MF2=DF2-MD2， 列 方 程

解法7：（证两次相似）由解法1知EC=1，ED=2，FD=

如图10，过F作FM⊥MD.

易得△MFD △CHB.

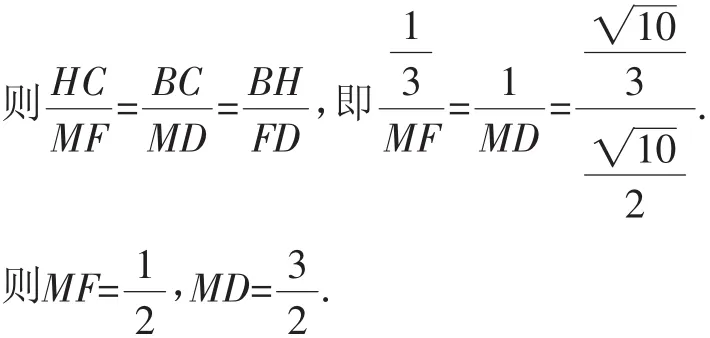
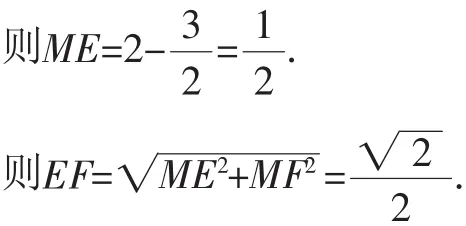
点评：该证法是步骤较多，运算量较大的一种方法.

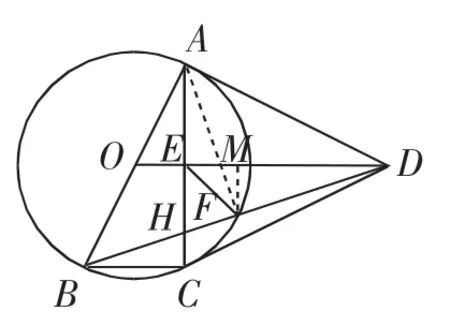
图10

图11

解法8：（构造矩形）如图11，过点D作DP⊥BC与BC的延长线交于点P，过点F作FM⊥OD，垂足为M，MF的延长线与BP交于点N.

易知四边形ECPD、四边形ECNM、四边形MNPD都是矩形.

由解法1知ED=2.

则BP=BC+CP=BC+ED=1+2=3.

由解法1知F是BD的中点，则FN是△BPD的中位线.

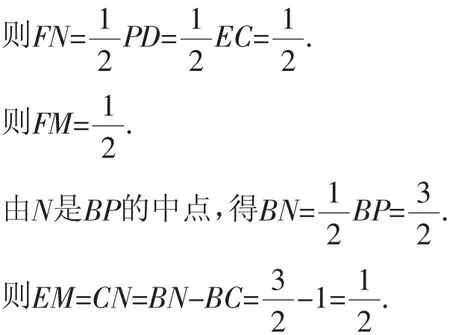
点评：也有的过点B作BP⊥OD，同理可以求EF的值，参见图12.

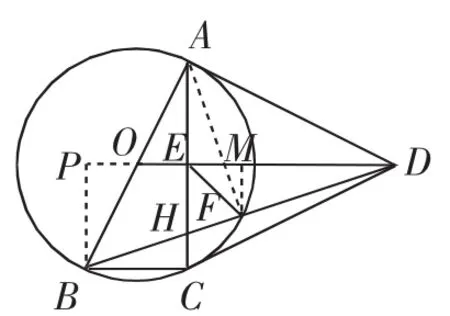
图12

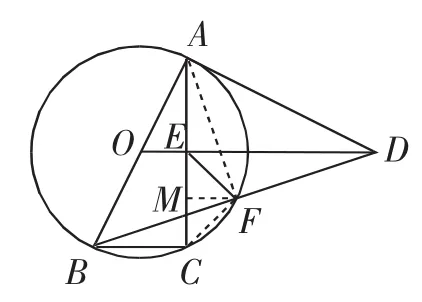
图13

解法9：（平行线分线段成比例定理）如图13，过F作F M//ED交AC于M.

易知MF⊥EC，BC//FM//ED.

由F是BD的中点，得M是EC的中点.

由∠FCA=∠FBA=45°，得∠MFC=45°.

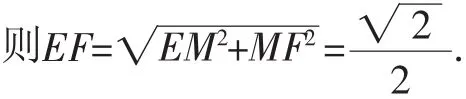
点评：这是一种比较简洁的证明方法.

解法10：（面积法）如图14，过E作EQ⊥BD，垂足为Q，连接BE、AF.

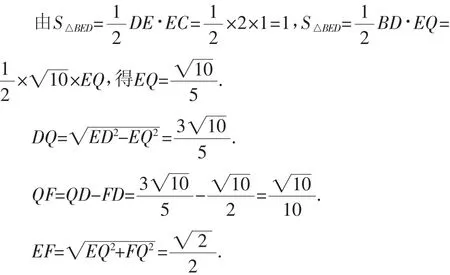
点评：构造普通的直角三角形求EF.另外一种类似的方法是：连接AF，过E作EM⊥AF，垂足为M.△AHF的三边较易求得，AE=1，△AHF △AEM，可得EM、AM、FM的长，于是.参见图15.

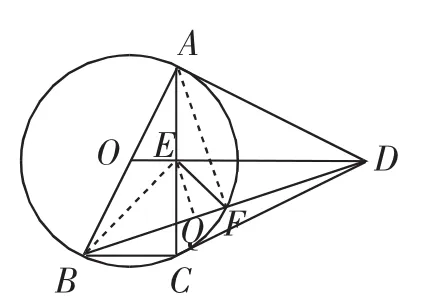
图14

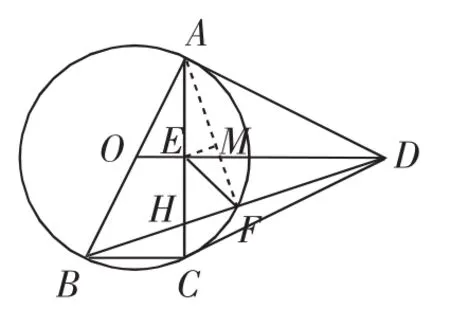
图15

解法11：（构造中位线）如图16，连接BE、AF，过点B作BM⊥BE，与DE的延长线交于点M，连接BM.

则EF是△BDM的中位线.

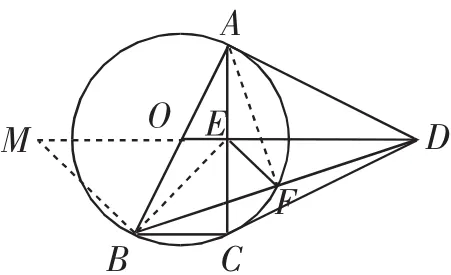
图16

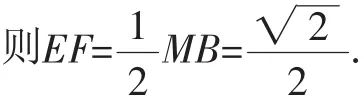
图17

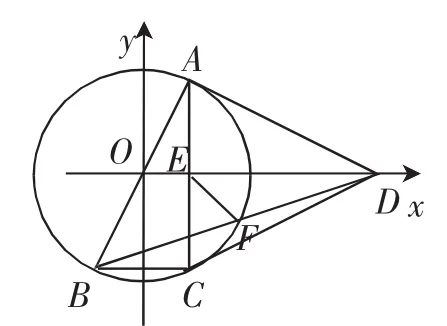
图18

点评：解法11是众多解法中，思路最简洁、运算量最少的一种方法.也可以连接并延长BE至M，使得EM=EB，连接MD，类似地证明，参见图17.

解法12：（建立平面直角坐标系）如图18，以O为原点，建立平面直角坐标系.

点评：也可以先证F是BD的中点，用中点公式求得F点的坐标.

二、解法分析

上述第（3）问的12种解法显示EF的长度可以通过这样几种方法求得：（1）构造相似三角形；（2）构造等腰直角三角形；（3）构造普通直角三角形；（4）构造中位线；（5）解析几何的方法.

三、典型错误

1.思路不通

第（1）问中，不少卷子是空白的，系统显示本题0分卷有6849份，占39.70%.主要原因是，不会添加辅助线，没有头绪，无从下手.

2.编造条件

第（1）问中，不少学生知道要证全等，但在没有预先证明的情况下，编造∠ADO=∠CDO，用SAS证明.

3.循环论证

第（2）问在未证明∠OAD=90°的情况下，直接用三角函数，犯了循环论证的错误.

4.方法使用不当

5.使用错误的判定定理

6.证不出，直接使用

第（2）问，不少学生想证△DEF △DBO，但只有∠EDF=∠BDO一个条件，于是不少学生编造出∠FED=∠OBD，继续证明下去.

四、教学建议

1.夯实基础

该题有39.70%的0分卷，主要是因为解第（1）问时没有思路，无从下手.表明这些学生基本功较差，辅助线都不会连.也有不少学生连了辅助线但不会用SSS证三角形全等，甚至∠BCA=90°也无从知晓.

作为教师，在教学上要重视“四基”教学.一方面，要重视基础知识、基础技能的教学.证三角形全等是初中几何的核心内容，必须花大力气落实全等的判定方法，使学生能了如指掌，熟之又熟.对于圆的教学，也要提高到应有的高度，有些学校为了腾出更多的时间用于复习，压缩了初三新课的教学时间，结果圆的教学就成了夹生饭.这显然是得不偿失的，要知道圆的内容是中考高分题必考的题型.不花足够的时间，不练足量的题目，是难以形成能力的.另一方面，也要重视数学基本思想、基本活动经验.只解题不反思，只做题不总结，永远只是知识的搬运工，做不了知识的主人.解题的过程是学生理解知识、体验基本活动经验的过程，但必须不断反思与总结才能形成解题思想.只有这样，在面对较为复杂的几何题时，才能从容不迫.

2.重视细节

几何证明是根据已知和结论，写出推理过程的一种题型，所以过程甚于结论.在答卷中，不少学生随意编造理由，没有证明就直接使用，循环论证、虚假论证等情况大量存在.要杜绝此类问题，在平时的教学中，要注重细节.（1）审题要细心.知道哪些是可用的条件，哪些是不可用的条件，哪些是直接使用的条件，哪些是证明了之后才可以使用的条件.（2）表达要严谨.不使用错误的判定方法，不编造条件，杜绝跳步证明.（3）及时总结.常见的辅助线的添加方法，常见的几何模型，常用的解题思想都要及时归纳总结，使之成为知识的储备.

3.开拓思维

第（3）问乍看十分困难，但实质上解法多样，仅考场做法就有12种.思路就是出路，在考场上学生要敢想敢试.在实际的教学中要重视一题多解.（1）一题多解可以培养思维的广阔性，拓展解题的方法、方式.在第（3）问中，EF的求法很多，既可以构造相似三角形，又可以构造直角三角形，还可以构造中位线.（2）一题多解可以深化对问题的理解.仅仅只看一种解法，对题目的认识是不够的.以第（3）问为例，多尝试几种方法之后才发现F点的位置很特殊，是两个等腰直角三角形斜边上的中点，这种特殊的位置造就了多样的解法.