“商不变的规律”教学断想

朱勇

摘要：“商不变的规律”要注重研究被除数和除数在怎样的情况下商不变的本质联系。一般来说，科学研究过程有四个步骤，即提出问题一做出猜测一寻找证据一得出结论。“商不变的规律”教学，根据实际情况将规律的探究过程细化为疑问、猜想、验证、归纳、完善、应用、新疑问，打造一个不断螺旋上升的学习过程。

关键词：商不变的规律 教学 数学思维

执教苏教版小学数学四年级上册《商不变的规律》，我认真思考了这样三个问题：其一，什么是商不变的规律？其二，为什么有商不变的规律？其三，商不变的规律该怎样教学？以下是针对这三个问题的相关思考及实践应答。

一、什么是“商不变的规律”

教材中关于“商不变的规律”这样写道：被除数和除数同时乘或除以一个相同的数（0除外），商不变。我们都知道商不变的规律有两个好伙伴——分数的基本性质和比的基本性质。分数的基本性质内容是分数的分子和分母同时乘或除以一个相同的数（0除外），分数的大小不变；而比的基本性质说的是比的前项和后项同时乘或除以相同的数（0除外），比值不变。让我感兴趣的是，为什么三者本质相同，商不变叫规律，而分数和比却叫性质？

关于规律和性质，《现代汉语词典》是这样注释的——“规律”：（1）名词。事物之间的内在的本质联系。这种联系不断重复出现，在一定条件下经常起作用，并且决定着事物必然向着某种趋向发展。也叫法则。（2）形容词。有规律。“性质”：名词。一种事物区别于其他事物的根本属性。我理解为“规律”的核心词是本质联系，“性质”的核心词是根本属性。联系教学的内容，也就是说“商不变的规律”要注重研究被除数、除数在怎样的情况下商不变的本质联系。所以，我这样教学——

（出示例7的题干与空表格，逐步出示：

100÷20=5，200÷40=5。）

师 你能猜到下一道算式吗？

（在学生说出不少算式后，选两道算式接

着出示：300÷60=5，400÷80=5。）

师 大家有什么发现？

生 商没有变。

师 那么商在被除数和除数怎么变化的情况下是不变的？

（学生观察思考，通过将第一道算式和下面几道算式逐一对比，得出被除数和除数乘2、乘3、乘4时商都不会变，见图1。）

生 被除数和除数乘一个数，商不变。

师 还有什么情况下商不变呢？再看一组算式。（出示：100÷20=5，50÷10=5，25÷5=5，10÷2=5。）

师 你能也做出一个猜想吗？

生 被除数和除数除以一个数，商也不变。

师 （重复刚才两个猜想的内容）谁能将这两个猜想合成一句话？

生 被除数和除数乘也可以除以一个数，商不变。

生 被除数和除数乘或者除以相同的数，商不变。

师 我们来看看书上是怎么说的，对比一下，找找有什么不同？

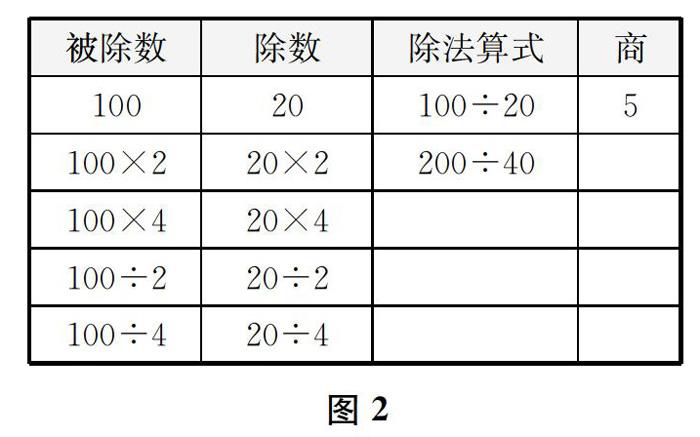
教材上的例题以表格的形式（见图2）呈现了几个算式，较明显地暗示了通过对被除数、除数的比较来揭示规律。所举算式相较于第一道算式，乘或除的数全是偶数，容易让学生产生误会。表格中的数据较多、较乱，不利于学生分类逐步思考，处理不好反而不容易突出探究重点。因此，我在把握了商不变规律的实质的基础上，舍轻就重，通过设计两组口算展开教学，联系学生已有知识，完善探究材料，明确探究方向，引导学生对商不变的规律深入探究，追根溯源，突出了“被除数、除数在什么情况下商才不会变”这一教学重点。

二、为什么有“商不变的规律”

对四年级学生而言，通过几个实例得出商不变的规律并非难事，但是仅仅依靠几道算式就得到的规律真的可靠吗？是否值得信赖？如果不把这个问题当作问题，不仅会让学生对于数学知识的理解趋于肤浅，也可能给数学学习不严谨的滋生提供土壤，因而，验证成为必然。

怎样验证呢？教材是这样要求的：“自己再找一些例子，算一算，比一比，看商有没有变化。”显然，这是符合学生实际的。合情推理是第二学段对学生数学思维发展的一般要求。在大量例子面前，刚刚得出的猜想能不能够通过考验，能则说明猜想的正确性，反之则错误。但是商不变的规律僅靠举例子让学生通过合情推理的方式验证就可以了吗？还可不可以有其他方式？

四年级学生的数学思维已经具有了一定的发展水平，适度提高要求，让他们用更加理性的思考解决问题，既具备了可能的前提，也具备了实践的可行性。因此，教学时我带领学生再往前探一探——

师 同学们，你能验证商不变的猜想吗？可以先举些例子，再想想不举例的话，有没有其他办法来验证？（学生验证，教师巡视，寻觅一些可以展示的素材。指名使用其他方法的学生展示他们的方法。）

生 20×5=100，100÷20=5，40×5=200，200÷40=5，…。（解释）乘法中一个乘数不变，另一个乘数乘几，积就乘几。乘法反过来就是除法，乘数不变就是商不变。

生 被除数和除数同时乘同一个数，乘的那个数会互相抵消，所以商不变。比如，被除数和除数同时乘2，两个2就互相抵消了，所以商不变。

（教师配合板书，如图3，帮助学生理解。）

验证是理性思维培养的极佳手段。虽然合情推理能够得到结论，但是并不应满足于此，可引导学生应用多种方式，尤其是暗含演绎推理的方式（如连除的计算规律）进行证明，从而让学生的数学思维更加缜密、严谨。这样的教学，不仅让学生明晰知识间的紧密联系，了解彼此间的互相转化，还能从知道商不变的规律迈向理解为什么有商不变的规律，不仅知其然而且知其所以然。其实，其他版本教材中就有类似的设计：人教版小学数学教材在出示商不变的规律之前先向学生展示了除数不变和被除数不变的规律，便于学生了解这些规律之间的联系；沪教版小学数学教材出现了除法中连除的性质，并用字母表示了出来，以帮助学生验证商不变的规律。

三、“商不变的规律”该怎样教学

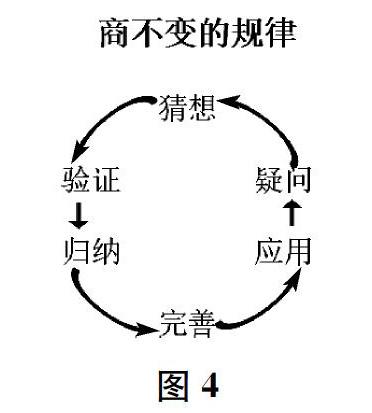
数学是一门科学，研究过程应当与科学的研究相一致。一般来说，科学研究过程有四个步骤，即提出问题一做出猜测一寻找证据一得出结论。本节课，我根据实际情况将规律的探究过程细化为疑问、猜想、验证、归纳、完善、应用、新疑问，意在打造一个螺旋上升的学习过程。为了给学生这样的认识，我尝试这样教学——

（出示口算题：80÷20，320÷80，450÷90，140÷7。）

师 你们怎么算得这么快，能以一道题为例说一说吗？

生 算320÷80时，我想32÷8=4，所以320÷80=4。

师 我产生了一个疑问，真的可以这样算吗？（板书：疑问。接下来，沿着“猜想、验证、归纳、完善、应用”的路径带领学生一起研究，一起学习。课堂尾声，教师和学生展开回顾总结，适时在关键词之间连上箭头，形成封闭图形的板书，如图4。）

师 同学们，本节课我们学了商不变的规律，你还有没有疑问？

生 其他运算中有没有这样的规律？

师 带着这些疑问，我们又可以开始新一轮的猜想、验证、归纳、完善的循环，这就是科学家、数学家研究问题的常用过程。

图4既是板书，也呈现了科学研究的一般过程，目的是让学生通过本课的学习，达到学习其他规律或者知识时能主动使用这样的研究路径，学会学习，做学习的主人。规律的认知不仅仅是规律本身，更要让学生经历探究规律的过程，学生只有全程参与，才能积累研究经验，获得真实的知识，发展数学思维。