运用相关思维对一道中考压轴题的教学观察

☉湖南省常德芷兰实验学校初中部 陈金红

一年一度的中考数学压轴题，既是命题者头痛的“磨难”命制，更是考生心有余悸的“伤痛”.如何在紧张的考场有效轻松应对，研究中考压轴题就是一件必不可少的实践活动，为此我们对湖南省常德市2018年的数学压轴题第26题做教学剖析，希望我们的教学观察能为同仁带来一点黎明曙光：

题目 已知正方形ABCD中，AC与BD交于O点，点M在线段BD上，作直线AM交直线DC于E，过D作DH⊥AE于H，设直线DH交AC于N.

（1）如图1，当M在线段BO上时，求证：MO=NO；

（2）如图2，当M在线段OD上时，连接NE，当EN∥BD时，求证：BM=AB；

（3）如图3，当M在线段OD上时，连接NE，当NE⊥EC时，求证：AN2=NC·AC.

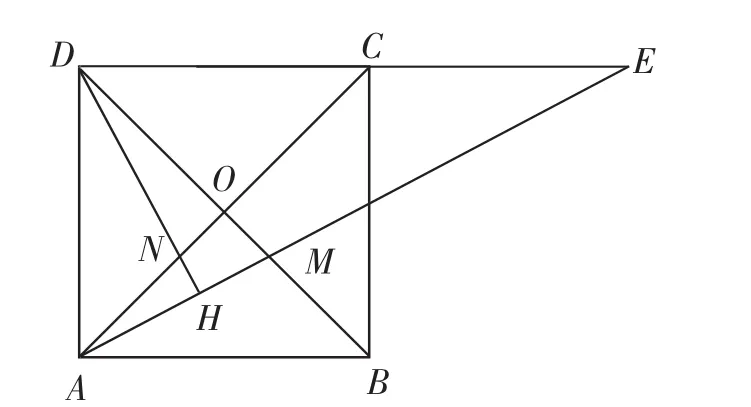
图1

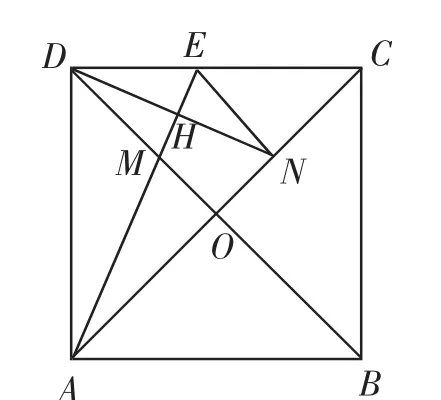
图2

图3

一、涉及考点

（1）特殊图形：正方形、等腰三角形、直角三角形等；

（2）几何性质：正方形的性质、直角三角形的性质、相似三角形的性质与判定、全等三角形的性质与判定、线段垂直平分线定理等；

（3）可以运用的选学内容：四点共圆、圆幂定理、射影定理等.

二、基本解析

三个小问题的提出是基于点M在正方形对角线BD被对角线交点平分线段的不同位置所引起，其实隐喻“动点M”乃问题之间的思维联系纽带！

第（1）问主旨是考查两个直角三角形的全等的运用，条件一是有一对相等的直角、条件二是一对相等的锐角（由同角（或等角）的余角相等得出的）、条件三是一条直角边相等（由正方形对角线相等互相平分性质得到的）；具体判定方法是“ASA”或“AAS”推出：△OAM △ODN，从而有MO=NO.

第（2）问，当点M运动到OD上时，同理仍有△OAM△ODN，从而仍有MO=NO.由此可得到许多相等的线段，比如EM=NC、BM=AN等.

同样也有许多的全等三角形，比如△ADM△DCN、△BAM △ADN等.还有许多的相似三角形，比如不连线时的△DME △BMA，△CEN △CDO，Rt△HDE、Rt△HAD与Rt△DAE三个三角形也相似（直角三角形重要性质——射影定理），若连辅助线MN有△OMN△ODC等；见图4.综合上面的信息平行四边形MNED；又已知DH⊥AE于HN，即AH是DN的垂直平分线⇒AN=AD.而AB=AD，BM=AN，于是有AB=BM.继续演绎下去会有更多的全等三角形和相等的角和线段（略）.

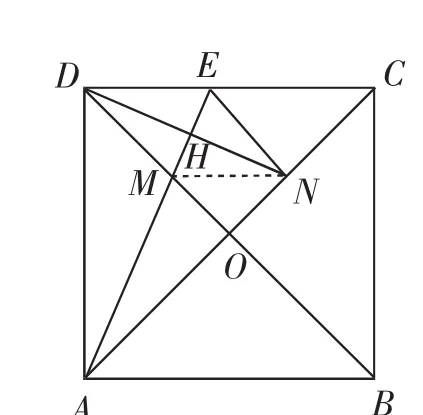
图4

图5

三、教学观察

⒈题目设计：蕴藏思维定式与圈套障碍点

对于第（1）问，属于基本常规给分点，很容易上手，乃激发答题者的兴趣和解题斗志的设计；

对于第（2）问，考生很容易纠缠于想通过证明∠BAM=∠BMA去证明线段AB=BM，其实是一个死胡同！显然跳出这个设计的“定式思维”最明智的方法是像上面的分析一样发散开来！

对于第（3）问，若从NE⊥EC、AD⊥DC⇒EN∥AD出再推理演绎的话也会出现死胡同！或利用直角三角形射影定理模型法展开推理仍会出现死胡同！跳出这个设计的“思维”圈套最明智的方法也就是上面说的信息发散！

2.题目检测：考生数学思维的长度与解题能力

显然要一气呵成解决这些问题，从显性的图形与已知出发，先做基本的演绎推理得出隐形的一些相等的角、相等的线段、全等的三角形、相似的三角形，再两两组合得出新的相等的角、相等的线段、全等的三角形、相似三角形，即发散更多的隐形的数量、位置和变换关系.这些无不体现出考查知识的覆盖度、思维的连贯性和逻辑的严谨性！

3.解题方法：亦可合情推理，拼凑法朴素轻松

显然严格推理不是一件在规定时间内轻松解决的事情，咋办？根据新的课程标准和数学学科核心素养的基本要求，不妨合情推理展开思维：直接计算推理，即：

①等腰Rt△NEC中，NC2=2NE2；②Rt△NED中，NE⊥DE、EH⊥DN于H⇒NE2=NH·ND（射影定理）.联合知NC2=2NH·ND.

③∠DHA=∠DOA=90°⇒四点D、H、O、A共圆⇒NH·ND=NO·NA.

4.思维模式：暗含提纲挈领的纽带

显然生活中一个事件常常引发多个相关事情的发生（多米诺骨牌效应），映射到数学命题中来，利用几何变换如一个点的运动，与定点相关联得到一个图形如线段就会是动线段，产生“子母”联动形象，于是相关思维的有机破解能力就自然被要求了！本题的一个动点就是正方形ABCD的对角线BD上的点M，与定点A相连的线段AM就是动线段，于是相关联的其他图形就受其制约了，于是“动点M”乃问题之间被“提纲挈领”的思维联系纽带！这正是我们研究中考压轴题教学观察的结论：找到“相关思维”被“纲举目张”的思维动点，为我们的解题指明前进的方向！