放飞思维 收获智慧

☉江苏省常熟市梅李中学 王伟春

迎合“考点”而进行的知识概览、基础回顾与重点强化是初中数学复习教学惯常采取的三个重要步骤，如何处理好夯实基础和提升能力、课堂容量和思维深度、旧知重提和激发兴趣之间的关系成为教师最为关注的问题.笔者认为，复习教学应紧扣主题并巧设问题情景，使学生能够在层层递进的问题探索中获得思维的飞速发展与突破，并因此获得高质高效的复习效果.本文结合“一次函数”这一案例对促进学生思维发展的教学作一定意义上的思考和探究.

一、案例概述

1.寓言引思

假设兔子与乌龟在赛跑时都是匀速前进的，行走的路程与时间分别为s（m）、t（min）.

问题1：s和t之间关系的图像怎样？请尝试作图.

学生不断思考并尝试着作图.生1在黑板上画出了图1所示的OA、OD两条射线，其他学生不禁发出了质疑，生2随即将图像进行了补充.

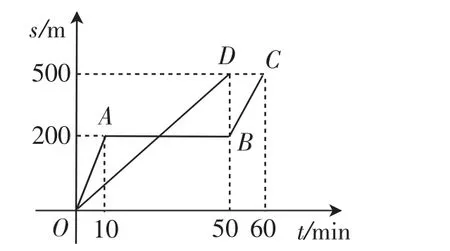
图1

问题2：你在给出的数据中感受到了哪些信息呢？

学生纷纷发言：能求出线段OD、OA、BC之间的关系式；兔子睡觉时间为40分钟；OD、BC分别是正比例函数图像和一次函数图像；乌龟追上兔子是在什么时候？乌龟的速度是10米/分钟；兔子一开始的速度是20米/分钟……

设计意图：运用寓言拨动学生思维并将复习的重点引进课堂，学生感觉有趣的同时也感受到了函数的亲切.

2.温故知新

（1）（2）略.

（3）若一次函数y=kx+b过点（x1，y1）、（x2，y2），且k＞0，b＜0，当y1＜b＜y2时，有（ ）.

A.x1＞0＞x2B.x1＜0＜x2

C.x1＜x2＜0 D.x1＞x2＞0

很多学生因为抽象的表述而感觉思维困难.

师：大家以为此题考查的主要是什么知识呢？

众生：函数的增减性.

个别学生提出了“单调性”的回答，最终在数形结合下选出了答案.

问题3：大家能在保持结论不变的情况下改变方框中的条件吗？

生3：图像过一、三、四象限.

生4：y随x的增大而增大.

生4的观点立即遭到了大家的反对，大家认为这一条件是不能保证b＜0的.

师：大家以为结论会不会和b的符号相关呢？

生5：一次函数的增减性只会和k有关联，此题和b也是相关的.

生6：b＜0是多余的，因为不管b取何值，当y=b时都有x=0，因此只要k＞0，就有x1＜0＜x2.

大家纷纷赞同.

设计意图：渗透数形结合的数学思想并引导学生对函数的增减性加强认知.

3.典例剖析

问题4：大家可否在图2中获得一定的信息？

众生：这是一次函数的图像；y随着x的增大会减小；直线的关系式是当x＞4时，y＜0……

图2

图3

众生：不对，OA不是斜边.

师：生10的观点虽然不一定正确，但等同学们学过三角函数后就会发现，确实是所有角度都是可求的，他的观察能力很棒！

师：求四边形OABC的面积是同学们的问题中最难的，大家有哪些办法可以求解呢？

生11：S四边形OABC=S△ABE-S△COE.

师：非常好，这就是转化思想，运用规则图形的面积相加或相减来求得不规则图形的面积.

生12：S四边形OABC=S△AOD-S△BCD.

生13：过点B作BF⊥CD于点F，则有S四边形OABC=S梯形AOFE-S△CFB.

师：很好，用到了补形转化.

生14：过点B作BH⊥OA于点H，则S四边形OABC=S梯形COHB+

问题6：请大家观察图3并说说哪些问题可解.

生7：求交点B的坐标.

生8：四边形OABC的面积和所有三角形面积都可求.

生9：所有线段的长度都可求.

生10：所有角度都可求.

生15：连接OB，则S四边形OABC=S△OCB+S△OAB.

师：后面两位同学用到了分割法，大家都很棒，书写的时候还要注意规范性.

设计意图：各层次的学生在开放性问题的提出与解决中得到了思维上的拓展，学生体验数学思想方法的同时也为后续解析几何的学习奠定了基础.

4.勇于超越

问题7：如图4，若直线l2过点C（0，1）并且与直线l1∶相交于点B，与x轴相交于点E（m，0）（m＜0），四边形OABC的面积是则直线l2的关系式怎样？

图4

学生在这一道含参数的函数综合题上感觉到了挑战，但因为前面的讨论，大部分学生很快明了了求点B的坐标这一解题核心.

普遍解法：S△BCD=S△AOD-S四边形OABC，可得B的横坐标是1，将x=1代入直线l1的解析式可得B

生15、生16则运用分割法求得了B点的坐标.

师：大家运用刚刚所学的方法解决了此题，表现得很好！

师：太不简单了，这是运用了高中的“参数”思维进行解题的啊！

同学们纷纷鼓起掌来.

问题8：问题7中m＜0有用吗？如果将其去掉是否可以呢？

这是一个留给学生课后思考的题目.

设计意图：条件变式和逆向思维的问题设计令学生从不同角度对数形结合思想、坐标法进行了运用与体验，学生分析问题、解决问题的能力在问题的不断变化中得到了很好的锻炼.

二、案例反思

教师在复习课教学时如果仅仅局限于知识的梳理与应用，必然难以激发学生的思维与学习激情，因此，教师应着眼于学生思维的放飞进行有意义的复习课教学.

1.创设情境，触动思维放飞

创设情境往往能够有效避免复习教学的枯燥，教师应着眼于学生认知与情感的发展进行情境的创设，将统领复习核心内容的情境引进课堂以暗示学生思维放飞的方向.本课所创设的“龟兔赛跑”及问题2中的“感知信息”都是围绕本课复习核心而创设的，学生在围绕主体知识的探索中展现出了积极放飞的思维.

2.开放问题，思维放飞有空间

开放的数学问题往往能为学生创造出思维任意驰骋的空间，提出问题往往依赖学生从新的角度思考问题所展现出的创新能力与想象能力.学生在问题2、4、6的解决中所提出的问题相当精彩，教师预设的复习重点及未曾预料的“未来知识”都在学生炽热、缤纷的思考中得以展现.不仅如此，条件或结论上的开放与探索也使学生在更加宽阔的思维空间进行了思路的自我酝酿、矫正，元认知监控水平大力提升的同时也令学生的思维更为活跃而有深度.

3.围绕主题，思维放飞有引领

教师在设计复习教学的问题串时应考虑学生的知识基础、经验基础与能力基础，然后设计出紧扣主题并明确指向核心知识的问题以促进学生的思考与探索.设计的问题可以看似无拘无束，但教师在设计问题时一定要注意其核心思想是统一的，紧紧围绕复习的核心内容并令学生的思维在问题探索中肆意驰骋，学生只有在方向明确的思考中才会顺利达成学习目标的实现.本案例的所有设计都是紧紧围绕一次函数的图像与关系式这一核心知识进行的，坐标法、数形结合、转化思想等也都是本课教学目标中所包含的内容.因为案例中所有问题思想性的一致，学生的思维也始终在核心内容的范畴中尽情驰骋，有的放矢的设计令学生在综合、抽象、创新中不断挑战自己的思维能力，很多学生也在切中题眼的问题分析与解决中展现出了灵活的解题能力，学习收获与效率也因为思维的放飞而提升.

放飞学生思维令数学复习课堂充满智慧，教师应极力促进学生思维的驰骋并因此获得复习课堂的丰盈、生动、深刻与多彩.