“一题一课”中考专题复习——“玩转”两个等边三角形

王 燕 王 超

（1.山东省滨州市惠民县李庄镇中学 山东滨州 251712；2.山东省滨州市滨城区第六中学 山东滨州 256600）

中考把关试题往往都是经过充分的打磨、苦心经营而推出的，既承担了必要的选拔区分功能，又传递着教学导向，值得老师们认真思考，在贯通思路、洞察问题结构之后，还可将考题设计成习题课，开发成“一题一课”，引导学生深入思考。本文选取2015年山东滨州一道把关题，简述求解思路之后，给出该题的习题解题教学设计，抛砖引玉，供研讨。

教学目标：

1.复习等边三角形的性质及判定，平行线的性质及判定，全等三角形的判定及性质，相似三角形的性质及判定等知识。

2.能熟练应用性质及判定灵活的解决问题。

3.结合知识点，能形成知识网络，达到能掌握知识间的内涵和外延，提升复习的高度。

教学重点：复习三角形全等、相似的性质和判定及其运用

教学难点：知识网络的形成，提高数学内容的复习水平和复习效率

教学过程：

一、每日一题

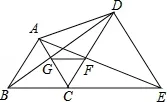
如图，已知B、C、E三点在同一条直线上，△ABC与△DCE都是等边三角形，其中线段BD交AC于点G，线段AE交CD于点F，

求证：（1）△ACE≌△BCD；

生上台讲解解题思路，师适时的点拨。

设计意图：由于等边三角形是特殊的三角形，在多个地方，多次考查与等边三角形有关的题目，以上每日一题是2015年滨州中考题第23题，它就是以等边三角形为载体，考查与其相关的一些几何知识。借此中考题我们深入的探究一下与其相关的内容。

二、问题探究

活动一：作图体验

例 点C是线段AB上的动点（C点不与A、B重合），分别以AC、BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE，AE与CD相交于点M，BD与CE相交于点P.

师：请同学们根据题意，画出图形。

生：在练习本上作图，师板演画图。

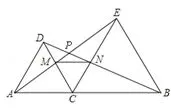
设计意图：为了让同学们在作图过程中，能清晰的观察，体会复杂图形的形成过程，能在复杂图形中分离出基本的图形，容易观察出平行线，相似三角形等，为解决后面的探究问题做好铺垫。

活动二：问题探究，层层递进

探究1.根据已知条件，你能从图中共找出几对全等的三角形？

设计意图：复习等边三角形的性质和全等的判定方法，发散学生思维，类比证明三角形全等的方法，达到融会贯通。

探究2.图中除了已知两个等边三角形的内角是60度，还有哪些角为60度？

设计意图：探究等边三角形，复习等边三角形的判定方法，证明∠DPA=∠EPB=60°，并为后面的斜8字图三角形相似和图形变换——旋转的性质做铺垫。

探究3.图中有几组平行线？

设计意图：结合每日一题一组平行，及画图过程中的平行线总结3组平行线，复习平行线的判定方法。

说明：前三个探究为了说明等角，等线常用的证明方法和作用。

探究4.根据前面得出来的结论，你能找出图中相似的三角形吗？

设计意图：根据平行线判定三角形相似，进而一一复习三角形相似的判定方法，归纳出三角形相似的基本常见模型：“A”字型，“8”字型，“一线三等角”等常见模型的问题。

师：讲解分析，并板书：相似三角形的常见模型

探究5.你能证明MN2=EN·DM吗？

设计意图：三角形相似性质的延续，要想证明等积式，需要先化成比例式，寻找三角形相似，进而承接上面的探究。有助于学生逆向思维的形成，让学生学会综合分析法证明几何问题。

活动三：深入探究 思维升华

探究6.若AB=10，设AC=x，MN=y，那么你能表示出y与x的关系吗？当x为多少时，y有最值？

设计意图：三角形相似的性质对应边成比例，可得出线段的等量关系，因此可构建关系式，

若是存在两个变量，则可以构建函数解析式，进而解决问题。由此也实现的代数与几何的链接，将几何问题升华为函数问题。

追问：探究6若改成下面的问题，解答和上面的探究6有区别吗？

变式：若AB=10，当点C在AB上动时，是否存在一个位置，使得MN的长最大？若存在，求出这个点C的位置，若不存在，请说明理由。

设计意图：变式问法，是为了让学生接触，在没有变量的前提下，需要自己设出变量，自己搭建桥梁，构建出关系式解决问题，需要学生注意变量的取值范围，要求学生有严密的思维。

三、课堂总结

1.学生总结出反思的问题，根据课堂所学，思考并画出知识网络图，老师点拨。

2.学生尝试总结课堂中用到的数学思想方法。

设计意图：老师点拨构建网络，引导学生把零散的知识捆扎，提升复习的高度，点拨学生总结的思想方法，以待遇到此类问题，以相关的思想方法解决这一类问题。进而达到提升中考专题复习的效果。

教后的几点思考：

1.铺垫问题，基础出发，渐次生长

“一题一课”的教学设计，开课阶段一定要平缓起步，坚持从基础出发，让更多的学生参与到初始问题的思考中来，能否更大范围地调动所有学生的思维是这种课型的实施关键.基础问题的设计又要服务于后续问题，即让这些基础题练习之后有助于思考后面渐次生长出来的能力题、提高题、拓展题，这就需要教师设计时充分关注后续问题的生长.

2.增设条件，靠近考题，启发思考

在基础题引导更多学生参与之后，就可陆续增设条件，靠近原来考题渐次增加强化条件，也不宜全盘托出，需要有必要的铺垫，保持基础偏弱学生探究的兴趣和信心。因此在思维障碍点、解题难点处，教师可以通过必要的追问，或让一些优秀学生重复讲解他们是如何突破问题的关键点、难点的，也有助于让更多的学生理解、贯通思路。

3.重视提炼，渗透数学的思想方法.

在复习课教学中，教师要及时引导学生进行提炼，提炼数学知识、思想方法、解题策略，挖掘动态问题中不变的量，同时要渗透各种数学思想方法。通过提炼、渗透，让学生能够从中理解知识点的内涵和外延，从反思过程中汲取经验教训，巩固和扩大解题成果，进一步提升学生思维的深刻性.