火箭助飞式器材舰上发射外弹道特性分析
颜 彬,马赛尔
(上海船舶电子设备研究所,上海 201108)
火箭助飞式器材作为反鱼雷手段之一,目前广泛装备于大中型水面舰艇,根据干扰、诱骗、摧毁的对象,分为火箭助飞式噪声干扰器、火箭助飞式声诱饵、火箭助飞式深水炸弹、火箭助飞式反鱼雷鱼雷等。通过火箭助飞技术,将器材发送到离本舰不同距离的目标水域,实施软硬对抗,形成了多层次、多手段的鱼雷防御体系[1-2],提高了水面舰艇的作战生存能力。
目前,火箭助飞式器材大多由水面舰发射升空,历经空中分离开伞、伞降入水、入水解脱等工作过程,其飞行弹道往往受到发射时刻本舰航行运动、气候条件等因素的影响,造成落点与预设目标点的位置偏差,从而可能影响到预期的对抗效能。因此,有必要对助飞式器材在复杂环境条件下的外弹道特性进行研究,分析各种因素造成的落点偏差,以期为作战系统制定正确的对抗策略提供参考。
1 飞行弹道模型
1.1 火箭助飞段弹道模型
1.1.1 坐标系定义
1)船体运动及气象风场坐标系。
船体在海(水)平面航行,假设为水平面,则船体运动坐标为水平面二维坐标,原点为射击起始点,以航向为轴,向右旋转为射击正弦角(射向为正),反之为负。
气象学上,风向指风吹来的方向。用角度表示风向,是将圆周分成360°,角度按顺时针增加,北风(N)是0°(即360°),东风(E)是90°,南风(S)是180°,西风(W)是270°。其余的风向σ都可以由此计算出来。
图1为船体运动坐标及气象风场坐标,图中,β为射向角,σ为风向角。
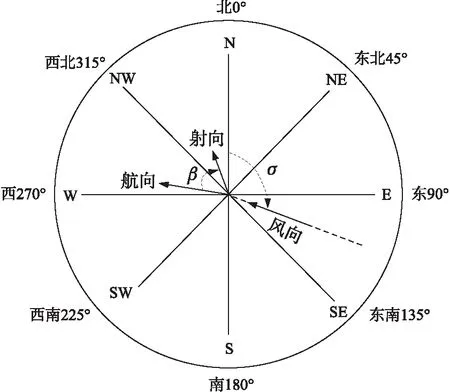
图1 船体运动及气象风场坐标
2)质心运动坐标系。
质心运动采用地面坐标系,如图2所示,其中以发射点O为原点,OX指向正东方,OY指向正北方,OZ轴垂直于水平面指向上方。该坐标系定义符合右手定则,其中,φ为飞行速度矢量v在水平面XOY的投影与OX轴的夹角;θ为飞行速度矢量v与水平面XOY的夹角,即弹道倾角。
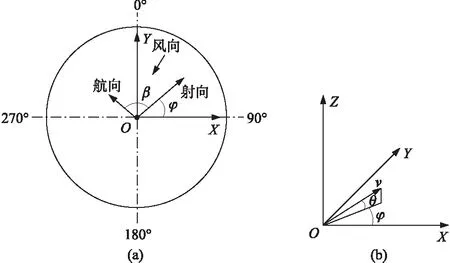
图2 质心运动坐标系
1.1.2 运动方程
对于设计正确的弹箭,飞行中的攻角都很小,围绕质心的转动对质心运动影响不大,因而在研究弹箭质心运动规律时,可以暂时忽略围绕质心转动对质心运动的影响,即认为攻角δ=0。为了使问题简化,做如下基本假设:
①火箭绕弹体轴的转动是无惯性的;
②在整个弹箭运动期间攻角δ=0;
③弹箭的外形和质量分布均关于纵轴对称;
④地表为平面,重力加速度为常值,方向垂直向下;
⑤科氏加速度为0。
考虑到弹道条件和气象条件在非标准条件下对质心运动的影响,需建立非标准条件下的质心运动方程用于实际弹道计算。
火箭运动的弹道条件主要指发射时的初始速度大小和方向,这里特指水面舰艇在发射时刻的航速和航向。由于速度的改变并不影响质心运动方程的组成,故可直接用弹箭运动方程组来求解质心运动。
气象条件主要包括气温T、气压p、空气密度ρ和风速vw。风速vw又可分解为纵风vwx和横风vwy。纵风是平行于射击面的风,顺射时为正;横风是垂直于射击面的风,顺射向看时,从右向左为正。风速改变了弹箭相对于空气的速度,而空气阻力是与相对速度有关的。由相对速度vr=v-vw,可得其在地面坐标系上的分量表达式:
vr=(vx-vwx)i+(vy-vwy)j+vzk
(1)
式中:i,j,k是地面坐标系三轴上的单位矢量;vx,vy,vz是速度矢量v在地面坐标系3个轴上的分量。
考虑到在基本假设下作用于弹箭的力包括火箭发动机推力、空气阻力和重力,同时忽略飞行中除常值风以外的随机干扰对作用在火箭上的法向力的影响,可写出非标准条件下的弹箭质心运动方程:
(1)
式中:C为弹道系数,g为重力加速度,FP为火箭发动机推力,m为弹箭飞行时的质量,qm为火箭发动机工作时燃气从喷管排出的质量流量,mg为推进剂质量,tk为火箭发动机工作结束时间,t为发动机工作时间,m0为弹箭初始质量,G(vr,cs)为阻力函数,cs为空气中声速,H(z)为空气随高度z变化的密度函数。
补充关系式[3]:
(2)
式中:标准气象条件气压p0N=101.333 kPa;地面虚温T0N=288.9 K;干空气气体常数Rd=287.14;标准空气密度ρ0N=1.206 3 kg/m3;空气比热比γ=1.4;Ig为发动机比冲量;Ae为喷管出口面积;i为弹形系数,d为弹径,Cx,0N(Ma)为采用1943年阻力定律的标准弹阻力系数。
(3)
(4)
联立式(1)~式(4),通过四阶龙格库塔法求解微分方程,即可解出火箭飞行弹道参数。
1.2 伞-弹运动模型
考虑到火箭助飞式器材采用的减速伞面积较小,在高速飞行状态下开伞非常迅速(理论情况下开伞时间不到0.1 s)。另外,在伞-弹体轴坐标系下,侧向气动力系数远小于轴向气动力系数。因此做如下假设:①降落伞瞬时开伞,不考虑开伞动态的影响;②在伞-弹体轴系下,不考虑侧向气动力的影响。
计算中涉及到气流坐标系OXqYqZq及伞-弹体轴坐标系OXsYsZs,它们的定义根据传统方法,在此不做赘述。伞-弹系统在地面坐标系下的运动动力学方程可以写成如下形式[4]:
(5)
式中:α为迎角,即气流坐标系的OXq轴在伞-弹系统对称平面OXsZs上的投影与伞-弹系统OZs轴反方向延长线之间的夹角,若OXq轴相对于OYsZs平面而言偏向OXs轴一方,则α为负;ψ为侧滑角,即气流坐标系OXq与伞-弹系统对称平面OXsZs之间的夹角,若OXq轴偏向伞-弹系统对称平面右侧,则ψ为正。FD为减速伞受到的阻力;ms为伞-弹系统总质量,包括自身质量mxt和附加质量mf。
补充关系式[4]:
(6)
式中:CD为伞的阻力系数;A为伞的名义面积;ρ为空气密度;注意α角的换算:当uz>0时,α=αcal-π,αcal为α计算值。
联立式(5)~式(6),由火箭助飞段弹道模型求出分离点的运动参数,并以此作为伞-弹系统运动模型的初始条件,即可求解出分离后伞的运动轨迹。
2 算例分析
初始参数:发射时,舰艇航速7.5 m/s,航向90°,发射舷角β=-120°(即射向角),如图3所示。发射倾角θ0=35°;风场条件:风速10 m/s,风向σ=45°,暂不考虑风速随高度的变化以及垂直方向的风。空中分离设定时间为10.5 s。弹体和降落伞相关参数这里不做详细说明。
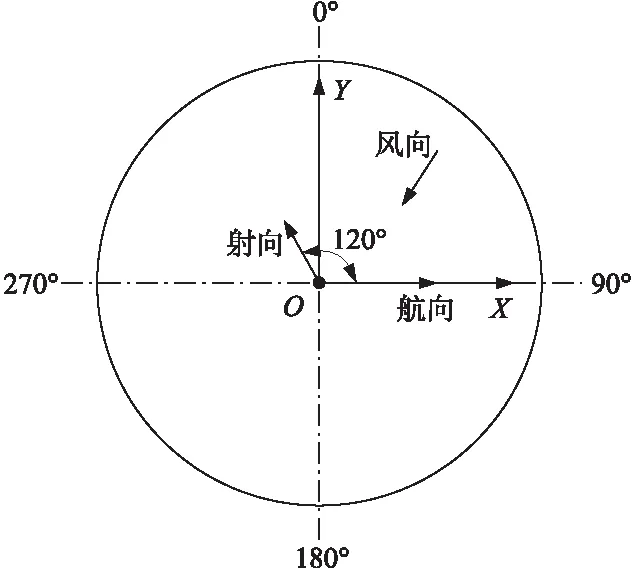
图3 发射初始条件
由航向和发射舷角可得初始侧偏角φ0=120°。由航向和航速可得初始vx0=7.5 m/s,vy0=-13.0 m/s,vz0=-10.5 m/s。由风速和风向可得:vwx=vwy=-7.1 m/s,vwz=0。将以上初始条件作为式(1)的初始值,通过编程计算,得到的计算结果如图4~图6所示。
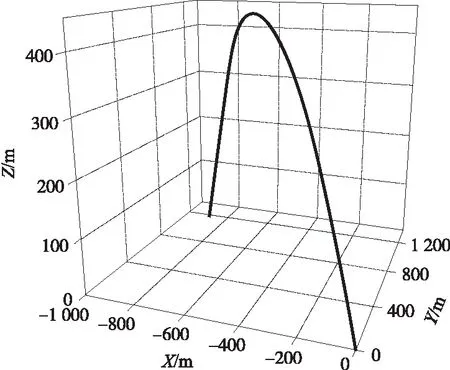
图4 弹体运动三维轨迹
从图4~图6可知,火箭助飞器材从发射至入水经历约28.9 s,落点坐标:X=-893.1 m,Y=1 193.8 m,Z=0。当t=10.5 s时,分离后的弹体在减速伞阻力作用下速度从120.2 m/s快速降至24.8 m/s,弹道倾角从-5.1°快速减小至-49.4°,随后在重力作用下速度略有上升,当重力和阻力达到平衡时,速度稳定在28.3 m/s,最终弹体以-69.3°入水。
为了说明标准条件和非标准条件(即考虑发射平台初始状态和风场条件)下落点的差异,将发射时刻初始速度设为0,且忽略风的影响,其余参数保持不变,对弹道进行了重新计算,图7~图9给出了2种状态的弹道曲线。从图7可知,当舰艇静止发射时,在不考虑风的因素下,弹体落点坐标为(X=-835.6 m,Y=1 447.3 m,Z=0),说明在航速和风速影响下,弹体落点发生了偏移,两点偏移距离达到了259.5 m。显然,若增大航速或风速,将使两点距离继续增大。从图8可知,当器材发射时航速和风速不为0的情况下,其飞行速度尤其是分离前的速度受到明显影响,进而影响到其他弹道参数以及分离时的参数。由图9可知,标准条件下,器材以-90°下降入水(即垂直入水),而非标准条件下的入水角度为-69.3°,说明非标准条件尤其是风速对入水姿态影响较明显。

图7 标准和非标准条件下弹道曲线的比较
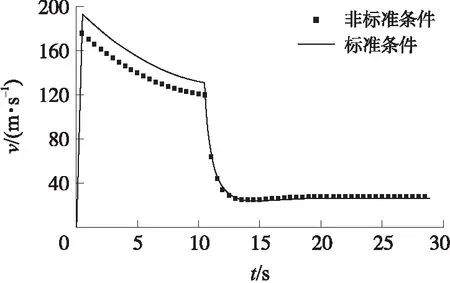
图8 标准和非标准条件下速度变化曲线的比较

图9 标准和非标准条件下弹道倾角变化曲线的比较
3 结论
本文从作战实际使用工况出发,通过建立飞行弹道方程,定义合理的坐标系,分析了火箭助飞式器材在舰上发射时受到本舰航行和海上风场条件影响下的外弹道特性,并将标准和非标准条件下的落点坐标进行了比较,从分析结果来看,火箭助飞式器材空中飞行弹道受本舰航行速度和风的影响较明显,当达到一定的条件时,很有可能造成落点偏差超出预期值,进而影响到作战效能,因此,在制定作战策略时必须综合考虑外部条件的影响,通过弹道修正方法[5],尽可能降低外在因素对弹道的消极影响,提高落点精度。

