再生式液体发射药火炮喷嘴内空化流动研究
孙明亮,刘 宁,张相炎,陆 林
(南京理工大学 机械工程学院,江苏 南京 210094)
再生式液体发射药火炮(regenerative liquid propellant gun,RLPG)是一种新概念火炮,其主要结构形式如图1所示。RLPG利用再生喷射差动活塞将液体发射药高速喷入燃烧室内雾化燃烧,推动弹丸运动,通过控制液体发射药的喷射规律,在不增大火炮最大膛压的前提下提高火炮威力。大量试验研究表明,液体在喷嘴内部的高速流动会伴有空化现象的发生,生成的蒸汽会影响液体的流动特性。液体发射药火炮喷嘴内部的流动现象作为上游边界条件会影响内弹道喷射起始阶段射流破碎[1-2],进而影响到后续雾化燃烧[3-4],对RLPG内弹道再生喷射循环的进行有重要影响。
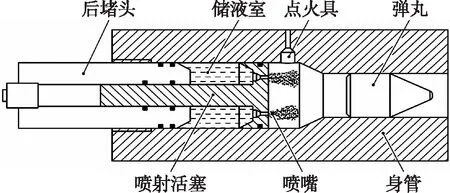
图1 再生式液体发射药火炮结构示意图
对于喷嘴中的空化现象,国内外学者很早就开始了研究。目前对于空化的研究主要集中在内燃机上,试验研究和数值模拟研究是2种主要手段。文献[5]使用激光带研究加大20倍的透明柴油喷嘴中的空化现象,得到了空化流动的3种典型的状态,即单相流动、空穴流动和水力倒流。在高压喷射情况下,喷嘴中的高速流动很难通过试验观察得到详细数据,计算流体力学(computational fluid dynamics,CFD)方法已经成为研究喷嘴内部空化流动的一个重要技术手段。文献[6-11]基于CFD方法建立了喷嘴内部多相流模型和空化模型,为后续研究奠定了基础;张军等基于标准k-ε湍流模型模拟了2种不同结构的柴油喷孔中的流动及空化现象[12];文献[13]通过数值模拟方法研究了内燃机喷嘴内部的空化及其对喷雾的影响;谢阳等通过单气泡溃灭模型和标准k-ε湍流模型模拟了二维喷嘴中的空化现象[14],并对比X射线成像技术的观测结果,证明使用数值仿真方法研究喷嘴空化问题可以和实验结果较好地吻合。但对于RLPG喷嘴内部的空化流动现象,国内外尚未开展研究,也没有研究人员从提高破碎雾化性能角度考虑RLPG喷嘴的结构设计。
为了更加深入研究RLPG内弹道过程,本文采用CFD方法并结合RLPG喷嘴工作特性,分析再生喷射差动活塞喷嘴内部液体发射药的流动现象,研究喷嘴结构形式、内部倾角和喷射压力对空化流动的影响规律,计算空化流动情况下的喷嘴出流状态,为进一步研究液体发射药射流在燃烧室内的破碎、雾化、蒸发和燃烧过程提供上游边界条件。
1 计算模型及验证
1.1 多相流模型
多相流模型采用Euler模型,该模型中各相具有独立的连续性方程和动量方程,气液两相既可以相互掺混也可以互相独立,对于空化流动和水力倒流均有很好的适应性,更适用于研究RLPG喷嘴中的空化流动现象。控制方程如下。
①第q相连续性方程。
(1)
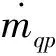
②第q相动量方程。
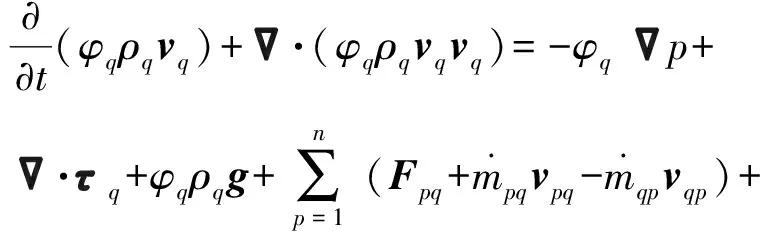
(2)
式中:g为重力加速度;Fq为外部体积力;Flift,q为升力;Fvm,q为虚拟质量力;Fpq为相之间相互作用力;p为流场压力;vpq为滑移速度;τq为第q相的应力-应变张量,表达式为
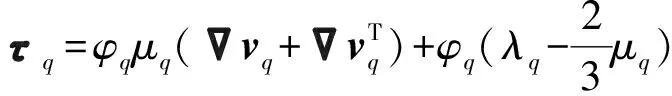
(3)
式中:μq,λq分别为第q相的剪切黏性系数和体积黏性系数,I为单位张量。
1.2 湍流模型
在空化现象的仿真中,近壁面流动的处理对模拟初生空化及空穴发展影响较大,因为空化喷嘴入口附近壁面容易形成回流区。因此湍流模型中的更加精确的近壁面流动处理方法能够显著提升空化仿真的正确性。本次计算中湍流模型采用RNGk-ε双方程模型[15],该模型在标准的k-ε双方程模型基础上进行了改进,考虑了应变率的影响,更加适用于模拟空化现象[16]。湍动能k和湍动能耗散率ε控制方程为
(4)
(5)
式中:Gk为湍动能k的产生项;μeff为有效黏性系数;各常数取值C1ε=1.42,C2ε=1.68,αk=αε=1.39。
1.3 相变模型
忽略热传输和非平衡相变效应,空化流中气相体积分数的输运方程为
(6)
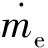
(7)
式中:ρl为液相密度;Ce为蒸发速率常数,取值50;Cc为凝结速率常数,取值0.001;φnuc为液体气核体积分数,取5×10-4;RB为气核半径,取10-6m。
1.4 计算模型验证
采用文献[18]中所用的准二维透明平面单孔柴油喷嘴几何模型对数值计算模型进行验证。使用同样的计算网格、边界条件和物性参数,保持计算中多相流控制方程与空化模型不变,对比标准k-ε湍流模型和RNGk-ε湍流模型的计算结果。喷嘴局部计算域与网格如图2所示,喷嘴流道入口高度h1=0.301 mm,出口高度h2=0.284 mm,流向收缩度为5%,长度L=1.00 mm。采用二维模型划分网格,在喷嘴入口截面两侧和喷嘴壁面同时加密网格。使用文献[18]中所用边界条件,左侧为压力入口,入口压力pi=10 MPa;右侧为压力出口,出口压力po由10 MPa逐渐减小。分别计算不同出口压力po时使用RNGk-ε湍流模型仿真得到的出口质量流量qm,R
和使用k-ε湍流模型仿真得到的出口质量流量qm,S,并与试验测得的流量qm,E进行对比,结果如表1所示,表中,δ为仿真值与试验值的相对误差。
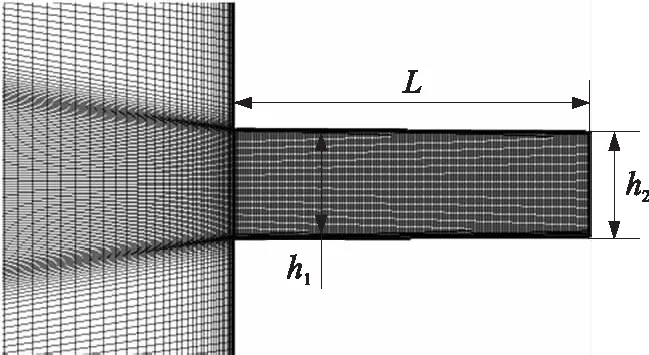
图2 喷嘴局部计算域及网格
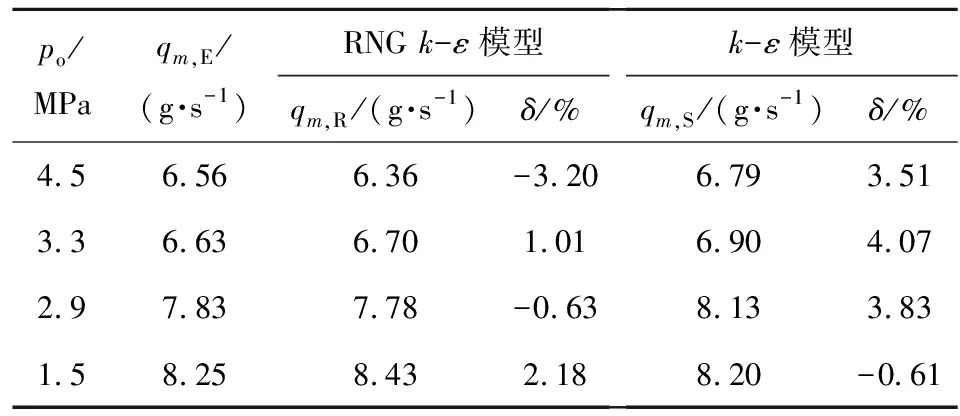
表1 试验流量与仿真流量的对比
使用2种湍流模型求解空化流动问题中的质量流量,误差均小于5%,在工程实践中都是可以采用的。RNGk-ε湍流模型质量流量误差相对零波动,平均误差为-0.16%;k-ε湍流模型计算得到的质量流量普遍大于试验数据,平均误差2.7%。造成这种现象的主要原因是:k-ε湍流模型使用用户提供的常数计算湍流Pr数,计算精度依赖用户对于常数的设置;RNG理论提供了一个计算湍流Pr数的解析公式,计算空化流动适应性更强。
图3~图5分别为试验、RNGk-ε湍流模型与k-ε湍流模型在出口压力po=4.0 MPa,3.0 MPa,2.5 MPa条件下的液相体积分数φl云图。由于RNGk-ε湍流模型使用了多种方法提升计算精度,并提供了一个低雷诺数流动黏性的解析公式,在空化仿真中可以更加准确地预测喷嘴内的低压区和回流区,捕捉到的空穴尺寸也更加准确。
综上,研究空化流动现象的过程中RNGk-ε湍流模型比k-ε湍流模型适应性更强且精度更高。

图3 试验条件下液相体积分数云图

图4 RNG k-ε湍流模型模拟液相体积分数云图

图5 k-ε湍流模型模拟液相体积分数云图
2 数值计算与结果分析
2.1 网格划分与参数设置
如图6所示,本文的主要研究对象分别为RLPG常用的圆柱形喷嘴和圆锥形喷嘴,喷嘴总长30 mm,出口直径4 mm。网格无关性检查发现,RNGk-ε湍流模型对于边界层网格尺寸不敏感,但加密喷嘴入口附近的网格有利于捕捉到更加精确的空化起始位置。本次研究使用二维轴对称模型,在喷嘴入口截面位置同时加密轴向网格与壁面网格,网格总数为85万。将HAN基发射药LP1845及其蒸汽作为纯物质计算,表2列出了计算所需要的主要物性参数[19-20],表中,ρ为材料密度,μ为动力黏度,σ为表面张力,pv为饱和蒸气压。
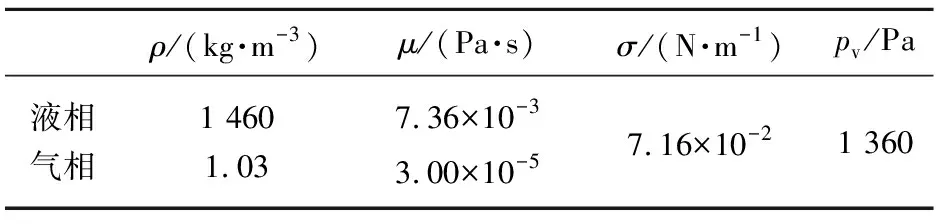
表2 LP1845及其蒸汽主要物性参数
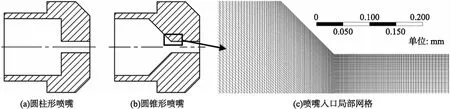
图6 喷嘴结构模型及喷嘴入口局部网格
2.2 喷嘴结构形式对流动状态的影响
首先计算2种不同结构形式的喷嘴内部流动状态。入口压力为30 MPa,出口压力为1.01×105Pa,主要模拟喷射起始阶段喷嘴内部流动状态。2种喷嘴内部液相所占体积分数如图7所示,其内部均发生空化现象,圆柱形喷嘴中空穴尺寸较大,圆锥形喷嘴内部的空化程度较弱。
图8为2种不同结构喷嘴内部的速度矢量图。由于喷嘴结构形式不同,喷嘴内部流体速度矢量差异较大。其中,圆柱形喷嘴内部存在明显的分离流动,喷嘴收口处流动方向与轴线偏差大,喷嘴壁面附近液相流动速度低;圆锥形喷嘴中分离流动强度弱,流动速度相对均匀。这说明喷嘴内部分离流动的强度是影响空化程度的主要因素。
圆柱形喷嘴与圆锥形喷嘴壁面沿轴向气相体积分数的对比如图9所示。在圆柱形喷嘴中距离上游入口0.020 m处发生截面突变,液体经过突变截面以后立刻产生强烈的空化现象,0.020~0.023 m处气相体积分数接近1,说明这一段的喷嘴壁面区域已经完全为气相占据,形成稳定的空穴。空穴会占据流道阻碍液体流动,使轴线处液相流动速度增加,增强射流在燃烧室内的贯穿能力,减弱雾化效果。圆锥形喷嘴中截面变化较为平缓,壁面处最大气相体积分数为0.77,气相与液相始终处于掺混状态,没有形成稳定的空穴占据流道。

图7 起始喷射阶段喷嘴内液相体积分数云图

图8 起始喷射阶段喷嘴内速度矢量图
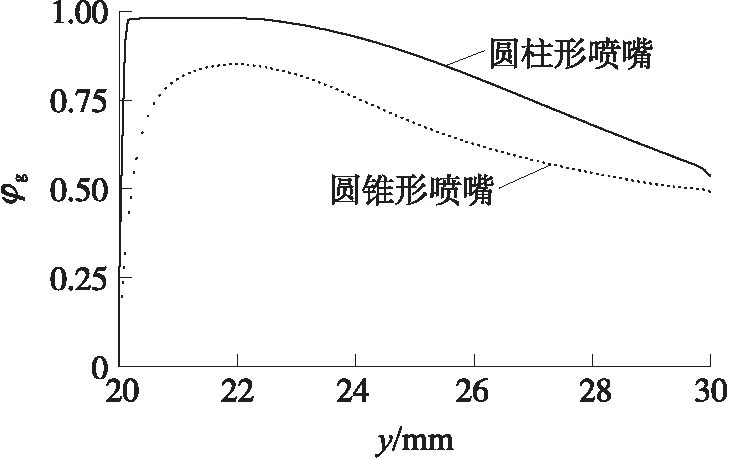
图9 起始喷射阶段喷嘴壁面气相体积分数
综上,2种喷嘴在喷射起始阶段均会发生空化流动现象。圆柱形喷嘴中空化强度大,形成稳定的空穴并占据壁面区域的流道,提高射流轴线上的速度,使射流在燃烧室内的贯穿能力增强,不利于后续雾化燃烧的进行,易诱发不稳定燃烧,难以建立稳定的再生喷射循环;圆锥形喷嘴内部气相与液相互相掺混,提高了射流的起始扰动并破坏了射流表面的完整性,有利于射流在燃烧室的初次破碎,易于形成良好的喷射循环过程。考虑到RLPG的燃烧稳定性,圆锥形喷嘴更有利于提高射流在喷射起始阶段的初次破碎,使后续雾化燃烧顺利进行。
2.3 喷嘴倾角对空化流动的影响
为进一步优化圆锥形喷嘴内部结构尺寸,本节研究喷射起始阶段喷嘴倾角对空化的影响程度。图10为喷嘴内部倾角θ=30°,45°,55°情况下喷嘴内液相体积分数云图。在倾角为30°时,喷嘴内部空化程度较低,空穴贴近壁面,对喷嘴出口的流动状态影响较小;倾角为45°的喷嘴中空穴所占空间增大,气液掺混区域增加,有助于射流的初次破碎;倾角为55°的喷嘴中空化强度进一步增大,气相被液相裹挟向喷嘴出口处发展并与燃烧室内的气相连接,易形成水力倒流,降低射流在燃烧室内的贯穿能力。
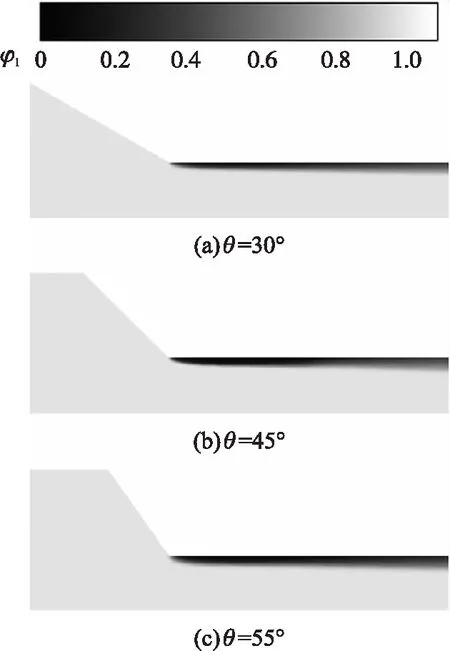
图10 不同喷嘴倾角下液相体积分数云图
图11为喷嘴倾角θ=35°,45°,55°条件下喷嘴出口截面液相速度vl的分布。在35°和45°倾角下气液掺混区未延伸到喷嘴出口,出口处液相流动速度较为均匀;当倾角增大到55°时,喷嘴收口处的气穴阻碍了液相流动,使喷嘴出口处低速区域增加,液相流动受阻,流动速度降低。图12反映了不同喷嘴倾角θ时喷嘴出口的液相质量流量qm,l。随着倾斜角度的加大,空化作用增强,阻碍喷嘴内的流道,使进入燃烧室内的液体质量流量不断减小。
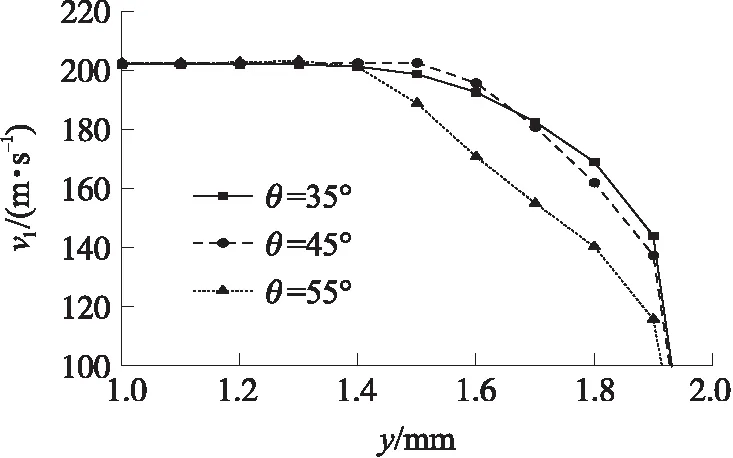
图11 喷嘴出口截面液相速度分布

图12 喷嘴出口截面液相质量流量
综合对比可以发现,过小的喷嘴倾角不利于形成喷射起始阶段的气液掺混;过大的喷嘴倾角会阻碍液相流动进而减小喷嘴的质量流量;35°~45°是相对适中的喷嘴倾角,气液掺混效果较好且可以保证喷射起始阶段液体发射药的质量流量。
2.4 喷射压力对空化流动的影响
在RLPG的内弹道再生喷射循环过程中,喷射压力pi是随着燃烧室压力变化而不断变化的,因此需要计算喷嘴在不同喷射压力pi时的适应性。图13为喷射压力pi=1 MPa,10 MPa,50 MPa,200 MPa时,在45°倾角圆锥形喷嘴壁面上液相体积分数φl沿轴向y变化的曲线。pi=1 MPa时喷嘴内开始出现空穴,由于空化程度较低,空穴在向下游出口发展的过程中逐渐溃灭,并没有形成稳定的空化流动,属于初生空化现象;喷射压力达到10 MPa时,形成的空穴逐渐趋于稳定,喷嘴内的流动状态基本符合空穴流动,气液两相在喷嘴内壁混合并朝喷嘴出口流动;该喷嘴中50 MPa与200 MPa的喷射压力均不会使气相完全占据喷嘴内壁,不会形成水力倒流。图14为喷射压力pi=10 MPa,50 MPa,200 MPa时,在45°倾角圆锥形喷嘴出口截面上液相体积分数φl沿径向r的分布曲线。综合图13与图14中的曲线可以发现,45°倾角圆锥形喷嘴在形成稳定的空化流动后,增加喷射压力会使空化程度加大,但对提高气液掺混区域所占空间影响较小。
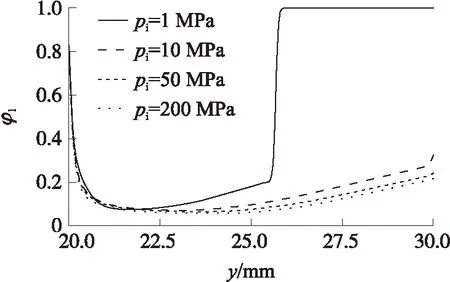
图13 喷嘴壁面区域液相体积分数沿轴向变化曲线

图14 喷嘴出口处液相体积分数沿径向变化曲线
综上,45°倾角圆锥形喷嘴在1 MPa喷射压力时开始出现空化流动现象;喷射压力增加到10 MPa时开始形成稳定的空化流动;进一步增大喷射压力会增强空化程度,但对提高气液掺混区域所占面积贡献不大;即使在200 MPa的喷射压力下,45°倾角圆锥形喷嘴内部依然保持气液掺混,不会出现水力倒流现象。45°倾角圆锥形喷嘴对压力的适应性较好,起始喷射阶段的喷射压力大于10 MPa,即可以获得较好的初始破碎效果。
3 结论
本文通过建立喷嘴内部多相流模型和空化模型,验证2种湍流模型对空化流动仿真的适应性,分析RLPG常用喷嘴内部的流动状态,研究喷嘴入口圆锥倾角和喷射压力对喷嘴内空化流动的影响规律,结论如下:
①在喷嘴空化流动的仿真中,RNGk-ε湍流模型比k-ε湍流模型适应性更强且精度更高。
②在起始喷射阶段,圆柱形喷嘴和圆锥形喷嘴内部均会发生空化流动现象;圆柱形喷嘴内部空化程度较高,不利于射流初次破碎的形成;圆锥形喷嘴内部空化强度适中,有利于建立稳定的再生喷射循环。
③35°~45°是相对适中的喷嘴倾角,喷嘴内部气液掺混效果较好,有利于提高雾化质量。
④45°倾角圆锥形喷嘴对压力的适应性较高;入射压力达到10 MPa,即可形成较为稳定的空化流动;进一步提高喷射压力并不会明显提高喷嘴内部的气液掺混区域所占比例。
研究喷嘴内部的空化流动过程有助于建立更为准确合理的RLPG射流初次破碎模型,也为喷嘴的结构设计提供了理论指导。

