针对高速机动目标的三维非线性微分对策制导律
常晓飞,孙 博,闫 杰,符文星
(西北工业大学 航天学院,陕西 西安 710072)
高超声速飞行器飞行马赫数可达5[1],能够主动持续机动,对现有防御体系构成严重威胁[2]。由于高超声速飞行器红外特征显著,当前多采用红外导引头对其拦截防御。受导引头工作条件等因素的限制,导弹相对于目标不再具备速度优势,故工程上只能采用相对速度高、制导时间短的迎头拦截模式[3],这对导弹机动能力提出了较高要求。临近空间大气稀薄,仅靠气动力无法满足过载需求,必须辅以直接力控制,这使得直接力燃料消耗成为需要考虑的因素。另一方面,随着科技的发展,进攻武器将装有主动探测和拦截告警装置,能够进行主动机动突防[4],使拦截过程构成复杂博弈问题。因此,有必要开展针对高超声速目标的制导律研究设计工作。
微分对策制导律(differential game-based guidance law,DGL)有效结合博弈论的基本思想和最优控制的基本原理[5],将拦截过程视为一类二人零和博弈模型,目标和导弹作为博弈双方,分别使各自的性能指标达到最优,适用于主动机动目标的拦截防御。由于微分对策问题的非线性和复杂性,大量工作集中于数值求法。文献[6]以捕获时间为性能指标,使用梯度直接法寻求鞍点并设计制导律,但模型过于复杂。文献[7]针对弹道导弹拦截问题求解鞍点,但无法拦截主动持续机动目标。非线性模型预测控制(nonlinear model predictive control,NMPC)可以考虑高度非线性系统动力学固有的物理约束和其他苛刻的性能要求,已被广泛应用于航空航天领域的各种制导控制问题[8]。因此,将NMPC和DGL各自优点相结合成为新的研究方向。文献[9]从一类实际的空地追逃问题出发,验证了NMPC实时求解微分对策问题的可行性。文献[10]将梯度迭代法与NMPC结合,设计了二维平面的DGL,但仅针对低速弱机动目标进行分析,无法直接推广到高速机动目标的三维拦截问题。
本文通过分析高超声速目标的拦截模式以及制导律设计需求,在所建立的三维末制导模型基础上,将NMPC和微分对策理论相结合,提出了一种基于NMPC的微分对策制导律(NMPC-DGL)。该制导律以视线角速率和燃料消耗量为性能指标,利用梯度下降法实时求解决策约束型有限时域微分对策(decision-constrained finite-horizon differential game,DCFDG),得到满足精度、过载限制和燃料消耗要求的制导策略,实现对高速机动目标的精确拦截。
1 三维末制导拦截数学模型
1.1 三维弹目相对运动方程
导弹与目标相对运动关系如图1所示。以末制导起始时导弹位置为原点,速度方向为X轴正向,按右手准则建立惯性坐标系OXYZ;MX′Y′Z′为固联在弹体上的与OXYZ平行的坐标系。以弹体为原点,以导弹指向目标的视线方向为r轴正向,按右手准则建立视线坐标系Mrεβ。
图1中,(X,Y,Z)为飞行器在惯性系下的坐标位置,R为导弹与目标的相对距离,qβ和qε分别为视线的偏航角和俯仰角。在Mrεβ坐标系下,假设导弹和目标的加速度及其在3个坐标轴的投影分别为aM=(aMraMεaMβ)T和aT=(aTraTεaTβ)T,则弹目相对加速度为[11]
(1)
考虑自动驾驶仪一阶动态响应:
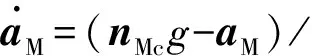
(2)
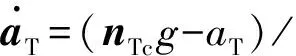
(3)
式中:nMc,nTc分别为导弹和目标的过载指令;g为重力加速度常数;τM,τT分别为双方自动驾驶仪时间常数,并假设对于每个飞行器各通道时间常数相同。
1.2 末制导拦截问题状态方程
(4)
(5)
(6)
从而得到三维空间制导模型的状态变量和输入量:
x=(vrωεωβaMεaMβaTεaTβ)T
(7)
nMc=(nMεcnMβc)T∈NMc
(8)
nTc=(nTεcnTβc)T∈NTc
(9)
式中:NMc,NTc分别为nMc,nTc的定义域。
2 NMPC微分对策制导律
受热防护和超燃冲压发动机工作条件等限制,高超声速飞行器的机动能力有限,但其机动时刻、机动模式不能预测。而DGL不需要对目标未来的机动做任何假设,仅考虑目标的机动能力[12],在性能指标J要求下考虑最坏的情况求取鞍点,并以之为控制策略,使目标机动的潜在作用达到最小。
针对1.2节建立的拦截过程的系统状态方程,基于离散序列,博弈双方分别采用NMPC实时求解DCFDG得到鞍点,算法流程如图2所示。
在预测时域内,设计零和DCFDG,根据弹目相对运动关系进行模型预测递推,采用梯度下降法寻求双方最优决策,在迭代过程中将对方最优决策加以考虑。在控制时域内,导弹根据最优决策进行机动,在时域内保持不变,完成滚动优化过程。将实际局势引入下一预测时域,构成闭环反馈。需要注意的是,该制导律根本上仍是导弹对J的最优化,同时考虑了目标机动能力可能对拦截过程造成的最坏影响,而不依赖于目标的机动,目标机动方式可以独立。
2.1 决策约束型有限时域微分对策的构造
在导弹结构参数确定的情况下,制导律的性能将完全依赖于性能指标。在一个预测时域内,以视线角速度为终端指标,并考虑直接力燃料消耗和过载平滑变化的要求,可构造如下复合型性能指标:

(10)
式中:函数G为终端约束函数;t0,tf分别为预测时域的初始时间和末端时间;Q1,Q2,γ为相应的权系数。对权系数Q1和Q2,只需考虑主对角线上第2个元素和第3个元素,其余元素可设为0。
nMc和nTc满足如下饱和函数约束:
(11)
式中:下标i为M时代表导弹,为T时代表目标。下标j表示物理量在ε轴或β轴的投影。
在一个预测时域内,导弹期望求得最优决策使得性能指标J最小,目标则与之相反,以完成突防,双方构成零和DCFDG:
(12)
2.2 DCFDG的梯度下降法求解
文献[13]提出了利用梯度下降法求解DCFDG的方法,并证明了此方法的有效性和收敛性,具体步骤如下。
(13)
式中:H为哈密尔顿函数,λ为协态变量。
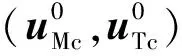
(14)
(15)
(16)
(17)
式中:α1>0,α2>0,是迭代步长;LM,LT是双方的控制约束。
(18)
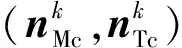
3 仿真校验
为了考核NMPC-DGL的有效性,对导弹迎头拦截高超声速飞行器的末制导段,在目标采用方波机动和博弈突防2种情况下进行数值仿真,并与比例导引律进行对比。
3.1 仿真条件
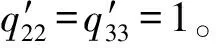
α1=α2=0.618k+0.001
(19)
仿真校验中采用真比例导引(true proportional navigation,TPN):
(20)
式中:η为导引系数,仿真中设为3。
导弹燃料消耗指标为
(21)
式中:ζ为无量纲量;tF为弹目交汇时间;nMj为导弹实际过载;下标j含义与式(11)相同。
3.2 目标方波机动飞行
设目标位置为(30 000,300,300)(单位:m),速度方向与导弹相反,方波机动周期为5 s。表1记录了脱靶量δ、燃料消耗ζ和导弹末端过载大小nMε,F和nMβ,F,结果表明:NMPC-DGL能够在与TPN燃料消耗相当的情况下完成对目标恶劣机动条件下的有效拦截,且具有更小的终端脱靶量。TPN的终端过载达到饱和,而NMPC-DGL终端过载很小,从而保证末端弹道尽可能平直。
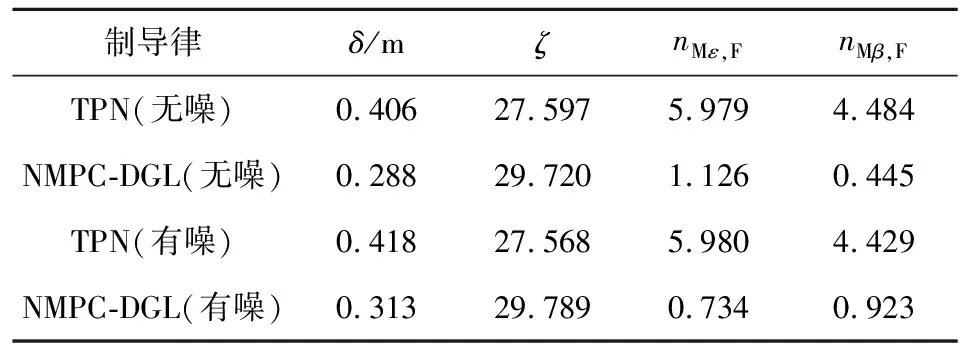
表1 目标方波机动仿真结果
图3给出了在目标做方波机动情况下的导弹三维拦截轨迹。结合图4、图5,在拦截过程中,2种制导律都试图使视线角速度趋于0。与TPN相比,NMPC-DGL在末制导拦截过程前期可以输出较大的过载,使得视线角速度很快收敛。NMPC-DGL对于目标过载有更好的跟踪效果,可以使视线角速度始终保持在0值附近。图3~图5同时给出了含噪声时NMPC-DGL的仿真曲线,可以看出噪声(主要为视线角速度噪声)使过载输出震荡,但飞行轨迹几乎与无噪声时重合。
3.3 目标博弈突防机动
在引入噪声的情况下,假设目标能独立获取与导弹相同类型的制导信息,并采取使J最大的策略机动突防。目标初始位置为(30000,100,100)(单位:m),弹道倾角和偏角分别为3°和5°。表2考察了导弹对目标机动能力存在κ=±50%的预估偏差时NMPC-DGL的仿真结果。TPN脱靶量大于2 m,无法通过直接碰撞对目标进行有效毁伤,而存在预估偏差时NMPC-DGL仍能有效命中目标。
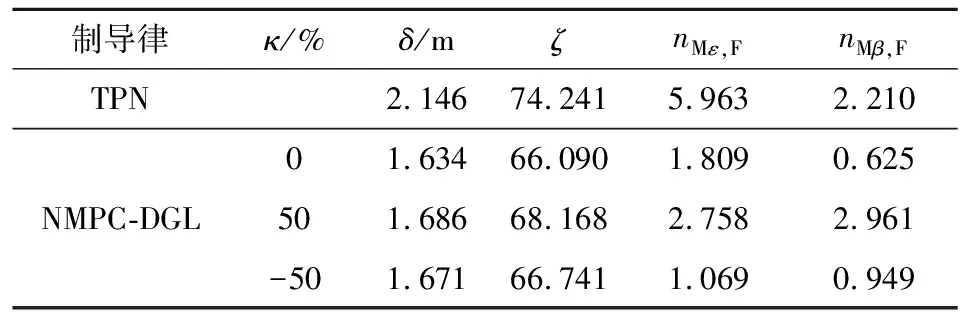
表2 目标博弈突防机动仿真结果
图6~图9给出了目标做博弈突防机动时分别采用2种制导律导引的仿真曲线,其中NMPC-DGL无预估偏差。
图6中的目标轨迹和拦截轨迹都有所差异。结合图7~图9,TPN视线角速度变化缓慢,甚至逐渐增大,使得终端过载饱和。而NMPC-DGL在末制导的中、前期过载较大,能够快速镇定视线角速度。此后目标为躲避拦截,改变过载指令符号,导弹可用过载大,能迅速调整以减小目标机动的影响。但由于超调,双方过载指令频繁变号,引起过载震荡。但过载幅值较小,弹道较TPN更为平直,符合实际工程期望。同时,设计的NMPC-DGL以快速镇定视线角速度为手段来命中目标,并非跟踪目标机动,目标机动能力预估偏差虽干扰了策略求解,但对实际制导结果影响较小。
4 结束语
通过分析高超声速飞行器的拦截模式和制导需求,本文结合NMPC方法,设计了一种微分对策制导律NMPC-DGL。仿真结果表明,NMPC-DGL能够在充分满足动态系统高维非线性、机动能力限制和燃料消耗限制等要求下,实现对目标的精确拦截。与TPN相比,NMPC-DGL能够在保证飞行燃料消耗相当甚至更小的情况下使终端脱靶量更小;且NMPC-DGL克服了比例导引律的主要缺点,末端弹道较为平直;对目标机动能力存在预估偏差时仍能有效拦截,且不需要预估其机动方式。这说明该制导律迎头拦截高速机动目标时具有良好的制导性能。但微分对策理论以最优控制理论为基础,与最优制导律相似,NMPC-DGL对噪声相对敏感,噪声过大会导致制导性能下降,后续工作应结合滤波技术以减小过载输出震荡。

