多层异质复合靶板抗侵彻性能试验及结构优化设计

高 华,熊 超,殷军辉,邓辉咏

(陆军工程大学 石家庄校区火炮工程系,河北 石家庄 050003)

多层异质复合结构结合了多种材料的力学特性,具有质量轻、防护性能好等优点,开展多层异质复合结构抗侵彻性能研究具有重要意义。

陶瓷材料由于具有密度低、硬度高等特点,在装甲防护中得到了广泛应用[1-3],但由于陶瓷材料易脆,限制了其在装甲中的发展和应用。李树涛等[4]利用AUTODYN有限元软件研究金属Al约束SiC陶瓷的复合结构抗侵彻性能,分析了陶瓷约束层厚度对复合结构防护12.7 mm穿甲弹性能的影响,发现对陶瓷进行约束能提升装甲的抗侵彻性能,且各约束层存在最优厚度;郭婷婷等[5]将损伤引入到金属空腔膨胀理论和陶瓷空腔膨胀理论中,忽略靶板侧向边界等因素,研究了陶瓷复合靶抗侵彻性能;赵晓旭等[6]针对新型钢/芳纶纤维复合结构进行优化设计,以最小面密度为目标函数,建立了一定破片质量和撞击速度范围内的结构参数优化模型。对复合靶板进行抗侵彻能力试验、理论分析已成为研究热点[7-10],所得数据虽可对相应复合结构防护性能进行可靠评价,但缺乏体系优化设计方法,难以为多层异质结构系列化合理设计提供有效支撑。

本文进行了2种结构复合靶板抗14.5 mm穿甲弹侵彻试验,分析了复合靶板各层破坏形貌,进行同工况下弹丸侵彻复合靶板数值仿真,在数值仿真模型被验证的基础上,引入配方均匀设计方法,建立相同面密度下复合靶板等效质量防护系数回归模型,研究各层厚度系数对复合靶板防护性能影响规律。利用所建回归模型,针对面密度为9.748 g/cm2的复合靶板进行结构优化与抗侵彻性能试验验证。

1 侵彻试验及结果

1.1 侵彻试验设计

为分析靶板不同结构形式对其防护性能的影响,制定2种试验方案,分别是方案Ⅰ:10 mm氧化铝陶瓷/10 mm芳纶板/6 mm 616装甲钢;方案Ⅱ:10 mm氧化铝陶瓷/6 mm 616装甲钢/10 mm芳纶板。复合结构尺寸长×宽为150 mm×150 mm.依据穿深(depth-of-penetration,DOP)实验方法,每种结构进行3次射击试验,计算其防护系数,参照靶为45 mm 603装甲钢。

试验用枪为14.5 mm弹道枪,枪口到靶板的距离为10 m。试验弹采用56式14.5 mm穿甲弹,弹体简化模型如图1所示。样品在靶架上固定后按预定着弹点垂直靶面入射,射击状态如图2所示,试验靶和后效靶之间无间隙。

图1 试验用弹

图2 靶板夹持状态

首先利用14.5 mm穿甲弹射击603装甲钢,得到穿深Pref;再对复合靶/603装甲钢进行射击试验,得到弹丸在603钢中的穿深Pres,记复合靶穿深为P1,试验穿深示意图如图3所示。最终根据DOP法计算得到复合靶防护系数fm:

(1)

式中:ρ1为复合靶密度,ρref为603钢的密度。

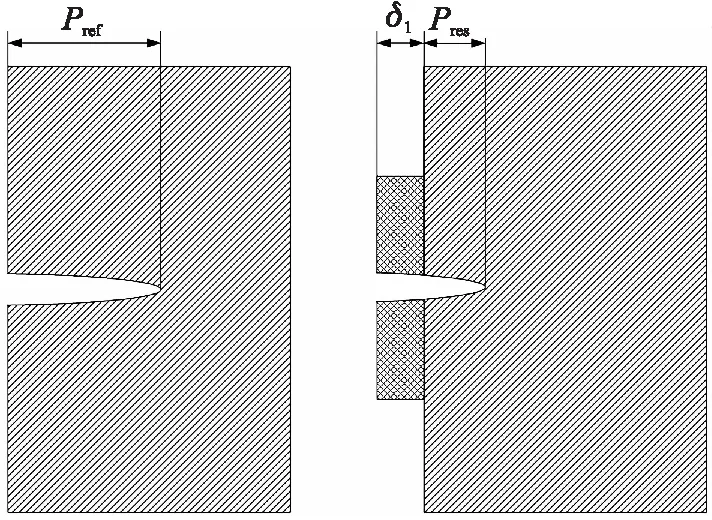
图3 DOP试验示意图

1.2 试验结果及分析

14.5 mm穿甲弹侵彻603装甲钢,穿深Pref为49.7 mm,603钢的密度ρref=7.86 g/cm3,2种结构复合靶均被穿透,即P1=26 mm,试验结果如表1所示,表中,v为弹丸侵彻速度。

由表1可知,弹丸侵彻方案Ⅰ靶板时的平均速度为1 200.9 m/s,603钢平均穿深为6.34 mm,防护系数为3.49;弹丸侵彻方案Ⅱ靶板时的平均速度为1 195.7 m/s,603钢平均穿深为8.14 mm,防护系数为3.37。试验结果说明方案Ⅰ靶板抗侵彻性能高于方案Ⅱ。

表1 靶板侵彻测试结果

图4为陶瓷面板的损伤状态。由图4可见,陶瓷大部分崩落。弹丸侵彻陶瓷板时,在弹靶接触界面产生很大的压力,陶瓷材料晶体由于自身存在微观结构缺陷,在烧结中存在随机分布气孔,弹丸侵彻过程中,缺陷局部位置由于材料微观力学非均匀性,形成局部微裂纹尖端,受拉应力作用,当冲击载荷接近材料破碎强度时,局部微裂纹增多并达到临界值,形成陶瓷破碎。方案Ⅰ陶瓷面板完好程度优于方案Ⅱ的原因在于:弹体较长,导致输入压缩波较长,复合靶相对较薄,因而在弹丸侵彻至陶瓷板后续分层材料时才产生较强反射应力波。芳纶材料波阻抗较低,具有较好的吸波作用,芳纶板位于陶瓷板及装甲钢之间,有效缓解了反射波对陶瓷面板的损伤。

图4 陶瓷板破坏形貌

图5为芳纶材料的损伤状态。由图5可见,2种结构中芳纶板从受冲击面至冲击背面呈喇叭形放大。分析认为:高速弹丸首先对芳纶产生切割破坏并形成瞬时空腔,随弹丸侵彻深入,弹靶接触质点产生速度,并具有运动惯性,使原有弹孔向外扩张,空腔由于惯性发生过度膨胀,直至空腔容积达到最大,从而在芳纶板背面形成喇叭形放大变形锥。方案Ⅰ芳纶产生大量纤维拉伸破坏,有助于充分消耗弹丸动能。

图6为616装甲钢损伤状态。由图6可见,方案Ⅰ中603装甲钢能够为616钢提供支撑作用,提高弹丸侵彻阻力;方案Ⅱ中616装甲钢背板为芳纶,其强度较低,导致弹丸在推动靶板向前运动变形时产生弯矩,在侵彻区形成径向和环向拉伸应力,当达到装甲钢拉伸强度时,在侵彻区产生花瓣状裂纹,降低了弹丸侵彻阻力。

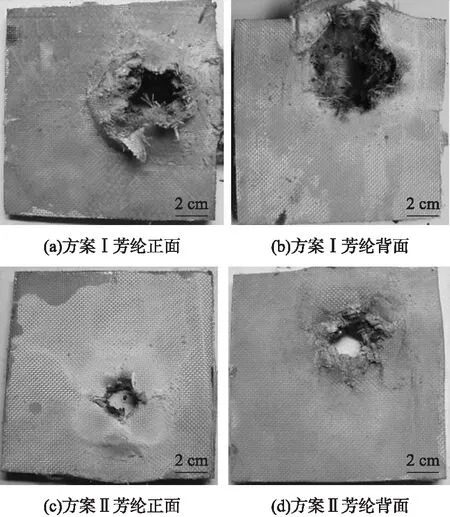
图5 芳纶板破坏形貌

图6 装甲钢破坏形貌

2 数值仿真及优化设计

在侵彻试验基础上开展数值仿真,结合配方均匀设计方法对方案Ⅰ各层材料厚度进行优化设计,实现相同面密度下复合靶板防护性能最优。

2.1 仿真模型验证

利用有限元软件LS-DYNA进行数值分析。由于侵彻模型呈轴对称,因此仅建立1/4模型;弹靶之间采用面面侵蚀接触,各层靶板之间采用自动面面接触;采用8节点Solid164单元划分网格,所建有限元模型如图7所示。

图7 子弹和靶板仿真模型

设定弹丸侵彻方案Ⅰ、方案Ⅱ的初始速度分别为1 200.9 m/s,1 195.7 m/s。弹丸、616钢以及603钢采用Johnson-Cook模型,芳纶采用Solid-Composite-Failure-Solid-Mode模型,陶瓷采用JH-2模型,相关参数参照文献[11-13]。

2种方案的数值仿真结果如图8所示。计算结果表明,方案Ⅰ复合靶板被穿透,并在参照靶产生6.53 mm剩余侵彻穿深,与实际剩余侵彻穿深6.34 mm相比误差为3.0%。方案Ⅱ复合靶板被完全穿透并在参照靶上产生8.86 mm剩余侵彻穿深,与实际剩余侵彻穿深8.14 mm相比误差为8.8%,由此可知,所建有限元模型较为准确。

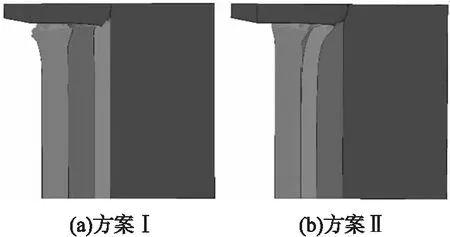
图8 数值仿真结果

2.2 配方均匀设计

在复合靶板面密度9.748 g/cm2(同方案Ⅰ)条件下,利用配方均匀设计及数值仿真结果,得到靶板等效质量防护系数回归模型,进一步求解陶瓷、芳纶和装甲钢厚度最优配比。

约束条件为

3.7d1+1.35d2+7.83d3=9.748

(2)

归一化处理如下:

(3)

式中:d1,d2,d3分别为陶瓷、芳纶和装甲钢的厚度;陶瓷、芳纶和装甲钢的密度分别为3.7 g/cm3,1.35 g/cm3,7.83 g/cm3;D1,D2,D3分别为陶瓷、芳纶和装甲钢的厚度系数。

试验设计采用U15(155)均匀设计表生成,配方及试验结果如表2所示,采用多因素二次回归设计模型,寻找各厚度系数与等效质量防护系数之间的定量关系。根据后退回归分析方法,得到表达式:

(4)

各厚度系数上、下限分别为均匀设计表中对应的最大值和最小值。

表2 各层厚度系数设计及试验结果

为检验回归方程显著性,对回归方程(4)进行方差分析,结果如表3所示,表中,ν为自由度,S2为等效质量防护系数的平方和,F为均方比。

表3 方差分析表

由于F=108.1,而F0.05(4,10)=3.478,故F>F0.05(4,10),说明回归方程在α=0.05水平下显著。

2.3 厚度系数对防护性能的影响

利用回归模型分析厚度变化对等效质量防护系数的影响规律,如图9所示。

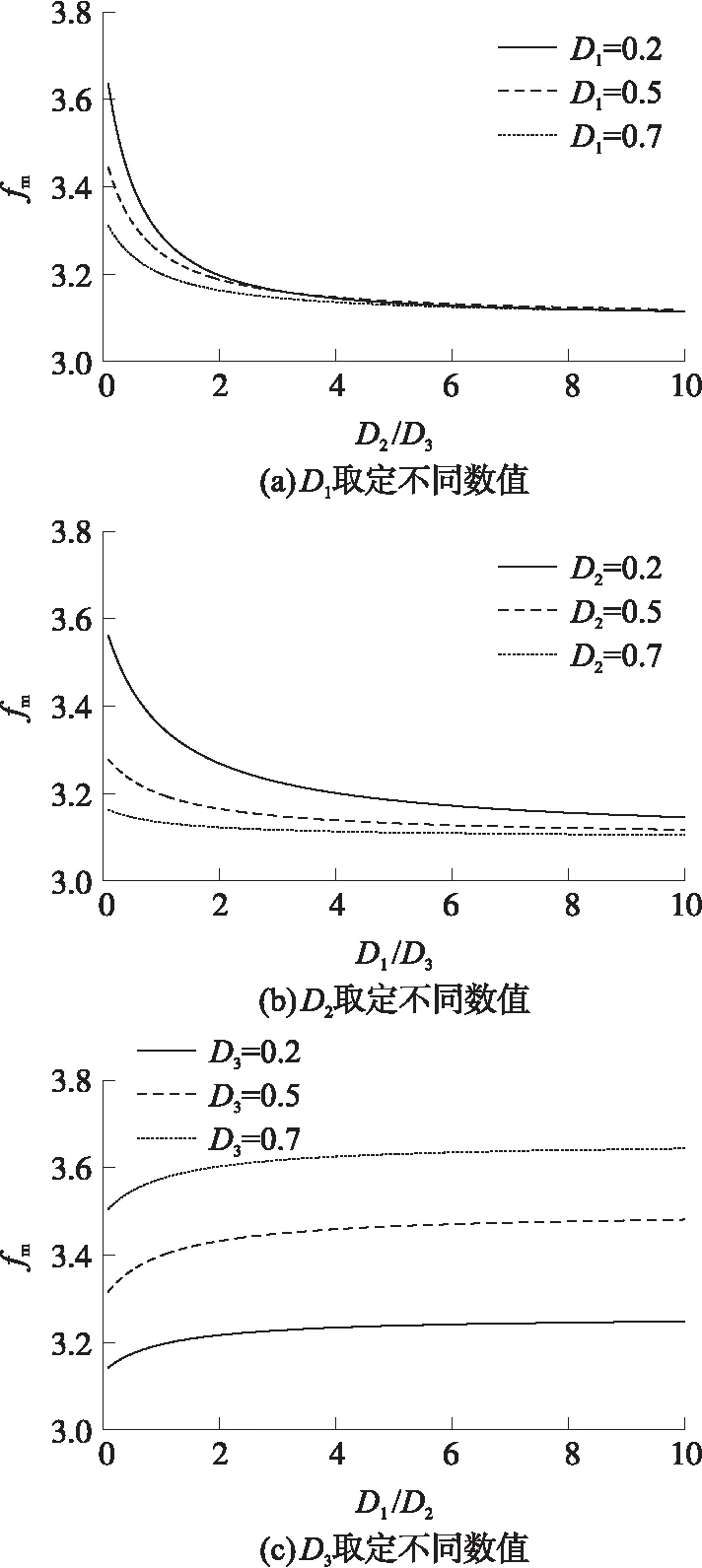
图9 厚度变化对等效质量防护系数的影响

陶瓷厚度系数D1分别为0.2,0.5,0.7,复合靶板等效质量防护系数与D2/D3的变化关系如图9(a)所示,陶瓷厚度系数D1一定时,等效质量防护系数fm随D2/D3增大而减小,最终趋于稳定值。芳纶厚度系数D2分别为0.2,0.5,0.7,复合靶板等效质量防护系数fm与D1/D3的变化关系如图9(b)所示,芳纶厚度系数D2一定时,等效质量防护系数fm随D1/D3增大而减小,最终趋于稳定值,且D1/D3一定,等效质量防护系数随D2减小而增大。装甲钢厚度系数D3分别为0.2,0.5,0.7,复合靶板等效质量防护系数与D1/D2的变化关系如图9(c)所示,装甲钢厚度系数D3一定时,等效质量防护系数fm随D1/D2增加而增加,最终趋于稳定值,且D1/D2一定,等效质量防护系数fm随D3增大而增大。

由此可知,在复合靶板面密度为9.748 g/cm2不变的情况下,存在陶瓷、芳纶和装甲钢最优厚度配比,使得复合靶板等效质量防护系数最高。

2.4 最优配比及试验验证

对回归方程(4)进行规划求解,得到各层最佳厚度系数为:D1=0.247,D2=0.0251,D3=0.728,等效质量防护系数fm=3.67。由式(3)可得:d1=6.5 mm,d2=1.8 mm,d3=9.1 mm,即对于面密度为9.748 g/cm2的复合靶板,防护14.5 mm穿甲弹的最优结构为6.5 mm陶瓷板/1.8 mm芳纶/9.1 mm装甲钢,对应等效质量防护系数fm=3.67。

根据上述分析,对6.5 mm陶瓷板/1.8 mm芳纶/9.1 mm装甲钢复合结构进行抗14.5 mm穿甲弹侵彻试验验证,试验结果如图10所示,弹丸速度为1 203.1 m/s,剩余侵彻穿深为3.98 mm,等效质量防护系数fm=3.68,由此可知优化结果具有可靠性。

图10 验证试验靶体破坏形貌

3 结论

本文通过分析复合靶板结构破坏形貌及数值仿真,结合配方均匀设计对复合结构优化,得出以下结论:

①2种试验方案中,10 mm陶瓷/10 mm芳纶/6 mm 616装甲钢防护性能最优,陶瓷和装甲钢之间加入芳纶有助于缓冲吸能,减小陶瓷损伤面积。

②陶瓷厚度系数D1一定,等效质量防护系数随D2/D3增大而减小。芳纶厚度系数D2一定,等效质量防护系数随D1/D3增大而减小;D1/D3一定,等效质量防护系数随D2减小而增大。装甲钢厚度系数D3一定,等效质量防护系数随D1/D2增大而增大;D1/D2一定,等效质量防护系数随D3增大而增大。

③基于配方均匀设计,建立了面密度为9.748 g/cm2复合靶板等效质量防护系数回归模型,确定最优结构为6.5 mm陶瓷板/1.8 mm芳纶/9.1 mm装甲钢,等效质量防护系数为3.67,试验验证表明优化结果具有可靠性。