浅谈初三物理总复习阶段习题教学有效性的策略

陈娟

摘 要：习题教学是初三物理总复习阶段教学的的重要一环，是学生理解知识、巩固知识、应用知识的基本途径。本文以学生思维需求为出发点，提出了两项习题复习的有效策略：一是运用数学知识构建模型，巧用数学图像培养学生分析解决问题的能力，二是利用变式训练培养学生分析解决问题的能力。

关键词：复习课；习题教学；解题能力；变式训练；教学策略

中图分类号：G633.7 文献标识码：A 文章编号：1992-7711（2018）13-095-2

习题教学是物理教学总复习阶段中不可或缺的重要组成部分。习题是学生理解知识、巩固知识、应用知识的基本途径，是形成技能、发展智力、培养能力的重要手段。教师通过对习题的讲解，可以帮助学生熟练掌握物理知识与技能、训练思维能力、运用物理思想方法。

一、运用数学知识培养学生分析解决问题的能力

在初三物理总复习阶段，教师要注重对各类习题的解题方法的渗透和总结，其中用数学方法对分析解决物理中的难题会起到意想不到的效果，下面结合“物体的运动”这一章的例题进行分析。

1.构建数学行程问题模型——追击与相遇问题在物理机械运动中的应用

很多同学在分析和解决有关相对运动的问题时，觉得非常困难，究其原因是没能巧选参照物，笔者在解决这类问题时巧用小学数学中学过的追击与相遇问题，建构模型，可使问题化繁为简，化难为易。

例1：一个木箱漂浮在河中，随平稳流动的河水向下游漂去，在木箱上游和木箱下游各有一条电动船，两船到木箱距离相同，两船同时驶向木箱，若两船在水中航行的速度如图所示，那么（ ）

A.上游的船先捞到木箱

B.下游的船先捞到木箱

C.两船同时到达木箱处

D.条件不足，无法确定

分析：设上游甲船的速度是v甲，下游乙船的速度是v乙，水流速度为v水，则v箱=v水，

此问题可分解为两个过程，一个过程数学上的追击问题，即上游的甲船与木箱同向而行，甲船去追击木箱，假设追上的时间为t甲，由于两船到木箱距离相同，假设为S，则t甲=S/（v甲-v箱）

另一个过程是数学上的相遇问题，即下游的乙船与木箱相向而行，乙船和木箱相遇，假设相遇的时间为t乙，则t乙=S/（v乙+v箱）

通过比较很容易得出t甲>t乙，故下游的乙船先捞到木箱，本题还可以继续追问：甲要想先捞到船，速度必须满足什么条件？学生很容易列出t甲v乙+2v水

应用1：两艘潜艇相距S，以相同的速度v1成单纵队同向航行，后艇的超声定位器发出信号到达前艇并被反射回来，声音在水里传播的速度等于v2，则后艇发出信号和收到回声两时刻之间的时间间隔为 。

分析：后艇发出声音信号去追击与它相距S的前艇，看做是追击问题，则追击时间为t1=S/（v2-v1），声音由前艇反射回的信号再与后艇相遇，因两艘潜艇保持相同的速度v1同向前进。所以S一定，则相遇时间为t2=S/（v2+v1），总时间为t=t1+t2，代入整理得：t=t1+t2=S/（v2-v1）+S/（v2+v1）。

2.借助数学图像巧编试题——将题目中隐藏的信息利用数学图像展现出来

在物理习题教学中教师要善于挖掘学生做题时错误的根源，利用数学图像巧妙地将易错题进行改编，通过图像勾画出物理情景，与学生错误的认知形成冲突，扭转学生的错误概念，能加深对概念的正确理解。

例2：一物体做变速直线运动，通过前一半路程的速度是6m/s，通过后一半路程的速度是1.5m/s，则它在整个路程中的平均速度为多少？

学生在解答时总是容易出错，究其原因题目中只给出了两个速度值，而路程隐含在题目中，学生就误认为平均速度就是速度的平均值，可见学生对平均速度的概念理解错误。如果我们能够巧妙地把原题巧设情境改编为下面这道题，利用数学图像来解决，学生马上豁然开朗。

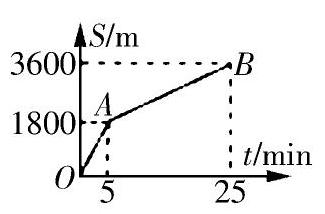
改编题：老师从家中出发到学校后，发现忘带钥匙，于是立刻沿原路返回家中，其中一半路程步行。一半路程骑自行车。路程与时间图象如图所示。

则表示步行的是图中 段，老师骑车的速度为 m/s。全程的平均速度为 m/s。

由于图像上有明确的具体数据，学生很容易算出全程的平均速度，发现全程的平均速度并不等于速度的平均值，学生能及时纠正错误认识，加深印象。同时这样编排的习题不仅容易激发学生学习兴趣，而且指导学生把理论运用于实际，使学生感觉到物理就在身边。

应用2：交通部门常用测速仪检测车速。测速原理是测速仪前后两次发出并接受到被测车反射回的超声波信号，再根据两次信号的时间差，测出车速，第一次从发出到收到经过0.32s，第二次从发出到收到经过0.24s，两次发出的时间间隔为1s，则测到的车速是 m/s。（假设超声波的速度为340米/秒，且保持不变）

由于此题没有任何的图像信息，学生首先必须通过作图来理清整个运动过程，这就需要学生在數学行程问题中储备一定的作图能力，同时学生对“两次发出的时间间隔为1s”理解要清晰才能解出答案。

改编题：交通部门常用测速仪检测车速。测速原理是测速仪前后两次发出并接受到被测车反射回的超声波信号，再根据两次信号的时间差，测出车速，如图甲。某次测速中，测速仪发出与接收超声波的情况如图乙所示，x表示测速仪发出的声波到达被测汽车时，汽车与测速仪之间的距离。从图乙可知，被测汽车前后两次接收到超声波信号的时间间隔是 秒，则该被测车速度是 米/秒（假设超声波的速度为340米/秒，且保持不变）

试题经过改编后，有了甲乙两个图像，把抽象的东西具体化，复杂的问题简单化，只要学生读懂图象蕴含的信息，正确提取有用信息，是解决此类问题的关键。

此外，我们在进行物理数据计算的过程中，也经常用到图像法，如受力分析图、物理过程分析图等，这种方法的运用也十分的普遍。图像法能够使我们的计算的数据更加清晰的表达出来，也能够使我们的计算更加的简单，帮助我们更好的理解物理知识。

二、利用变式训练培养学生分析解决问题的能力

教师在进行习题教学时，经常发现学生对物理概念或公式的适用条件不理解，往往会出现生搬硬套现象，针对这种情况，教师不应急于帮助学生找出出错的原因，而应设计相关类型的题目进行分析比较，形成多变导向，让学生从这一组变式题中领悟公式的适用条件，帮助学生理解相关的物理概念。

例：用如图所示的滑轮组提升重物，货物重300N，动滑轮重为30N，货物上升的速度为0.3m/s，拉力的功率为108W，求：货物被提升时绳端的拉力是多少？该滑轮组的机械效率是多少？货物上升3m过程中，拉力做的功为多少？额外功为多少？

本题在求绳端的拉力，滑轮组的机械效率时，学生对公式F=（G物+G动）/n以及η=G物/（G物+G动）×100%的适用条件不理解，导致解答错误，同样在求额外功时，学生由于对滑轮组额外功的概念理解不透彻，错误地认为克服动滑轮重所做的功即为额外功，为了让学生在易疏忽处、易混淆处加深印象，笔者设计了以下几个变式题。

用如图所示的滑轮组提升重物，货物重300N，在拉力F的作用下，物体以0.3m/s的速度匀速上升。

变式1：若不计摩擦、绳重和动滑轮的重，则拉力F为多少？机械效率为多少？

变式2：若不计摩擦和绳重，动滑轮重30N，则拉力F为多少？机械效率为多少？

变式3：若拉力为120N，则机械效率为多少？

分析与解：（1）若不计摩擦、绳重和动滑轮的重，很明显是一种理想情况，则拉力F=G物/n=300N/3=100N，由于是理想情况，额外功为零，因此机械效率为100%。（2）若不计摩擦和绳重，动滑轮重30N，由于考虑动滑轮的重，我们称这种情况为半理想，则拉力F=（G物+G动）/3=（300N+30N/3）=110N，机械效率为η=W有用/W总×100%=G物h/FS=G物h/Fnh=90.9%。由上面计算可以发现，在没有告诉物体和绳子移动距离的情况下，η=G物/nF×100%，甚至不用知道拉力F，由于不计摩擦和绳重，克服动滑轮重所做的功即为额外功，也可以根据推导机械效率的推导公式η=G物/（G物+G动）×100%计算出机械效率。（3）若拉力为120N，比半理想情况下的拉力110N还要大，所以摩擦和绳重要考虑，应为实际情况，此时额外功包括了克服动滑轮重，克服摩擦和绳重所做的功，则机械效率为

η=W有用/W总×100%=G物h/FS=G物h/Fnh=83.3%。

利用滑轮组提升重物的计算题，方法多，涉及到的计算公式也很多，有些题目看似条件充足，而有些题目又特意设置了多余的条件（即干扰条件）。教师通过变式训练，让学生区分该题是理想、半理想还是实际情况，然后再选择相应的公式进行解题。这样让学生在理解的前提下自觉迁移不同类型的解题方法，而不是简单地套用模仿。

许多题目有很多相似之处，有的题目差别很小，利用变式训练把他们放在一起进行比较，就能让同学们区别他们的不同，遇到新问题容易甄别题目的细节，少犯错误。设计相关类型的变式题进行分析比较，让学生从对比和感悟中概括某一类问题的解题思路，有利于提高学生分析解决问题的能力，同时培养思维品质、创新意识和创新能力，从而達到举一反三、融会贯通的目的。

在复习阶段，有效的习题教学不但有助于加深对物理知识的理解与深化，提高学生解题技巧及分析问题和解决问题的能力，而且也能培养学生创新思维的深刻性、发散性、灵活性、批判性、独创性、全面性、敏捷性等思维品质。

[参考文献]

[1]吕敏.变式教学在高中物理教学中实践一研究.浙江师范大学，2015.

[2]蒋守培.也谈习题变式教学的有效途径.物理教师，2018（02）.