迁移理论在数学教学中的应用初探

文/深圳市龙岗区石芽岭学校 朱志坚

2016年9月， 《中国学生发展核心素养》正式公布，构建了“三个方面、六大素养、十八个基本点”的核心素养体系，旨在培养全面发展的人。我们身为人民教师，在课堂上除了教会学生学习文化知识以外，更重要是让学生学会学习。在各种各样的教学方法中，其中运用认知结构迁移理论进行教学，适当培养学生迁移知识的能力，可尽量做到 “举一反三、触类旁通”的教学效果。

一、认知结构迁移理论

认知结构迁移理论是奥苏贝尔于1963年在有意义言语学习理论的基础上提出，这一理论认为，一切有意义的学习都是在原有认知结构的基础上产生的，不受原有认知结构影响的有意义学习是不存在的。一切有意义的学习必然包括迁移，迁移是以认知结构为中介进行的，先前学习所获得的新经验，通过影响原有认知结构的有关特征影响新学习。认知结构有三个变量：可利用性、可辨别性和稳定性。原有的认知结构就是通过这三个变量对新知识的学习产生影响。

奥苏伯尔还提出，我们老师先设计组织者 （也称 “先行组织者”）。所谓 “组织者”就是在有意义的学习中，在呈现正式的学习材料之前，先用浅显、易懂的语言介绍的一些引导性材料。这些能充当新旧知识 “认知桥梁”作用的材料，称之为 “组织者”。因它呈现在新学习材料之前，故又称之为“先行组织者”。设计 “组织者”的目的，是为新的学习任务提供观念上的固定点，增加新旧知识之间的可利用性和可辨别性，以促进类属性的学习。也就是说，通过呈现"组织者"，给学习者已知的东西与需要知道的东西之间架设一道知识之桥，使他更有效地学习新材料。而且，在认知结构理念中，我们教师是一个组织者，要充分利用好各种材料，改变学生的认知结构变量，提高原有认知结构的可利用性、可辨别性和稳定性，促进新的学习和保持，产生正迁移的作用。

二、数学学科特点

数学是一门研究数量关系和空间形式的科学，它具有严密的符号体系、独特的公式结构、形象的图像语言。它的思想丰富多彩，有转化思想，又有方程思想、数形结合思想、函数思想、整体思想等等。在学生数学能力培养方面，它要求学生应具有基础运算能力、空间想象能力、逻辑思维能力、将实际问题抽象为数学问题的能力等等。但是，在我们的教材体现中，呈现出来的内容只有数学基础知识的概念、定义、定理、公式等，并且课本上的知识相当有限。那又要如何实现培养学生的数学能力和建立数学思想呢？这就要求我们，在平常的教学中，充分利用好认识结构迁移理论，尽量在每一堂课中，培训学生正确而又灵活地使用数学知识解题，产生正迁移，从而掌握好数学基础知识。

三、迁移理论在数学教学中的应用分析

（一）数学概念教学方面的迁移

在数学概念的教学中，我们可以借助以前学过的知识进行迁移。如我们在进行 “乘方”运算概念教学时，可这样操作：把一张纸对折2次，可裁成4张，即2×2张；若对折3次，可裁成8张，即2×2×2张。

问题1：若对折10次可裁成几张？请用一个算式表示 （不用算出结果）。

问题2：若对折100次，算式中有几个2相乘？

学生们可写出：对折10次裁成的张数用以下算式计算：

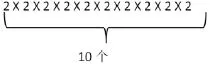
是一个10个2相乘的乘积式。

对折100次裁成的张数，可用算式

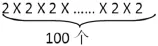
计算，在这个积中有100个2相乘。

问：这么长的算式有简单的记法吗？

回忆我们已经学过的乘法运算概念。我们当时是这样学的：

2个a相加可记为：a+a=a x 2；

3个a相加可记为：a+a+a=a x 3；

4个a相加可记为：a+a+a+a=a x 4；

n个a相加可记为：

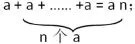
同样，有边长为a的正方形面积可记为：a·a=a2；

棱长为a的正方体体积可记为：a·a·a=a3；

那么，4个a相乘可记为：a·a·a·a=？

n个a相乘可记为：

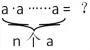
从而可引出乘方这个运算概念：求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂，记作：an。

在这里，我们成功地借鉴了乘法运算的由来：n个相同加数的和的运算，可用乘法表示。类似地，n个相同因数的积的运算呢？学生自然地想到，那它叫做什么运算？怎样表示它显得更简洁？

你看，我们教师只需将它们的相似之处放在一起，让学生进行比较，学生更能从中找到规律，归纳总结经验，轻而易举地得出乘方概念和它的数学表示方法。

讲完乘方的概念后，我们还可顺势而为，分别对乘法运算与乘方运算的异同之处进行比较教学，加深学生对乘方概念的理解。

这样的教学，我们充分应用了认知结构迁移的可利用性和可辨别性，起到 “举一反三，触类旁通”的作用，学生的知识结构生成可更加自然，理解更加深化，记忆更加深刻。

（二）数学公式应用方面的迁移

在数学公式的教学中，我们一定要先教育学生认识其结构特征或其成立的条件，然后才迁移运用到其他领域，灵活解题。

例如：平方差公式的教学中，我们先认识平方差公式： （a+b）（a-b）=a2-b2。其语言表述为：两个数的和与这两个数的差的积等于这两个数的平方差。

其结构特征是：等号左边是两个二项式相乘，且这两个二项式中有一项完全相同，另一项互为相反数，等号右边是乘式中两项的平方差，且是相同项的平方减去相反项的平方。另外，其中字母a、b可以是具体的数，也可以是单项式或多项式。

也就是说，当我们碰到的式子满足平方差公式的左边特征时，我们可直接应用此公式；或满足平方差公式的右边特征时，可逆用此公式。如练习题中的 （-x+2y+3z）（-x-2y+3z），其中相同的项是 （-x+3z），相反的项是2y或-2y，故可直接应用平方差公式得到：（-x+3z）2-（2y）2； 又如， 因式分解a4-b4时，因为a4-b4可化为 （a2）2-（b2）2， 满足平方差公式的右边结构，故可先分解为 （a2+b2）（a2-b2）。

总之，我们教师的教学应充分重视和利用好认知结构迁移，在提高效率的同时，切实提高教学质量。在知识激增和信息革命的今天，知识的迁移更有着它的重大意义，老师应用迁移方法进行教学和培养学生将学到的知识技能成功地迁移到新的情境、新的课题，已经是新时代下的迫不及待的要求。“为迁移而教”是有效教学的一条重要原则， “不需要教”是教学的一项重要目标。老师进行迁移方法教学，有效地培养学生的迁移能力，是教师实现 “教”且为了最终“不教”的关键，是提高学生素质的有效途径。