电流模式Buck-Boost变换器的混沌控制

吴 智，张小平

（湖南科技大学海洋矿产资源探采装备与安全技术国家地方联合工程实验室，湘潭 411201）

采取电流模式控制的Buck-Boost变换器具有易于实现限流、过流保护以及对输入电压具有更快响应速度等优良特性[1]，因而在电力电子领域有着广泛的应用[2]。然而由于该变换器属于变结构强非线性系统，在一定条件下会产生倍周期分岔、边界碰撞分岔、混沌等现象[3-7]，因而直接影响到其运行的稳定性与可靠性。因此研究一种有效的控制方法以抑制分岔与混沌现象，使其能够实现稳定运行具有重要意义。

目前，电流模式Buck-Boost变换器混沌控制方面已开展了一些研究工作[8-11]，并取得了一定的研究成果。其中，文献[8]采用参数微扰OGY（Ott-Grebo⁃gi-Yorke）法可将变换器从混沌态稳定到单周期态，然而该控制方法的控制信号为有源信号且不能随时间连续变化，存在工程实现困难且在噪声环境中易出现阵发失控等问题；文献[9-10]分别提出采用非线性分段二次函数反馈控制法和改善状态关联性控制法对其混沌现象进行控制，然而这两种方法只能将变换器稳定在二倍周期态，导致稳定后电压和电流的纹波相对较高；文献[11]提出一种参数共振微扰法将变换器从混沌态控制到单周期态，但该方法未能给出调整系数的选择依据，只能通过试凑法来确定，因而实用性有限。

针对目前电流模式Buck-Boost变换器在混沌控制方面存在的不足，提出一种改进型指数延迟反馈控制 EDFC（exponential delayed feedback control）方法，取得了较好的效果。文中建立了该变换器的离散迭代映射模型，并对该变换器在上述控制策略下的控制特性进行了分析，得到了实现系统稳定运行时相关调整系数的取值范围，最后通过仿真和实验对上述理论分析的正确性进行了验证。

1 电流模式Buck-Boost变换器改进型ED⁃FC基本原理

下面首先简要介绍电流模式Buck-Boost变换器的基本结构，阐述EDFC的基本原理，并针对其应用到电流模式Buck-Boost变换器混沌控制中存在的问题，提出改进型EDFC方法。

1.1 电流模式Buck-Boost变换器

电流模式Buck-Boost变换器原理如图1所示。其中，Uin为变换器输入电压，S为功率开关管，D为二极管，L为电感，C为电容，R为负载电阻，iL为电感电流，uC为电容电压，Iref为电感参考电流，CLK为时钟信号。该变换器的基本工作原理[12]是电感电流iL与其参考电流Iref经比较器比较后输入触发器的R端，触发器的S端接时钟信号CLK，触发器输出的脉冲信号控制功率开关管的导通和关断，即当时钟脉冲到来时，开关管S导通，电感电流iL线性上升，当iL增加至参考电流Iref时，比较器输出信号复位触发器，开关管S关断，电感电流iL近似呈线性下降，直至下一个时钟脉冲到来时，开关管S再一次导通，从而开始下一个周期的循环。

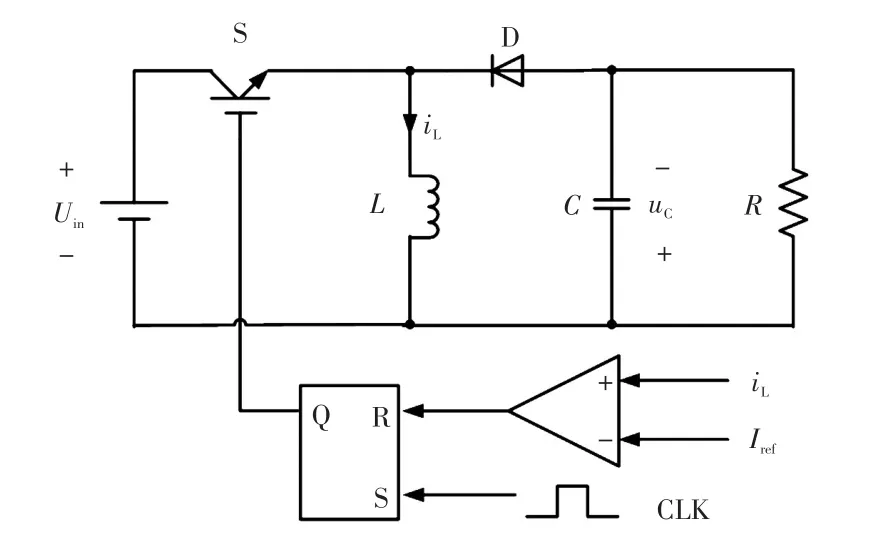
图1 电流模式Buck-Boost变换器原理Fig.1 Schematic of Buck-Boost converter in current mode

1.2 EDFC基本原理

EDFC是延迟反馈控制的进一步发展[13]，其基本工作原理为利用系统输出与自身延迟一定时间的参量之差，以指数函数的形式反馈给混沌系统，进而改变系统的运行状态，实现系统从混沌态到稳定的单周期态的转变。参数反馈控制律可表示为

式中：p0为被控量初值；p为被控量调整值，Δx为反馈调整函数，Δx=exp[y(t)-y(t-τ)]，其中 y(t)为系统输出变量，τ为延迟时间。

将EDFC应用于电流模式Buck-Boost变换器中，其反馈控制率可表示为

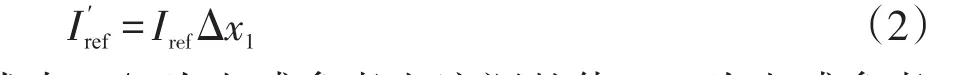
基于EDFC的电流模式Buck-Boost变换器控制系统如图2所示。

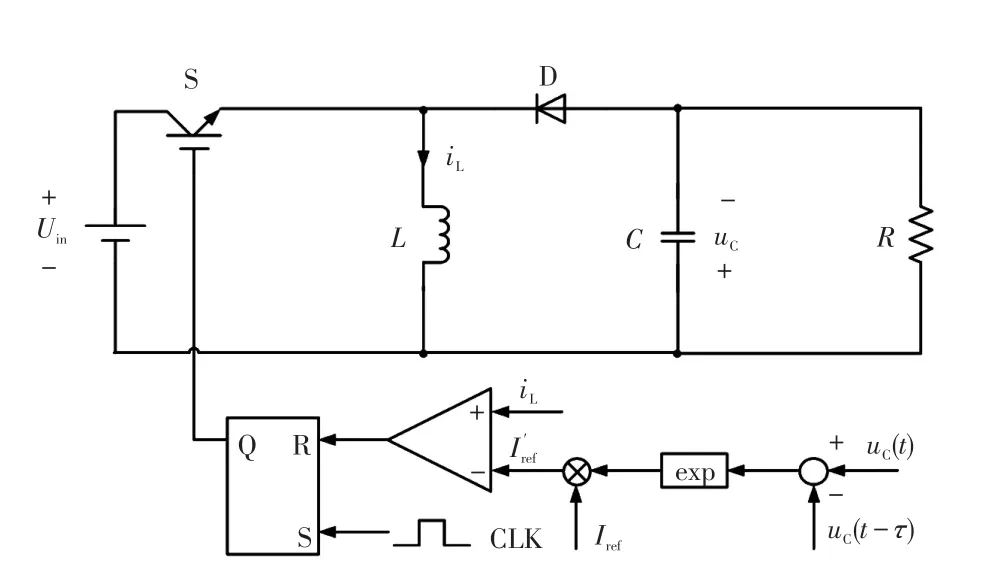
图2 基于EDFC的电流模式Buck-Boost变换器控制系统Fig.2 Control system of Buck-Boost converter in current mode based on EDFC

研究表明，通过在EDFC中加入指数环节，解决了延迟反馈控制无法镇定混沌吸引子中嵌入的高周期不稳定轨道的问题[14]。然而在将EDFC应用于电流模式Buck-Boost变换器的混沌控制时，由于在反馈环节中采用电感参考电流与反馈调整函数相乘的形式来得到电感参考电流调整值，在电感参考电流较大时，存在反馈环节对系统扰动过大的问题。同时该控制方法还因不能对反馈强度进行调节，因而难以达到最佳的控制效果。

1.3 改进型EDFC基本原理

针对将EDFC应用于电流模式Buck-Boost变换器的混沌控制时存在的上述不足，提出一种改进型EDFC方法。该方法通过对EDFC进行改进，有效提高了Buck-Boost变换器混沌控制的效果，其改进具体包括：①将反馈控制律由原反馈调整函数与电感参考电流相乘的方式改为相减，这样可减小对系统的扰动，使得系统更容易趋于稳定；②在反馈调整函数中通过设置调整系数k来调整反馈强度，进而可通过改变调整系数k获得较好的控制效果。

将上述改进型EDFC应用于电流模式Buck-Boost变换器，其反馈控制律为

式中，Δx2=exp{k[uC(t)-uC(t-τ)]}-1，k为调整系数。

基于改进型EDFC的电流模式Buck-Boost变换器控制系统如图3所示。

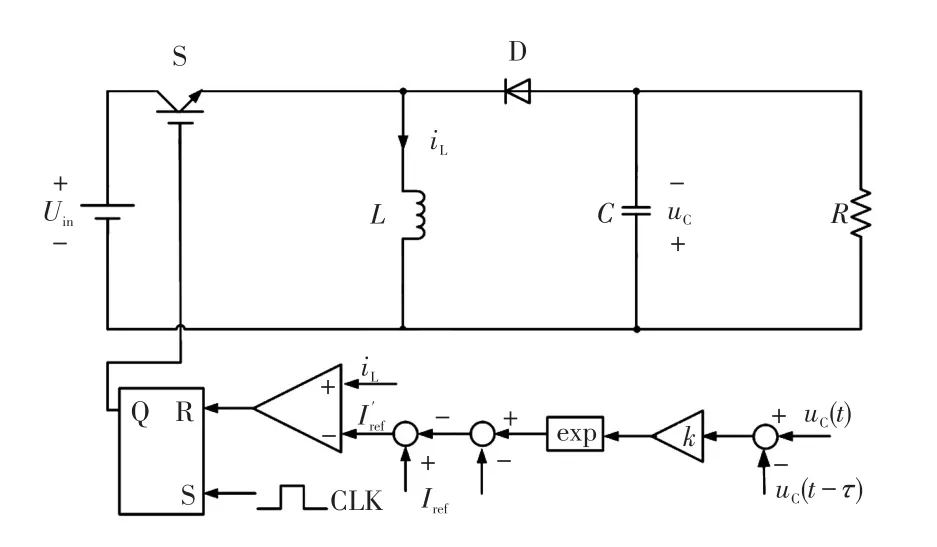
图3 基于改进型EDFC控制的电流模式Buck-Boost变换器控制系统Fig.3 Control system of Buck-Boost converter in current mode based on improved EDFC

要实现上述控制方法，选取合适的延迟时间τ和调整系数k是关键。对于延迟时间τ，通过借鉴文献[15]，将其取为系统开关周期T，这样可保证施加改进型EDFC后，若系统能稳定到单周期轨道，则系统稳定后的单周期稳态解不变；对于调整系数k，可先建立系统的离散迭代映射模型，进而得到系统的雅可比矩阵[16]，通过分析调整系数k与雅可比矩阵特征值之间的关系，获得实现系统稳定运行时调整系数k的具体取值。

2 建立改进型EDFC的电流模式Buck-Boost变换器的离散迭代映射模型

设Buck-Boost变换器工作在连续导电模式，以电感电流iL和电容电压uC为系统状态变量，根据变换器中功率开关处于导通和关断两种状态，并基于基尔霍夫定律建立其状态微分方程，可表示为

对上述状态微分方程式（4）和式（5）求解，并采用频闪映射法将其解离散化[17]，可得

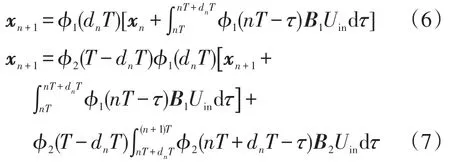
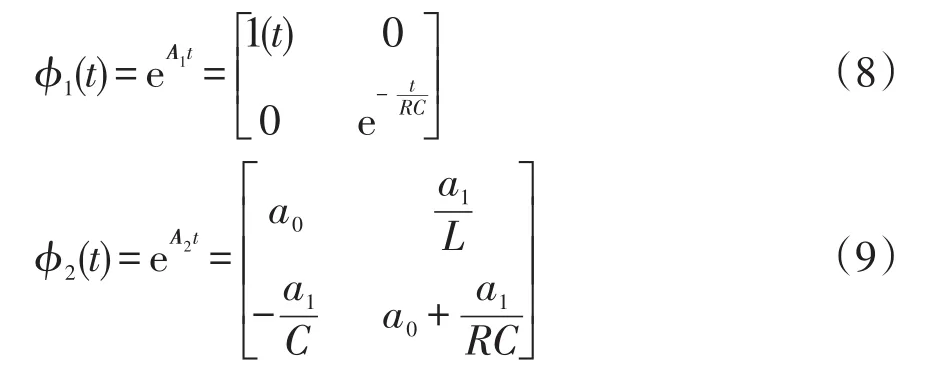
式中：a0=-β-1[α eαtsin(βt)-βeαtcos(βt)] ；a1=- β-1eαtsin(βt)；

再针对电容电压在任意两个连续开关周期的对应时刻进行采样，设其采样值分别为un和un-1，根据该采样值计算得到相应的电感参考电流调整值及电流边界值Ib,n分别为

根据实际电感电流在第n个开关周期的采样值in与其对应边界值Ib,n间的关系，并由状态微分方程的解得到电感电流和电容电压的迭代关系如下。

情况1 若 in＜Ib,n，则变换器中的功率开关在整个开关周期内一直处于导通状态，由式（6）得

情况2 若in≥Ib,n，则变换器中功率开关在开关周期T中的前dnT时间内处于导通状态，在后(1-dn)T时间内处于关断状态，由式（7）得

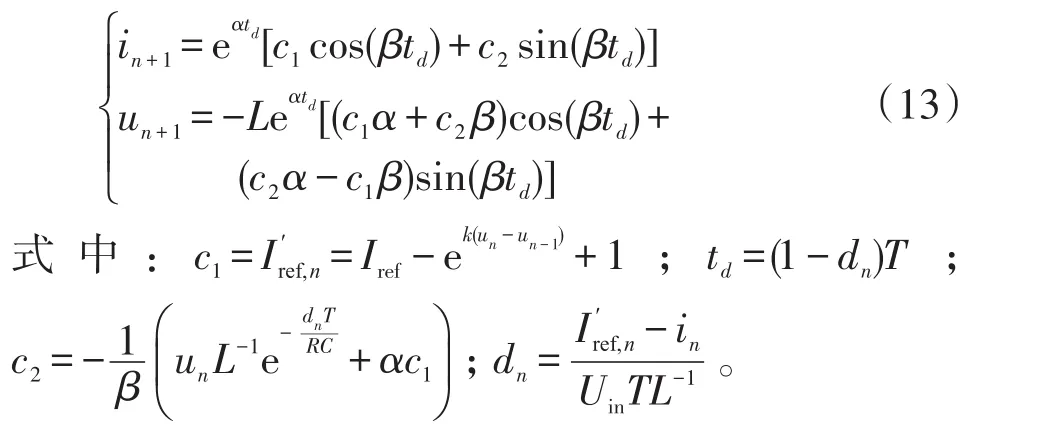
由式（12）和式（13）构成了系统的离散迭代映射模型。

3 电流模式Buck-Boost变换器改进型ED⁃FC混沌控制研究

根据上述离散迭代映射模型，首先简要分析电流模式Buck-Boost变换器的动力学行为，确定其存在的混沌现象；再研究此时变换器在采用改进型EDFC控制后的控制特性，并确定实现变换器稳定运行时其调整系数k的取值范围。

3.1 电流模式Buck-Boost变换器动力学分析

令式（12）和式（13）中调整系数k=0，此时改进型EDFC不起作用，变换器工作于电流模式，基于上述离散迭代映射模型对电流模式Buck-Boost变换器的动力学行为进行分析。选取变换器的相关参数如下：Uin=8 V，R=10 Ω，L=0.3 mH，C=40 μF，T=50 μs，Iref=0～4 A，由此得到系统的分岔图如图4所示。由图4可见，随着电感参考电流Iref从0开始逐渐增加，当Iref=1.8 A时，系统出现倍周期分岔；当Iref=2.3 A时，系统出现四周期分岔；当Iref=2.8 A时，系统完全进入到混沌状态。

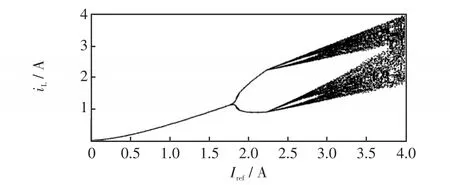
图4 电流模式Buck-Boost变换器以电感参考电流为分岔参数的分岔图Fig.4 Bifurcation diagram of Buck-Boost converter in current mode with inductance reference current as the bifurcation parameter

3.2 基于改进型EDFC的电流模式Buck-Boost变换器控制特性分析

下面首先通过建立Buck-Boost变换器的雅可比矩阵，分析变换器在改进型EDFC下的控制特性及其调整系数k对变换器运行状态的影响，并确定实现变换器稳定运行时调整系数k的取值范围。

若被控系统稳定在单周期态，则in=in+1=IQ，un=un+1=UQ，IQ和UQ分别为系统的不动点[18]。由于变换器工作在连续导电模式时，式（12）不存在不动点，故只需对式（13）的不动点的稳定性进行分析。根据式（13）可得系统的雅可比矩阵为

其中

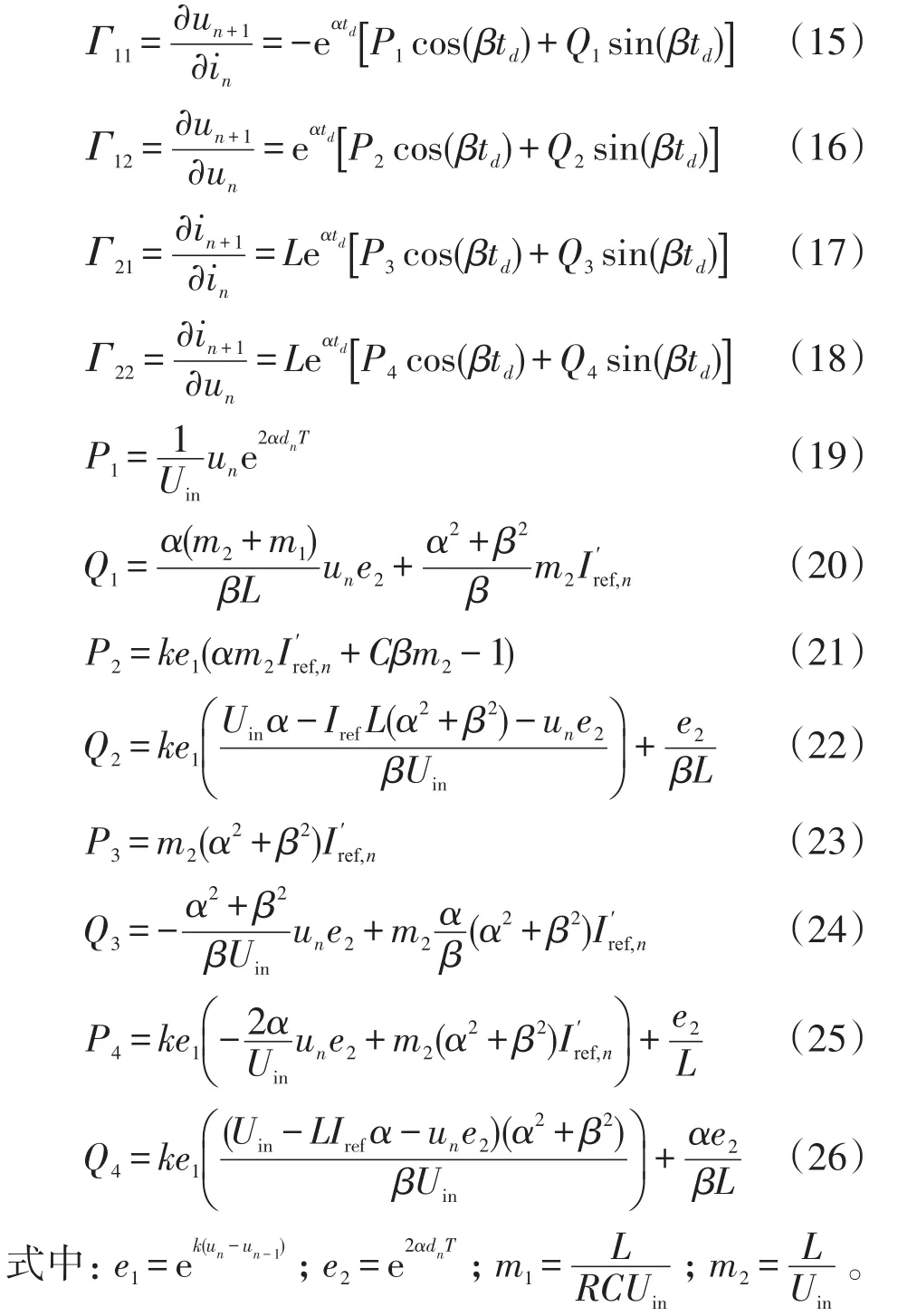
若取λ为雅克比矩阵的特征值，则由式（14）可知，当调整系数k发生变化时，其特征值λ也会发生相应的变化。而根据文献[19]可知，当λ均在单位圆内时，系统是稳定的；当λ中某个特征值为-1时，系统发生倍周期分岔；当λ中某个特征值为1时，系统会生鞍结分岔；而当λ为一对共轭复根穿越单位圆时，则系统发生内玛克分岔。因此，通过分析调整系数k发生变化时对应雅可比矩阵特征值λ的运动轨迹，即可确定实现系统稳定运行时调整系数k的取值范围。

根据第3.1节可知，当Iref＞2.8 A时，变换器处于混沌态，故取Iref=3 A，其他电路参数不变，分析此时变换器在采用改进型EDFC的运行状态。首先将in=in+1=IQ，un=un+1=UQ代入式（13），得系统的不动点为IQ=2.235，UQ=11.277，将上述不动点的取值及变换器主电路参数代入雅可比矩阵J中，得特征值λ随调整系数k变化时的运动轨迹如图5所示。图5中分别用符号“o”和“+”表示两个特征值λ1和λ2，并用箭头表示特征值随调整系数k增加时的变化方向。当k=0.151时，λ1=-1，λ2=0.194 9，此时λ1恰好落在单位圆上，λ2在单位圆内；当k=0.505时，两个特征值均在单位圆上，分别为λ1=0.696 5+0.731 4i，λ2=0.696 5-0.731 4i。可见，只需使调整系数k∈(0.151,0.505)，就可以使系统的特征值均处在单位圆内。而根据文献[19]可知，当系统的特征值全部位于单位圆内时，系统就能稳定，因此电流模式Buck-Boost变换器采取改进型EDFC后，只要令k∈(0.151,0.505)，就可将系统由原来的混沌态控制到稳定态。

图5 特征值λ随调整系数k变化时的运动轨迹Fig.5 Trajectory of the eigenvalue λ varying with the change of adjustment coefficient k

4 仿真研究

为验证上述理论分析的正确性，采用Simulink构建相应的仿真模型进行验证分析[20]，仿真参数如下：输入电压Uin=8 V，电阻R=10 Ω，电感L=0.3 mH，电容C=40 μF，开关周期T=50 μs，电感参考电流Iref=3 A。仿真过程中先对变换器采用电流模式控制，在0.002 s后分别切换至改进型EDFC或者EDFC，设置延迟时间 τ=50 μs，任取调整系数k=0.2，得到电流模式Buck-Boost变换器在采用改进型EDFC前后的电感电流和电容电压仿真波形如图6所示。同样选取延迟时间τ=50 μs，得到EDFC前后仿真波形如图7所示。

由仿真波形可见，采用电流模式控制时，电感电流和电容电压波形均为无固定周期的不规则波形，系统在一定范围内做无规则的振荡，说明此时变换器运行在混沌态；而在切换至改进型EDFC或EDFC后，电感电流和电容电压逐渐从无固定周期的混沌态进入到稳定的周期态，且电流和电压峰峰值明显减小，说明系统被控制到稳定态。同时，对比图6和图7可见，改进型EDFC相对于EDFC来说，前者能将变换器稳定在单周期态，而后者只能稳定在二倍周期态，同时前者稳定速度更快，稳定时的电感电流和电容电压的峰峰值更小，且控制前后不影响变换器原来的频率、电流有效值等参数。由此说明，改进型EDFC获得了比EDFC更好的控制效果。

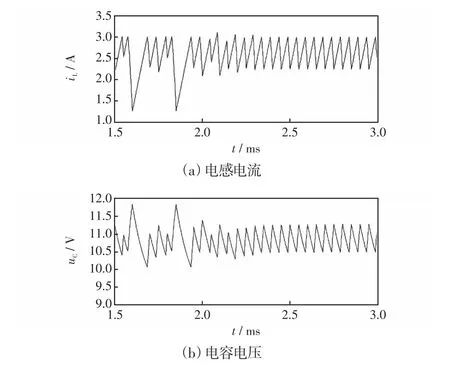
图6 采取改进型EDFC前后的仿真波形Fig.6 Simulation waveforms before and after the utilization of improved EDFC

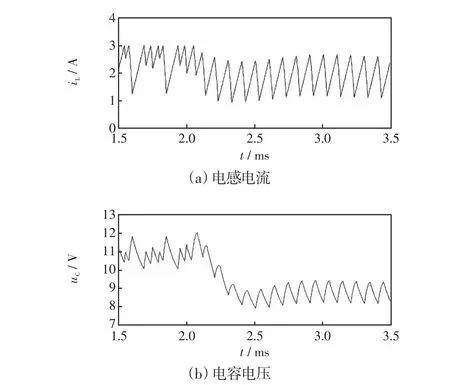
图7 采取EDFC前后的仿真波形Fig.7 Simulation waveforms before and after the utilization of EDFC

5 实验验证

为进一步验证上述理论分析的正确性，根据图2和图3构建相应的实验电路，实验装置如图8所示。实验装置中所采用的电感、电容、电阻参数与仿真时一致，开关管的型号为IRFZ44N，二极管的型号为HER607；采用型号为TMS320F28335的DSP作为系统控制器，并以CASR6-NP电流传感器构建电感电流采样电路，以HCPL-7840光耦隔离放大芯片构建电容电压采样电路；设定输入电压为8 V，电感参考电流取3 A，开关周期为50 μs。

图8 电流模式Buck-Boost变换器混沌控制装置Fig.8 Chaos control device for Buck-Boost converter in current mode

根据上述构建的实验电路，针对电流模式Buck-Boost变换器在分别采用改进型EDFC和ED⁃FC的运行情况进行实验分析，相关控制参数的设置与仿真时完全一致，得到改进型EDFC和EDFC前后的电感电流和电容电压实验波形分别如图9和图10所示。

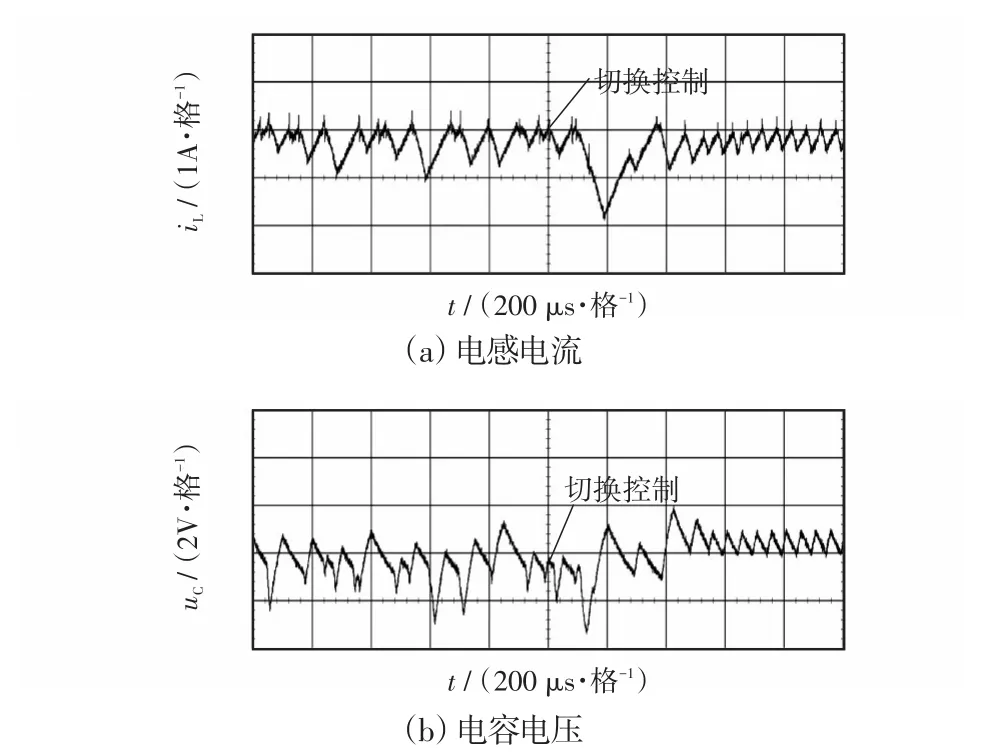
图9 采取改进型EDFC前后的实验波形Fig.9 Experimental waveforms before and after the utilization of improved EDFC

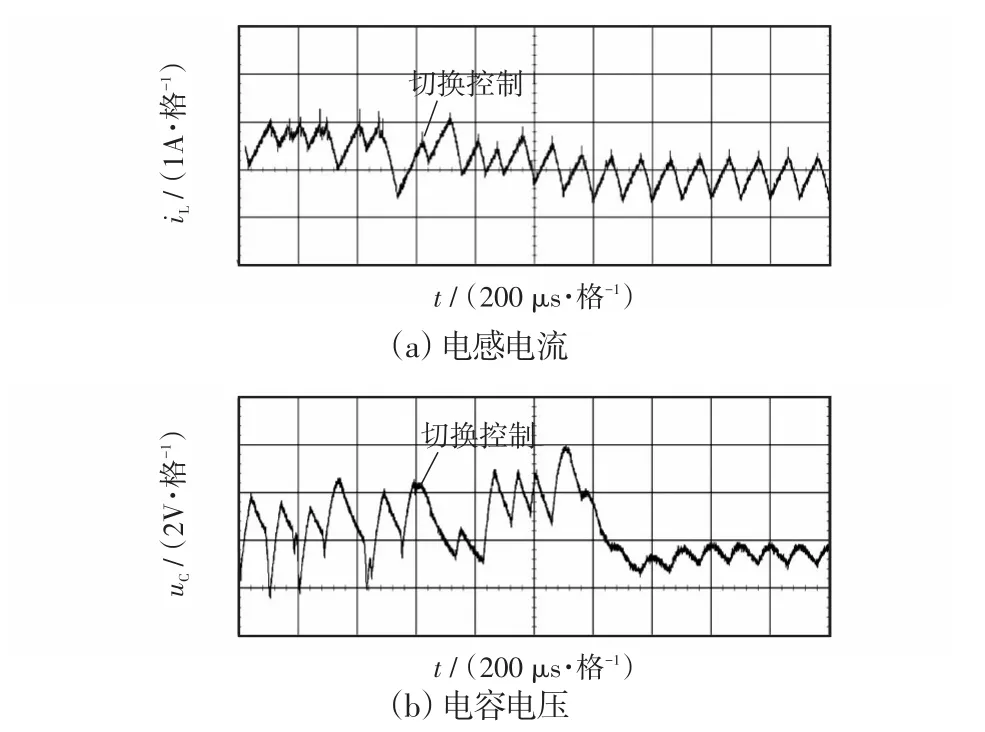
图10 采取EDFC前后的实验波形Fig.10 Experimental waveforms before and after the utilization of EDFC

由实验波形可见，在开始时采用电流模式控制，变换器处于混沌态，而在一段时间后分别切换至改进型EDFC或EDFC，则变换器逐步从混沌态过渡到了稳定态；同时改进型EDFC相对于EDFC来说，其稳定速度更快，稳定后电感电流和电容电压的峰峰值更小，且施加控制后不影响变换器原来的频率、电流有效值等参数。可见实验结果与仿真结果基本吻合，因此进一步验证了改进型EDFC的有效性和可行性。

6 结语

针对电流模式Buck-Boost变换器中存在的分岔与混沌现象，提出一种改进型EDFC方法对其进行控制。阐述了该方法的基本原理，建立了变换器在该方法下的离散迭代映射模型，分析研究了变换器采用该方法后的控制特性并确定了实现系统稳定运行时调整系数的取值范围，最后通过仿真和实验对上述理论分析进行了验证，同时与EDFC进行了对比仿真与实验分析。结果表明，该方法能有效抑制电流模式Buck-Boost变换器中出现的混沌现象，并且相较于EDFC，具有响应速度快，不改变原系统频率、电流有效值等参数，系统稳定后的电流、电压纹波小的优点。