双馈风力发电系统DC-link电压振荡抑制策略

高仕红，毛承雄，王 丹，陆继明

（1.华中科技大学强电磁工程与新技术国家重点实验室，武汉 430074；2.湖北民族学院信息工程学院，恩施 445000）

目前，双馈式感应发电机DFIG（double-fed in⁃duction generator）在变速恒频VSCF（variable speed constant frequency）风力发电系统中已成为主流配置[1-2]。因其特殊的配置和并网方式（部分功率的背靠背变流器拓扑及定子绕组直接与电网相联），导致其对外界扰动非常敏感，如电网电压的扰动，特别是电网电压的突然跌落，将引起DFIG转子绕组的过电流以及DC-link电容的过电压[3-5]。若不采取相应的控制措施，过大的转子振荡电流产生的热量将损坏转子侧变流器RSC（rotor-side converter），而且过高的直流电压将击穿DC-link电容器。在DFIG的转子电路中常配备一套部分功率的背对背变流器结构，为提高DFIG的故障穿越能力，几种改进的控制方法被提出用来控制DFIG的RSC[6-8]，其中如定子磁链去磁法，基于消除定子磁链中的瞬态分量来控制DFIG的转子电流[7]。但在上述控制策略中没有考虑对网侧变流器GSC（grid-side convert⁃er）的协调控制，由于GSC主要用于调节DC-link的电容电压并使其维持相对稳定，因此在一定程度上限制了DFIG的故障穿越能力。

一般正常情况下，对GSC的控制常采用基于电网电压定向的双闭环矢量控制策略，外环为DC-link电压控制环，内环为DFIG转子电流控制环[9]，其控制原理是通过调节内环的转子电流来达到控制DC-link电压的目的。为克服GSC双闭环控制中电压外环响应慢及电流内环对前馈补偿延时的不足，本文提出一种直接控制电容器充电功率的快速GSC单闭环控制策略。通过直接控制DC-link电容器的充电功率，以达到快速抑制DC-link电压的振荡并使其维持相对稳定。本文所提出的GSC控制策略仅有一个功率控制环，同时对外界扰动进行了无延时地前馈补偿。

1 GSC及DFIG的数学模型

配备部分功率背靠背变流器的DFIG典型电路拓扑如图1所示，其中GSC的主要作用是维持DC-link电容电压的相对稳定，以保证DFIG转子回路中的功率能正常双向流动。

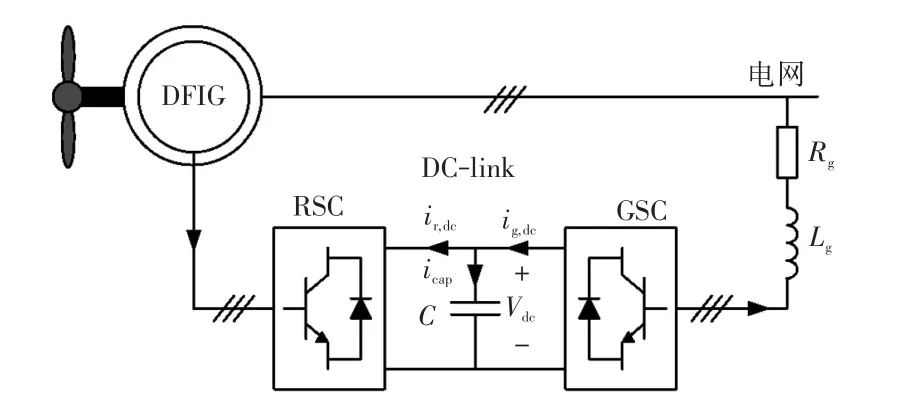
图1 配备部分功率背靠背变流器的DFIG典型电路拓扑Fig.1 Typical circuit topology of DFIG equipped with partial power back-to-back converter

1.1 GSC的数学模型

在同步旋转的dq参考坐标系下，若选择DC-link电压Vdc和GSC交流侧线电流ig,d及ig,q为状态变量，则GSC与DC-link电容器的状态方程为

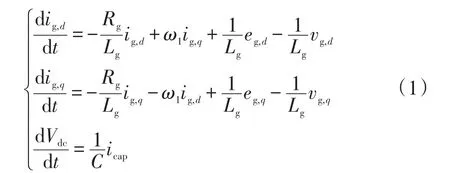
式中：ω1为同步角频率；vg,d、vg,q为网侧变换器交流侧的dq轴电压；ig,d、ig,q为网侧变换器交流侧的dq轴电流；Rg、Lg为网侧滤波电感器的电阻和电感；eg,d、eg,q为电网的dq轴电压；Vdc、icap、C为DC-link电容器的电压、电流及电容。

若GSC采用电网电压矢量定向控制且以单位功率因数运行，则eg,q=0，ig,q=0。结合式（1），忽略GSC的开关损耗，网侧变换器向DC-link提供的功率Pg,dc为

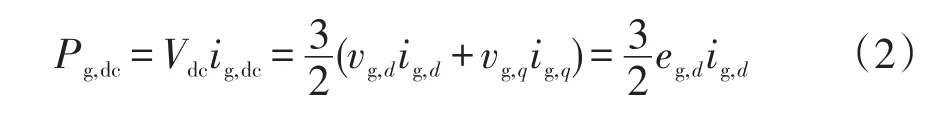
式中，ig,dc为GSC直流侧的电流。

另外，DC-link电容器的充电功率Pdc可表示为

1.2 DFIG的数学模型

同样地，在同步旋转的dq参考坐标系下，选择DFIG的转子电流ir,d、ir,q为状态变量。若RSC采用DFIG定子磁链矢量定向控制，即ψs,q=0，则可得DFIG转子绕组的状态方程为

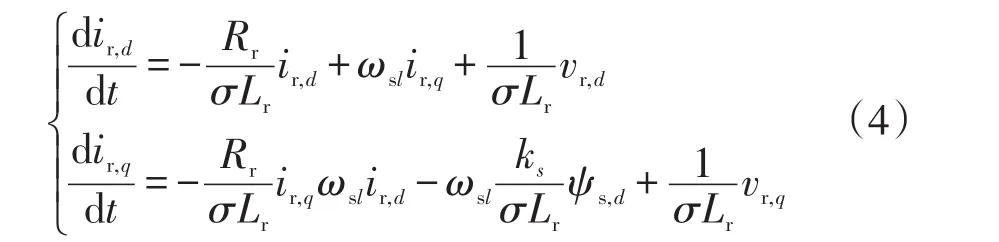
式中：ωsl为转差频率，ωsl=ω1-ωr；ωr为DFIG转子角频率；vr,d、vr,q为DFIG转子绕组的dq轴电压；ir,d、ir,q为DFIG转子绕组的dq轴电流；Rr、Lr分别为DFIG转子绕组的电阻和电感；ψs,d、ψs,q分别为DFIG定子绕组的d轴和q轴磁链；ks为定子耦合系数，ks=Lm/Ls；σ为漏磁系数，σ=1-L2m/LsLr。

若不计DFIG的RSC的开关损耗，则DC-link向DFIG转子绕组提供的功率Pr,dc为

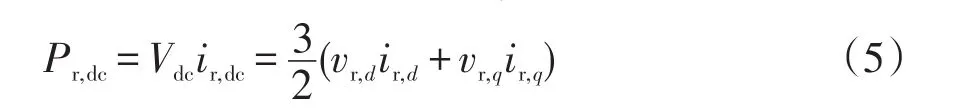
式中，ir,dc为DFIG的RSC直流侧的电流。

2 GSC控制策略

2.1 传统及改进的GSC控制策略

GSC的传统控制一般采用基于电网电压定向的双闭环矢量控制策略，其原理是通过调节GSC交流侧的d轴电流ig,d来控制DC-link的电容电压，传统的GSC控制策略框如图2所示。

由图2可看出，在设计控制器时仅对电网电压的外部扰动和GSC的内部扰动（交叉耦合项）进行了前馈补偿，没有考虑对DFIG转子绕组功率扰动的前馈补偿。文献[10]针对传统控制策略的不足，对GSC的控制策略进行了一定改进，对DFIG转子绕组功率扰动进行了前馈补偿，把此前馈补偿项施加在d轴的电流节点上，改进的GSC控制策略框如图3所示。

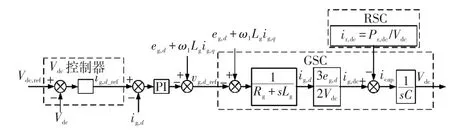
图2 传统的GSC控制策略框图Fig.2 Block diagram of the traditional control strategy for GSC

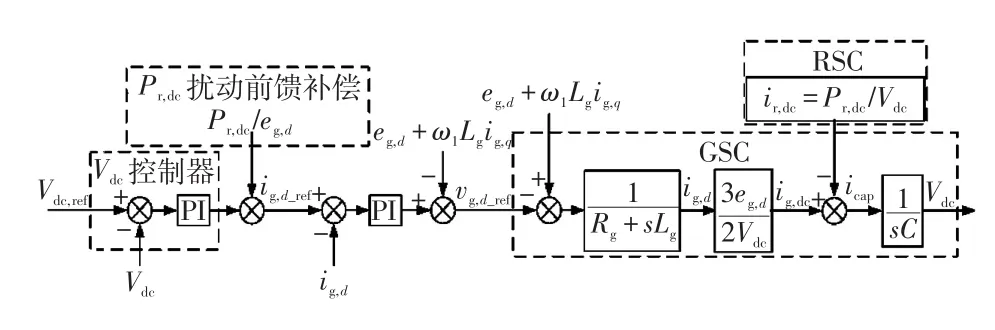
图3 改进的GSC控制策略框图Fig.3 Block diagram of the improved control strategy for GSC

由图3可看出，文献[10]虽然对DFIG转子绕组功率的扰动进行了前馈补偿，但这种前馈补偿行为不能完全补偿DFIG转子绕组功率的扰动且存在一定延时，这是由于在其前向通道中存在一个PI调节器以及一个动态延时环节1/(Rg+sLg)。

2.2 本文的GSC控制策略

针对上述控制策略的不足，本文提出一种快速且无延时完全补偿DFIG转子绕组功率扰动的GSC控制策略，以抑制DC-link电容电压的振荡。直接以DC-link电容器的充电功率为控制目标，如果控制DC-link电容器的充电功率为0，就可以保证DC-link电容电压保持相对稳定。本文提出的GSC控制策略仅采用一个功率控制环，可完全消除DFIG转子绕组功率扰动对DC-link电容电压的影响，其控制原理如下。

由图1可知，对DC-link电容器节点应用基尔霍夫电流定律可得

结合式（2）和式（3），由式（6）可推导出GSC交流侧的d轴电流ig,d为

式（7）代入式（1），可推导出GSC交流侧的d轴电压vg,d为

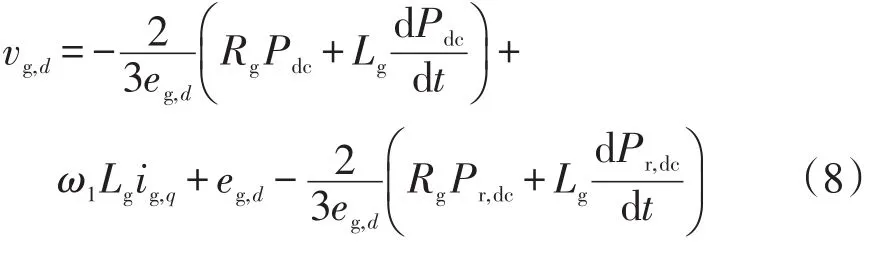
由式（8）可知，若直接以DC-link电容器的充电功率为控制变量，采用PI调节器，则可得GSC的d轴的控制策略为

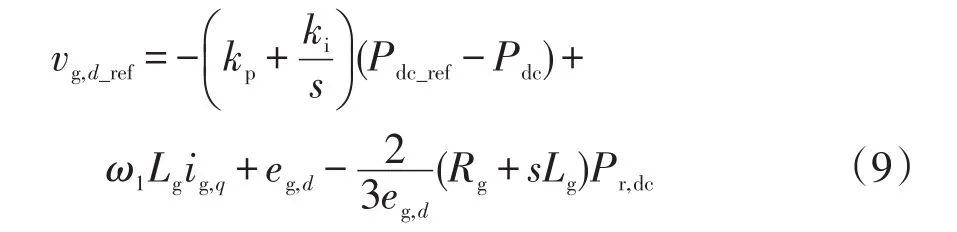
式中，kp、ki分别为比例和积分系数。

根据式（9）可得GSC的d轴直接功率控制框图如图4所示。

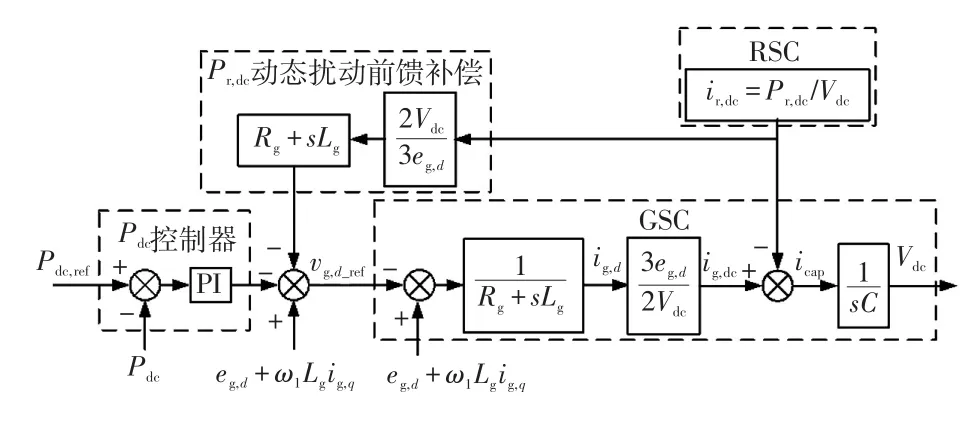
图4 GSC的d轴直接功率控制框图Fig.4 Block diagram of d-axis direct power control for GSC

GSC的q轴控制同传统策略一样，这里不再详细介绍，GSC的q轴控制框图如图5所示。

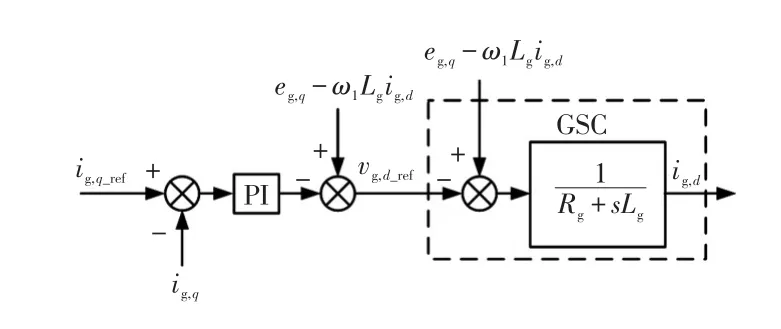
图5 GSC的q轴控制框图Fig.5 Block diagram of q-axis control for GSC

由图4可看出，在本文提出的控制策略通过直接控制DC-link电容器的充电功率，来达到控制DC-link电容电压的目的，并非上述两种控制策略中通过调节GSC的d轴电流ig,d来控制DC-link的电容电压，并且DFIG转子绕组功率扰动的前馈补偿是以电压的形式施加在d轴的电压节点上，而并非如上述改进的控制策略中以电流的形式施加在d轴的电流节点上。另外，在DFIG转子绕组功率扰动前馈补偿的前向通道中没有PI调节器，避免了PI调节器的响应延时，可完全补偿DFIG转子绕组的功率扰动。

然而，本文GSC控制策略中，DFIG转子绕组功率扰动前馈补偿时包含一个比例-微分环节Rg+sLg。为避免经典微分环节的噪声放大效应，本文引入一个跟踪-微分器来实现，其作用是尽快复原DFIG转子绕组功率Pr,dc并给出其微分信号。由文献[11]可知，“跟踪-微分器”具有的功能为给其个输入信号u(t)，可得到两个输出信号x1(t)和x2(t)，信号x1(t)跟踪输入信号u(t)，而信号x2(t)为输入信号u(t)的近似微分，即 x2(t)=x1(t)。根据文献[12]可构造出线性二阶跟踪-微分器的表达式为

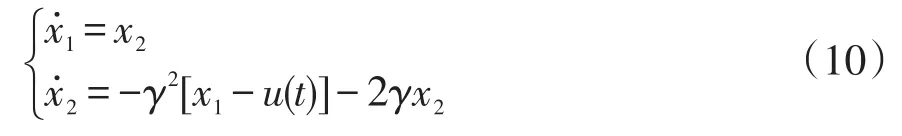
式中，γ为反映响应速度的调节参数。

跟踪-微分器对输入信号的跟踪及微分效果关键在于调节参数γ的确定，下面通过一个简单的例子来说明。设跟踪-微分器的输入为正弦信号u(t)=cos(πt)，在仿真中调节参数γ设定为采样频率时（本文取γ=10 000），仿真波形如图6所示，其具有良好的跟踪及微分效果。

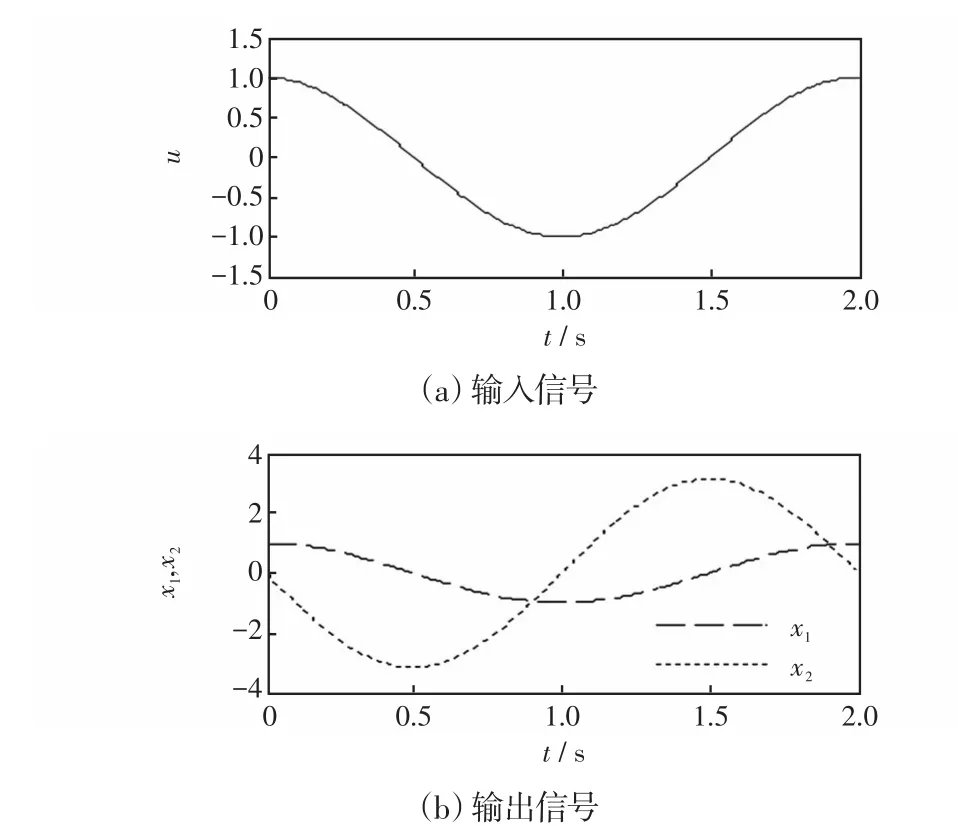
图6 跟踪-微分器的输入输出波形Fig.6 Input and output waveforms of tracking-differentiator

由图6可看出，本文所构建的跟踪-微分器能很好地跟踪输入信号并能较精确地给出其微分信号。

3 本文的GSC控制策略评估

为检验本文所提出的GSC控制策略的正确性以及对DC-link电压波动的抑制效果，在Matlab/Simulink仿真平台中构建了仿真模型，模型中DFIG的主要参数如表1所示。

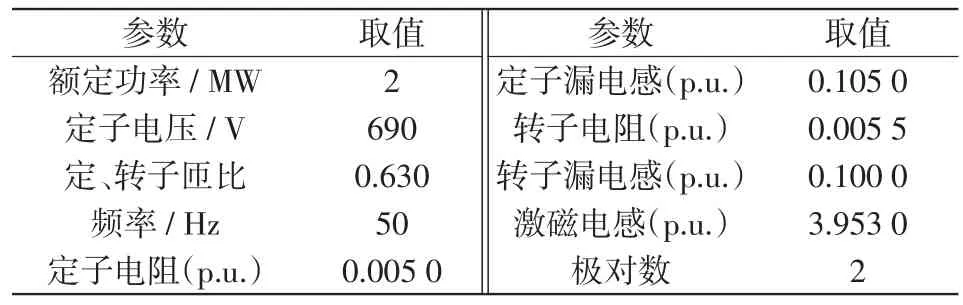
表1 DFIG的主要参数Tab.1 Main parameters of DFIG

3.1 电网电压正常情况下的评估

在电网电压正常情况下，验证所提出的GSC控制策略对DC-link电压波动抑制的效果，并与传统和改进GSC控制策略进行了对比研究。在此仅研究控制DFIG有功功率的转子q轴电流出现一个阶跃变化的情况。假设在t=4 s时ir,q从0.2 p.u.跃变到0.9 p.u.，其他运行条件保持不变，考察所提出的控制策略对DC-link电压波动抑制的效果。阶跃响应下转子绕组q轴电流ir,q及DC-link电容电压Vdc的动态波形如图7所示。

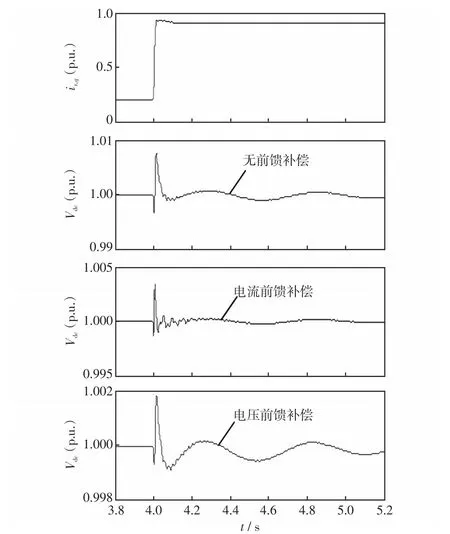
图7 阶跃响应下ir,q及Vdc的动态波形Fig.7 Dynamic waveforms ofir,qandVdcunder step response

由图7可看出，在电网电压正常情况下，由于DFIG有功功率的阶跃变化，将导致DC-link电容电压的轻微波动。对比3种GSC控制策略，本文所提出的控制策略具有较好的抑制效果。3种控制策略对DC-link电压幅值的抑制情况结果对比如表2所示。

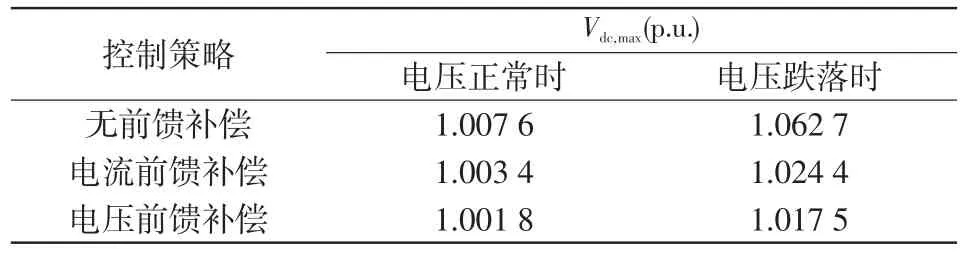
表2 结果对比Tab.2 Comparison among results

3.2 电网电压跌落情况下的评估

在此仅考虑电网电压三相对称跌落的情况，电网电压对称跌落前DFIG稳定运行在超同步状态（转差 s=-0.2）且功率因数为cos ϕ=0.9。在t=4 s时电网电压三相对称跌落至0.5 p.u.，电压跌落持续时间为0.5 s。DFIG网侧电压Vg及DC-link电容电压Vdc的动态波形如图8所示。

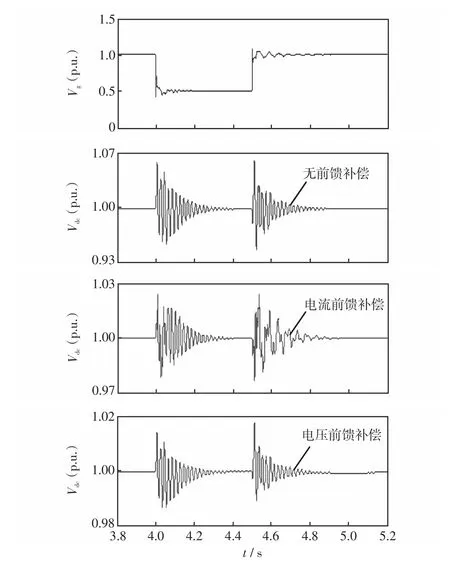
图8 电压跌落期间Vg及Vdc的动态波形Fig.8 Dynamic waveforms ofVgandVdcduring voltage dip

由图8可看出，在电网电压三相对称跌落期间，DC-link电容电压发生剧烈振荡，通过3种GSC控制策略的对比分析，本文所提出的GSC控制策略具有优良的DC-link电容电压波动抑制效果，并且对电容电压的振荡具有较强的阻尼，振荡衰减也很快。

4 结语

为快速抑制DFIG在外界扰动下DC-link电容电压的波动，本文提出了一种直接控制DC-link电容器的充电功率且无延时前馈补偿转子绕组功率扰动的GSC控制策略，详细地阐述了这种控制策略的控制原理并进行了仿真验证。为验证所提出的GSC控制策略对DC-link电压波动抑制的效果，对电网电压正常情况下DFIG有功功率阶跃变化的扰动和电网电压三相对称跌落引起的扰动进行了仿真评估。结果表明，本文所提出的GSC控制策略具有快速的瞬态响应速度及较强的振荡阻尼，有效地抑制了DC-link电容电压的幅值和振荡，协同RSC控制有助于DFIG故障穿越能力的提高。