基于改进下垂法的微电网逆变器并联控制技术

周奇勋，张 红，曹世宏，黎文权，曹浩翔，李 萌

（1.西安科技大学电气与控制工程学院，西安 710054；2.同济大学嵌入式系统与服务计算教育部重点实验室，上海 200092；3.总后勤部建筑工程研究所，西安 710054）

微电网系统中逆变器并联控制技术是微电网孤岛运行时实现高可靠性、高冗余性、高扩展性和高容量的基础，也是微电网孤岛运行时系统稳定运行的关键[1]。随着微电网系统的发展以及微电源的多样化，微电网中逆变器数量越来越多，采用有互联线的并联控制方式，逆变器之间的信号线会变得非常复杂。为了减少微电网中各逆变器之间的互联线以及解决有互联线控制抗干扰差的缺点，提出了逆变器无互联线并联控制技术，即下垂控制方法。然而，传统的逆变器下垂控制方法以线路电阻远远小于线路电抗为前提，并没有考虑不同逆变器线路阻抗不同的情况[2]。同时，传统逆变器下垂控制方法的基本控制方程推导过程中用到了逆变器并联公共节点PCC（point of common coupling）的电压。而微电网系统中各微电源配套的逆变器在地理位置上相距很远，导致反馈信号不可能测到等效线路阻抗后的PCC处电压，所以系统中的均流控制器不可能准确地实现下垂控制算法[3]。

基于传统下垂控制方法固有的缺点，国内外学者对传统下垂控制方法进行了改进。文献[4]提出了一种基于解耦的下垂控制方法，消除了有功功率和无功功率耦合对下垂控制的影响。但是，该下垂控制方法进行功率计算时需要利用线路的电抗和阻抗参数，对线路参数比较敏感。文献[5]提出了带虚拟阻抗的下垂控制方法，等效提高了逆变器输出阻抗的感性成分，均流方面效果明显，同时改善了逆变器的输出外特性，但是虚拟电阻过大会使线路压降增大，从而降低输出电压的幅值，降低电能质量，增加电路成本。文献[6]提出了谐波注入法的下垂控制方法，更好地实现了逆变器无功功率和谐波功率的均分。但是，谐波的引入会降低电能质量，增加了输出电压的谐波失真THD（total harmonic distortion）。

本文首先分析了传统下垂控制方法的原理及其不足之处，然后推导出基于逆变器输出端电压（不是PCC处电压）的有功功率和无功功率计算方程。为了使逆变器在不同电压等级输电线路（线路阻抗不同）上实现功率均分和环流抑制，同时为了提高系统的动态响应，本文提出了一种改进的逆变器并联下垂算法，并进行了仿真分析。仿真结果表明，该改进下垂控制法可以很好地实现逆变器的功率均分和环流抑制，提高系统响应速度。

1 下垂控制原理分析

传统下垂控制方法的思路来源于传统电网中同步发电机的自同步和电压下垂特性[7]。利用传统下垂控制方法中并联逆变器模块之间除了交流母线外没有其他信号线，增强了微电网孤岛运行时的抗干扰能力、冗余能力。目前，逆变器并联系统中有互联线控制技术无法克服地理位置受限、电磁干扰严重、冗余性不佳等先天性的缺点，从而促进了无互联线下垂控制方法在逆变器并联控制领域的发展。

由于微电网中存在各种分布式电源DG（dis⁃tributed generation），逆变器并联运行组成的微电网系统是一个复杂系统，下面以两台DG逆变器并联运行为例分析传统的无互联线下垂控制方法。图1为微电网系统孤岛运行时的实际拓扑，其中含有2个DG，即交流微电源和直流微电源，2个电压源型单相全桥逆变器，逆变器的输出通过LC滤波电路滤除电压高频成分，再经断路器连接至微电网交流母线上，断路器控制各DG的投切。

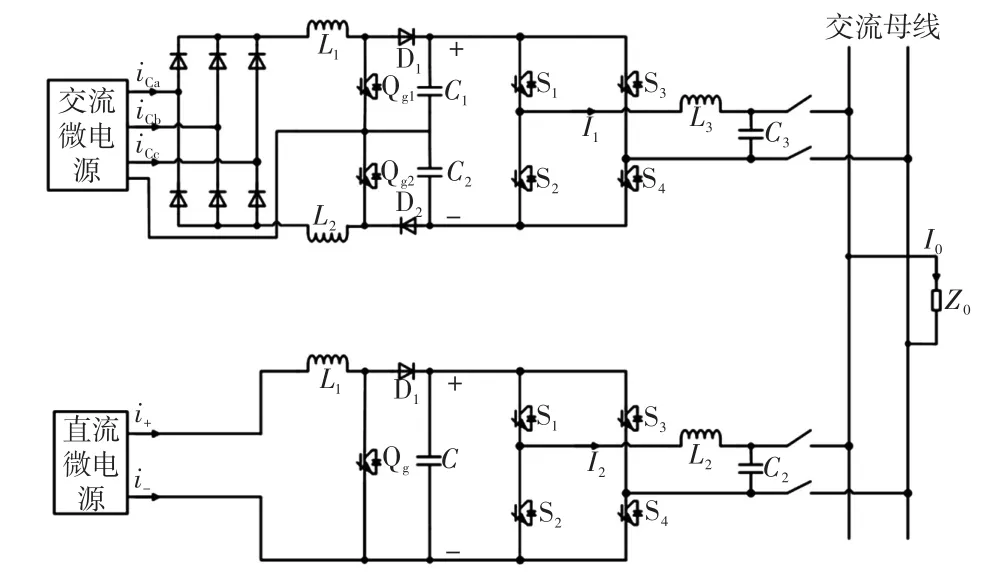
图1 微电网孤岛运行时的实际拓扑Fig.1 Real topology of microgrid in isolated island operation

为了便于分析，微电网中各台DG逆变器输出的交流电压可等效为可控电压源，图2为两DG逆变器并联等效电路。其中，R1、R2分别为DG逆变器1、2输出电阻和连接线路电阻之和；X1、X2分别为DG逆变器1、2输出电抗和连接线路电抗之和；Z0=R0+jX0为等效负载；V0∠0°为微电网系统中交流母线电压；V1∠δ1、V2∠δ2分别为逆变器1、2的输出空载电压；δ1、δ2分别为DG逆变器1、2输出空载电压与微电网交流母线电压的相位差。

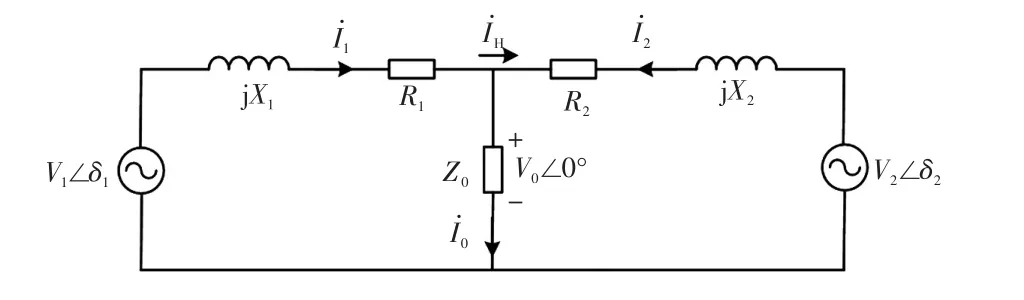
图2 两DG逆变器并联等效电路Fig.2 Parallel equivalent circuit of two DGs power inverters

由图2可得，单台DG逆变器输出电流为

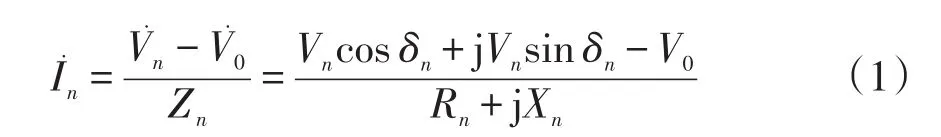
式中：n=1，2；Vn为DG逆变器n空载时输出的电压幅值；δn为DG逆变器n空载时输出电压与微电网交流母线的相位差；Zn为DG逆变器n输出阻抗和连接线路阻抗之和，Zn=Rn+jXn。

当X≫R时，由式（1）可得，单台DG逆变器输出复功率为

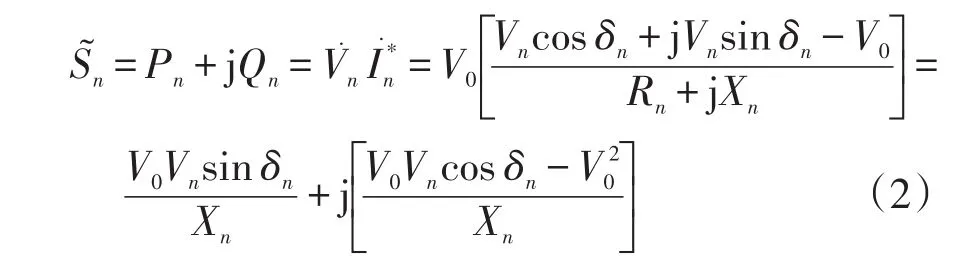
各DG逆变器输出的有功和无功功率分别为

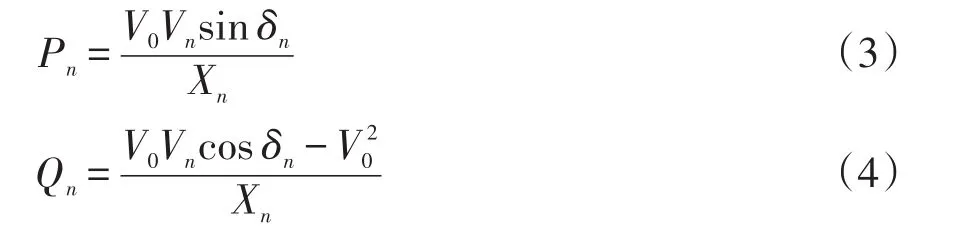
由于实际中Zn相比于Z0非常小，即Zn≪Z0，因此DG逆变器输出空载电压与微电网交流母线电压的相位差 δn很小，可近似认为 sin δn≈ δn，cos δn≈ 1。则式（3）和式（4）可简化为

实际中，电能质量供电电压允许偏差（GBT12325—2003）规定220 V单相供电电压允许偏差为标称系统电压的+7%、-10%，因此微电网交流母线电压的幅值V0变化范围不会很大。式（5）和式（6）表明，DG逆变器输出的有功功率与逆变器输出电压的相位差有关，无功功率与逆变器输出电压的幅值有关。电压相位差δn与角频率ωn满足如下关系：

因此，控制逆变器输出电压角频率可实现对电压相位差的控制，进而调节逆变器输出有功功率，控制逆变器输出电压幅值可调节逆变器输出无功功率。于是可得传统无互联线下垂控制方程为

式中：ω0,n、V0,n分别为DG逆变器输出空载电压的角频率和幅值；mn、nn为传统下垂法的下垂控制系数；ωref、Vref为合成参考电压的角频率和幅值。

通过对传统下垂法进行分析可知：①传统下垂法各逆变器输出有功功率和无功功率的计算用到了逆变器并联PCC处的电压。而微电网中各DG用逆变器相距很远，由于反馈信号的限制不可能测到等效线路阻抗后的PCC处电压，所以传统下垂法抗干扰性低、响应速度慢、控制精度低。为了解决逆变器并联PCC处电压不好采集的缺点，有必要对传统无互联线控制方法中功率计算环节进行改进。②传统下垂法控制方程是以逆变器输出阻抗和连接线路阻抗之和为感性的前提下推导得到。但是，不同电压等级的电网线路有不同的阻抗比，如表1所示[8]。可见，在低压线路中，电阻在阻抗中占很大比例，即阻抗比相对中高压线路较高。由于微电网中与每台逆变器的连接线路长度存在差异，线路越长、阻抗越大，在低压线路中线路电阻占阻抗的比例就越大，利用传统下垂法进行负载功率均分时，在稳定运行状态下，并联逆变器的输出电压频率相等，则有功环流几乎为0，但是线路阻抗不一致，各逆变器连接线路上的电压降也将不相等，致使各逆变器输出电压幅值不相等，则无功环流很大。为了解决逆变器连接线路阻抗不一致的情况，有必要对传统无互联线下垂控制方法进行改进。

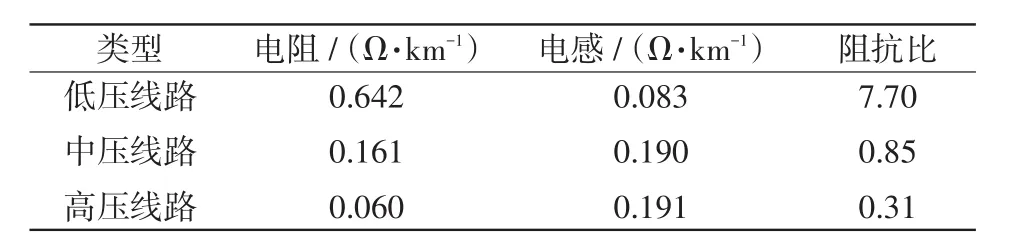
表1 不同电压等级的电网线路阻抗比Tab.1 Comparison of line impedance ratio at different voltage levels

2 改进下垂控制原理

2.1 改进功率计算

本文在计算微电网系统中各DG逆变器输出功率时采用逆变器输出端电压，即图2中的V1∠δ1、V2∠δ2，并未采用PCC处电压V0∠0°，这样就解决了传统下垂法采用PCC处电压的缺点。若n台DG逆变器并联，根据KVL和KCL定律可得

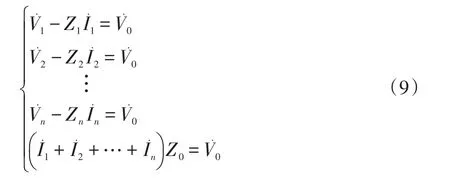
由式（9）可推导出负载端电压（即PCC处电压）的向量表达式为

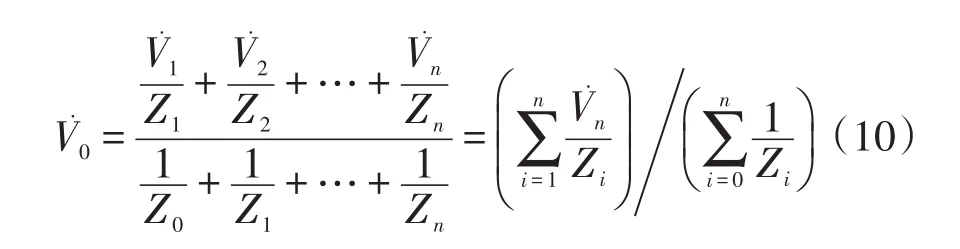
因此，可由KVL定律推导出第n台逆变器输出电流的向量表达式为

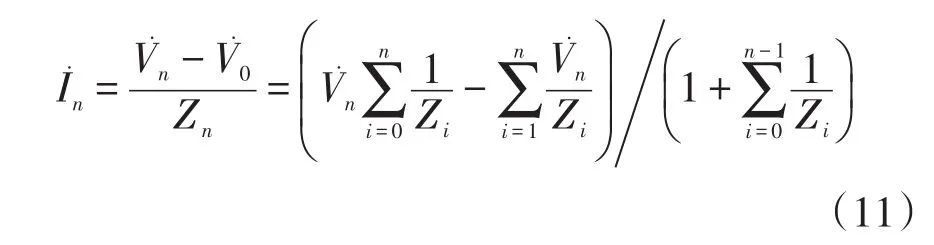
由视在功率计算公式可得，第n台逆变器输出视在功率的表达式为

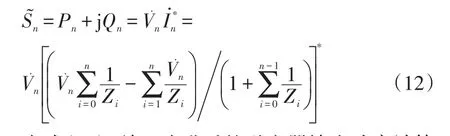
由式（12）可知，改进后的逆变器输出功率计算只与逆变器端电压有关，并未采用PCC处电压，这样就克服了采集并联PCC处电压的困难。

2.2 改进下垂控制方法

当微电网系统孤岛运行时，受不同电压等级连接线路阻抗不同的影响，连接线路压降不相等，负载的无功功率不能实现理想均分，使得线路中产生无功环流。为了抑制线路阻抗不同引起的无功环流，根据逆变器输出功率和线路阻抗设计了线路压降补偿环节，使逆变器输出电压升高，抵消连接线路电压降，实现不同电压等级连接线路末端电压相等，从而有效抑制线路阻抗不同引起的无功环流，实现负载的无功功率理想均分。图3为改进下垂控制方法线路压降补偿环节，其中为经线路压降补偿环节后逆变器输出电压的幅值。

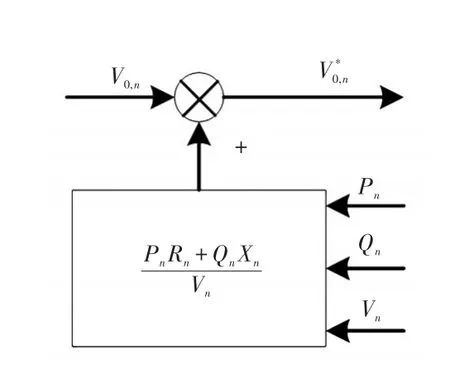
图3 改进下垂控制方法线路压降补偿环节Fig.3 Line voltage drop compensation link usingimproved droop control method

由上述分析可知，为了抑制线路阻抗不同引起的无功环流，本文在传统下垂控制法的基础上引入线路压降补偿环节。线路压降补偿环节直接利用逆变器输出端电压、电流以及电网线路每千米阻抗值估算出逆变器并联PCC处电压，而传统下垂法需利用反馈线路采集PCC处电压信号，抗干扰性低、响应速度慢、控制精度低。因此，线路压降补偿环节有效抑制线路阻抗不同引起的无功环流，实现负载无功功率理想均分。同时，在下垂控制法中，功率计算需要经过一个低通滤波器，而低通滤波器将降低并联系统的动态调节性能，为了提高微电网系统中各逆变器并联控制系统的动态性能，本文在下垂控制方程中引入积分环节和微分环节。积分环节是为了实现指令频率和指令电压无差控制，这样将使线路阻抗不平衡、各并联逆变器单元参数不一致以及逆变电源输出频率波动等干扰因素得到补偿，系统有功功率和无功功率可以获得较优的分配效果。微分环节提高逆变器并联控制系统动态响应的速度，并且逆变器有功功率、无功功率的计算采用LC滤波器后的电压和电流信号，大量的干扰信号被滤波器滤除，微分环节的输入信号比较干净，引入微分不会对整个控制系统产生干扰。微分参数的选取需对逆变器改进下垂法进行建模后得到有功-频率下垂和无功-幅值下垂的特征方程，并对其根轨迹分析选择合适的微分系数。基于以上结论，本文提出一种改进的下垂控制方法，其下垂控制方程为

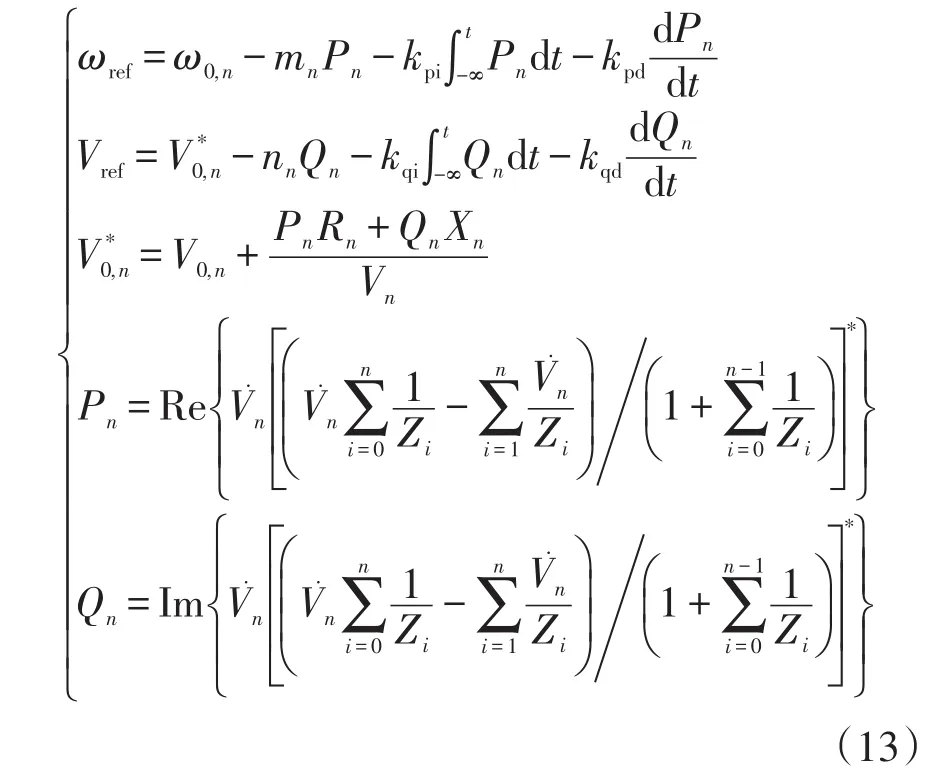
式中：kpi、kqi分别为有功功率积分系数和无功功率积分系数；kpd、kqd分别为有功功率微分系数和无功功率微分系数。

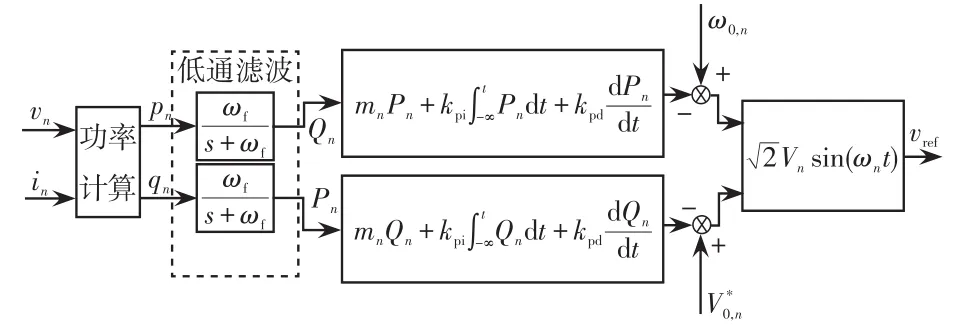
图4 改进下垂控制方法结构框图Fig.4 Block diagram of improved droop control method

图4为改进下垂控制方法结构框图，其中ωf为低通滤波器的截止频率，Vref为下垂控制环节输出电压。图5为单台逆变器双闭环控制结构框图[9]，其中IL,n为LC滤波后的电流，Vm为脉冲调制解调环节调制信号。

图5 单台逆变器双闭环控制结构框图Fig.5 Block diagram ofone single inverter with dual closed-loop control

3 系统仿真与分析

为了验证改进下垂控制方法理论的正确性和可行性，本文以两台电压源型单相逆变器并联系统为例，用Matlab/Simulink进行仿真验证。微电网中逆变器并联采用电压电流双闭环控制策略，电压电流环都采用PI控制，以保证逆变器输出端电压等于改进下垂法合成参考电压，且动态响应快。为了验证改进下垂法在线路阻抗不相等的情况下能很好地实现负载功率均分，仿真中设定两台逆变器不同的输出阻抗。具体仿真参数如下：两逆变器输出电压峰值为230 V，频率为50 Hz；滤波电感 L1=0.1 mH，L2=0.12 mH ，滤波电容 C=10 μF ；仿真时间T=0.4 s。

图6为微电网中逆变器1正常运行状态下，在T=0.2 s突然投入逆变器2时两逆变器的稳态输出电流及环流波形。仿真过程为负载恒为5 Ω时，在逆变器1输出电压峰值为230 V及频率为50 Hz的基础上，在T=0.2 s时并联另一台输出电压峰值为230 V及频率为50 Hz的逆变器2。由图6（a）和图6（b）可以看出，在T＜0.2 s时逆变器1的电流约为46 A，逆变器2的电流约为0 A；在T＞0.2 s时逆变器1的电流约为23 A，逆变器2的电流约为23 A，并且在T=0.2 s时逆变器并联系统响应速度快且过渡平滑。微电网系统环流为由图6（c）可以看出，在T＞0.2 s时系统环流几乎为0。图7为逆变器2投入时微电网交流母线电压和负载电流，可以看出，不管是逆变器1单独运行还是逆变器1、2并联运行，微电网交流母线的电压峰值都维持在230 V左右，负载电流维持在46 A左右。

由上述分析可知，采用改进后的下垂控制方法，两逆变器并联运行时能够实现理想均流，微电网中环流很小，并且动态响应速度快且过渡平滑。

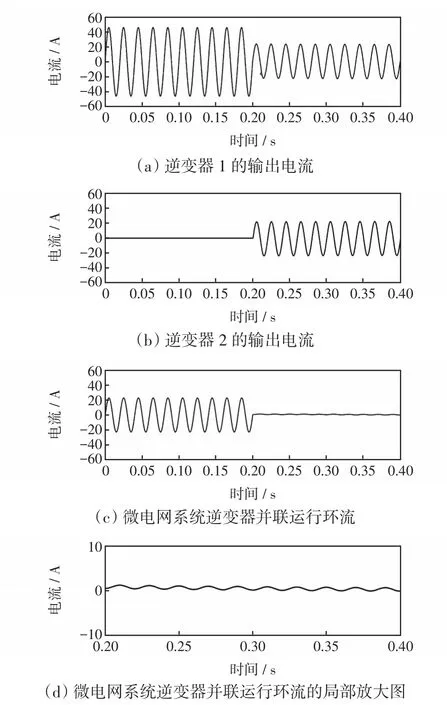
图6 微电网中逆变器投入时逆变器的输出电流及环流Fig.6 Output currents and circulating current when the inverter is put into operation in microgrid

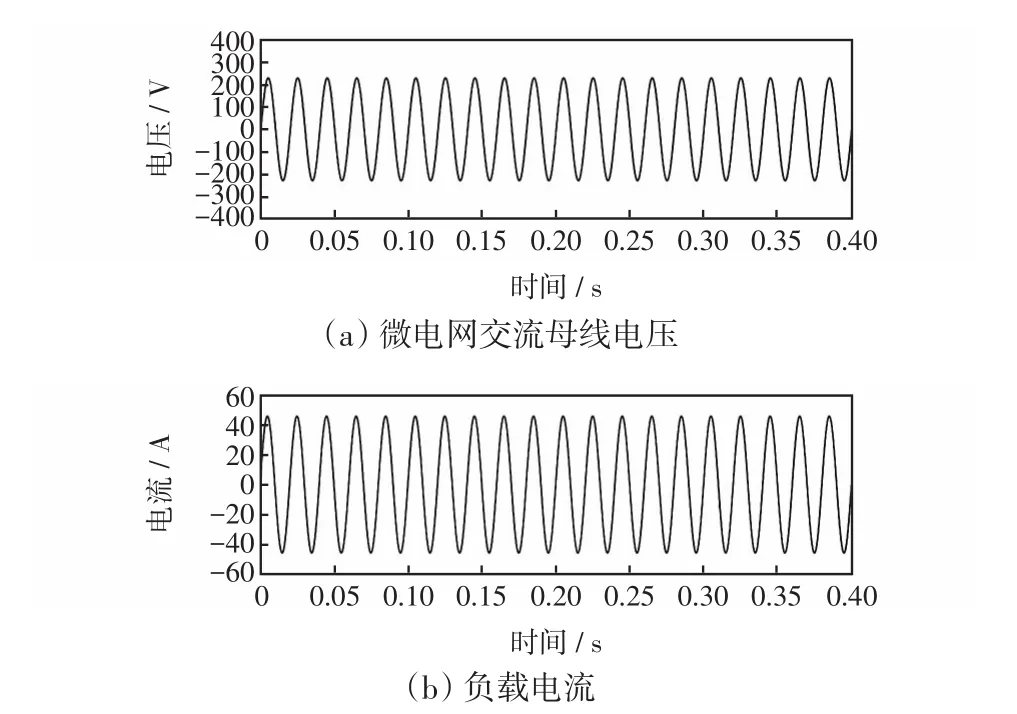
图7 微电网中逆变器投入时交流母线电压及负载电流Fig.7 AC bus voltage and load current when the inverter is put into operation in microgrid

图8为微电网中负载突变时两逆变器的稳态输出电流及系统环流波形。仿真过程为逆变器1、2并联运行，负载为10 Ω，在T=0.2 s时微电网再投入10 Ω的负载，使得总负载为5 Ω。由图8可以看出，当T=0.2 s时总负载突变为原来的1/2，则逆变器1、2输出的电流突变为原来的2倍，并且在逆变器并联运行的整个过程中，微电网环流很小。由图9可以看出，微电网中负载突变时交流母线电压峰值依然维持在230 V，负载电流突变为原来的2倍，并且逆变器1、2输出电流之和等于负载电流。

由上述分析可知，采用改进后的下垂控制方法，负载突变前后微电网能保持较好的均流性能，并且动态响应速度快、过渡平滑。

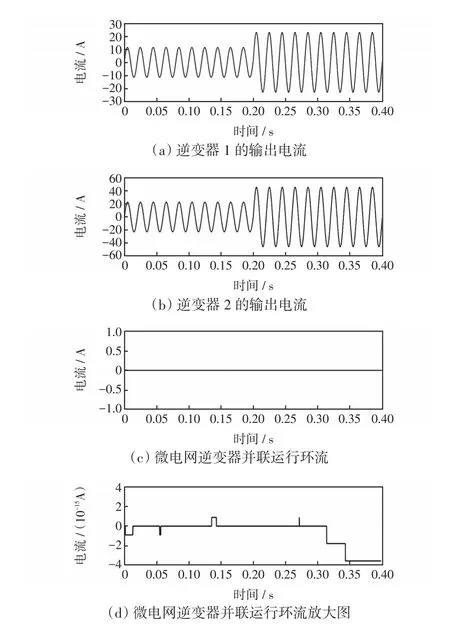
图8 微电网中负载突变时逆变器的输出电流及环流Fig.8 Output currents and circulating current of the inverter in microgrid with load mutation

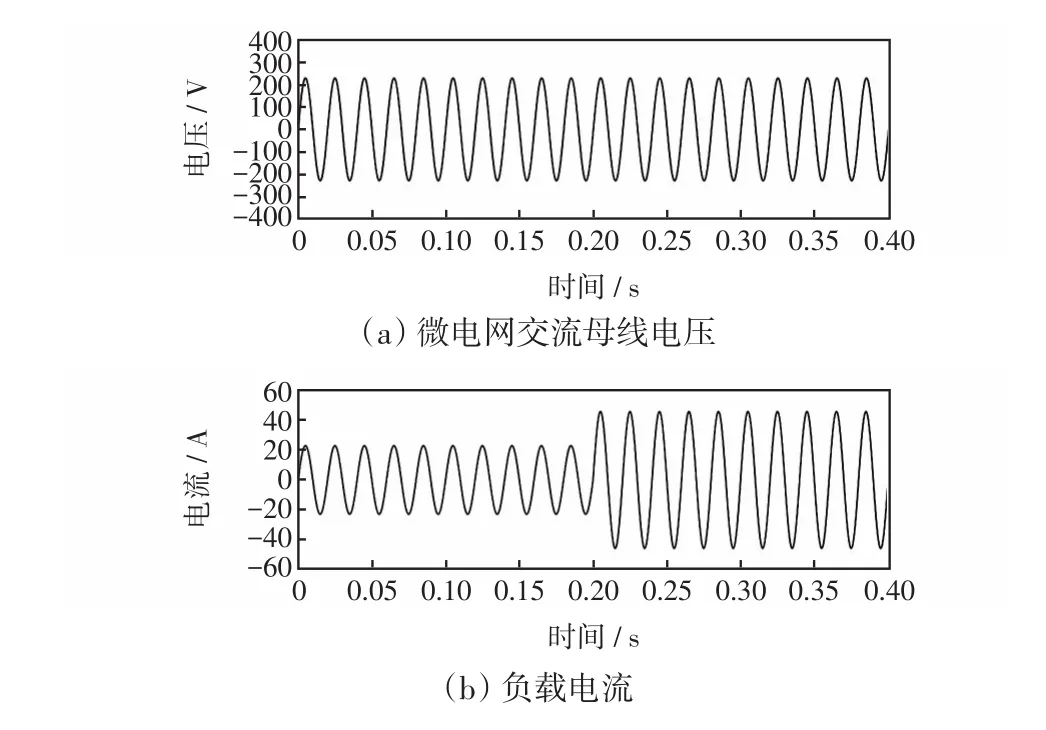
图9 微电网中负载突变时交流母线电压及负载电流Fig.9 AC bus voltage and load current of microgrid with load mutation

4 系统实验与分析

在实验室搭建由两台相同容量的电压源型单相逆变器组成的微电网实验平台。其中，控制芯片采用TI公司的TMS320F28335，两逆变器输出电压峰值为230 V，频率为50 Hz，滤波电感L1=0.1 mH，L2=0.12 mH，滤波电容C=10 μF。图10为微电网实验平台中逆变器1正常运行状态下，突然投入逆变器2时逆变器2的稳态输出电流及系统环流波形。图11为突然投入逆变器2时微电网实验平台交流母线电压，不管是逆变器1单独运行还是逆变器1、2并联运行，微电网交流母线的电压峰值都维持在230 V左右。

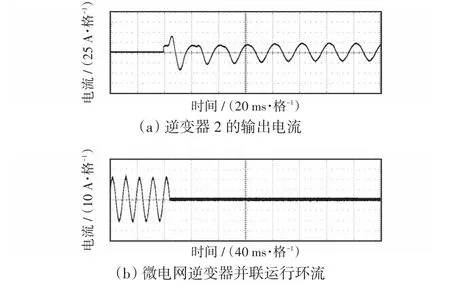
图10 微电网实验平台中逆变器投入时逆变器的输出电流及环流Fig.10 Output current and circulating current whenthe inverter is put into operation in microgrid platform

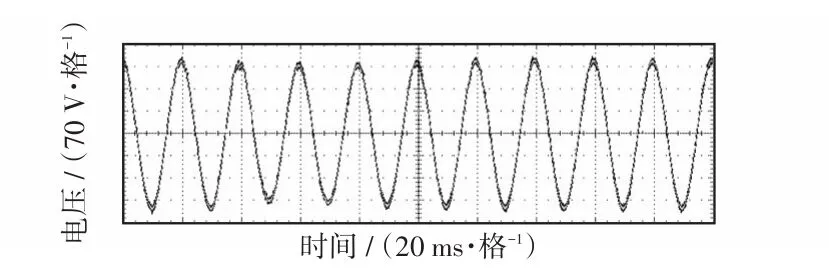
图11 微电网实验平台中逆变器投入时交流母线电压Fig.11 AC bus voltage whenthe inverter is put into operationin microgrid platform

由上述分析可知，采用改进后的下垂控制方法，两逆变器并联运行时微电网系统中的环流很小，能够实现理想均流。从逆变器2的输出电流可见，突然投入逆变器时，微电网需一段很小的调节时间才能使并联系统稳定运行。总体来看，采用改进后的下垂控制方法，实现了系统的理想均流，提高了动态响应速度。

图12为微电网实验平台中逆变器1、2并联运行状态下，负载突变时系统的环流波形和微电网交流母线的电压。由图12可知，当逆变器1、2并联运行时，负载的投切对并联运行系统影响很小，系统环流维持在很小的范围，交流母线电压峰值维持在230 V。

由上述分析可知，采用改进后的下垂控制方法，负载突变前后微电网系统能保持先前的稳定运行状态，几乎不受负载投切的影响，并且动态响应速度快且过渡平滑。

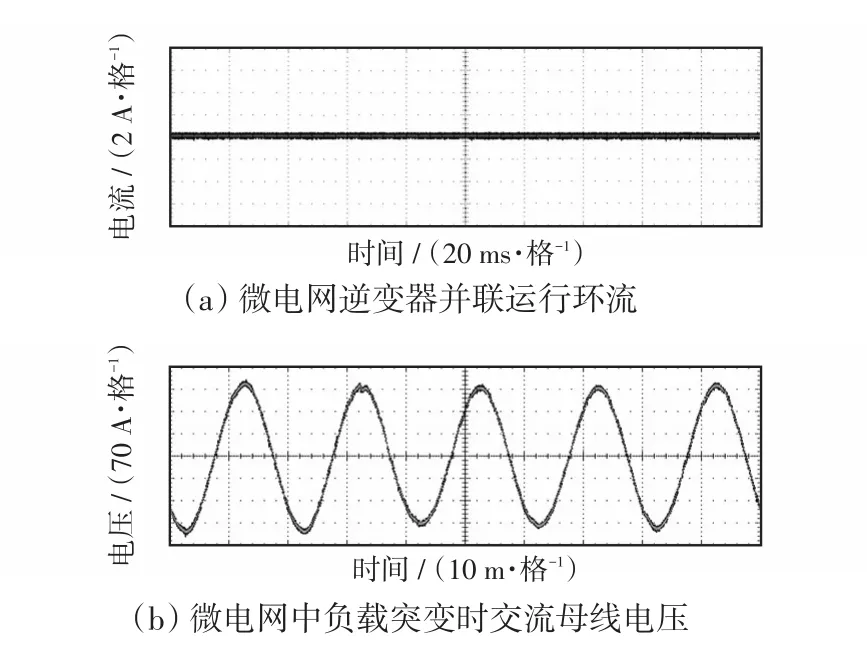
图12 微电网实验平台中负载突变时系统环流及交流母线电压Fig.12 Circulating current and AC bus voltage of microgrid platform with load mutation

5 结论

（1）本文基于逆变器输出端电压推导出了多台逆变器并联时各台逆变器输出功率计算公式，提高了微电网逆变器并联均流控制器的控制精度，使得功率均分的精度提高。

（2）本文在传统下垂控制方法的基础上增加了线路压降补偿环节，消除了不同电压等级连接线路阻抗不同引起的无功环流，使得逆变器并联系统具有较好的均流性能。

（3）本文在传统下垂控制方法中增加了积分环节和微分环节，消除了利用低通滤波器计算功率时对并联系统动态响应的影响，使得并联系统动态响应速度快且静态误差小。