递归随机子空间辨识方法在电力系统区间振荡模式估计中的应用

黄宏亮，和 萍

（1.浙江大学电气工程学院，杭州 310027；2.郑州轻工业学院电气信息工程学院，郑州 450002）

区间振荡的存在严重限制了互联电网电能的传输能力，其所造成的大停电事故不仅在国内时有发生[1-2]，在全世界范围内也有事故记载[3-5]，这充分显示出区间振荡对于整个电网的潜在破坏力。因此，分析和监测区间振荡对于维持电力系统稳定运行至关重要。近年来，随着同步相量测量单元PMU（phasor measurement unit）等新技术的兴起[6]，利用量测数据估计和分析区间振荡模式逐渐成为主流研究方向[7]。

电网正常运行时获取的量测信号被称为类噪声数据，因为此时系统输入为负荷的随机小变动。电网在发生故障后进入暂态时所获取的量测信号被称为Ringdown数据，此时系统输入由短路、发电机跳闸或甩负荷所引起，其中包含有较高密度的振荡信号。基于量测数据来估计和分析区间振荡的方法通常可以根据适用的数据类型（类噪声数据和暂态数据）分为两类[8]。例如，Prony方法[9-10]、特征系统 实 现 算 法 ERA（eigensystem realization algo⁃rithm）[11-12]以及矩阵束（matrix pencil method）[13]常被用于处理暂态数据来估计和分析暂态电网中的低频振荡模式，而YW（Yule-Walker）[14]、R3LS（regu⁃larized robust recursive least squares）[15]、子空间辨识方法[16]等常被用做处理类噪声数据来估计和分析准稳态电网中的区间振荡模式。电力系统运行于一个平衡点时总会受到小的负荷变动，因此基于类噪声数据的估计方法更为有用[14，17]。

随机子空间辨识SSI（stochastic subspace identi⁃fication）方法在利用类噪声数据估计区间振荡模式IOM（inter-area oscillation mode）上具有许多优点。首先，辨识出的系统模型为状态空间形式，有利于估计、预测和控制[18]；其次，利用SSI方法估计出的振型（mode shape）较为准确，而振型有助确定振荡模式的主导传递通道以及振荡源[19]；再次，SSI方法便于模型阶数的选择[20]、处理庞大数据以及系统动态的变化[21]。然而其中奇异值分解SVD（singular value decomposition）过程的大计算量成为SSI方法应用于区间振荡在线估计和追踪的最大弱点。

针对这一缺点，本文将采用递归随机子空间辨识 RSSI（recursive stochastic subspace identification）方法来在线估计和追踪低频振荡模式，该方法只需在初始化时确定模型阶数，通过直接更新扩展能观性矩阵，避免反复进行SVD，大大降低了计算量。同时，本文也考虑了模型阶数在在线估计和追踪中的修正，提高了估计的准确性。

1 SSI方法用于IOM特性估计的算法描述

SSI被广泛用于多输入多输出MIMO（multipleinput multiple-output）系统，最主要的原因在于其能够直接通过输入输出数据辨识出系统的状态空间模型。该方法的基本思想是将系统输出矩阵的行空间作为系统输入矩阵行空间的投影，构造Hankel矩阵，再利用SVD方法得到系统的一组实现[A B C D]。在本节中将介绍如何利用SSI方法估计互联电网中的IOM。

在多数运行情况下，电力系统工作在一个平衡点附近（受到负荷小幅随机波动的影响，而这种波动可视为系统中的类噪声）。在分析低区间振荡问题时，忽略原动机的作用，并在平衡点处对系统做线性化处理。假设以nb条母线的电压相角作为系统输出，系统模型的状态空间形式可以表示为

式中：A为系统矩阵；C为输出矩阵；x(k)、y(k)、w(k)和v(k)分别为第k时刻系统的状态向量、输出向量、过程和测量噪声向量。系统输出协方差Han⁃kel矩阵可以表示为

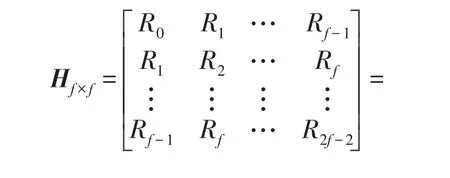
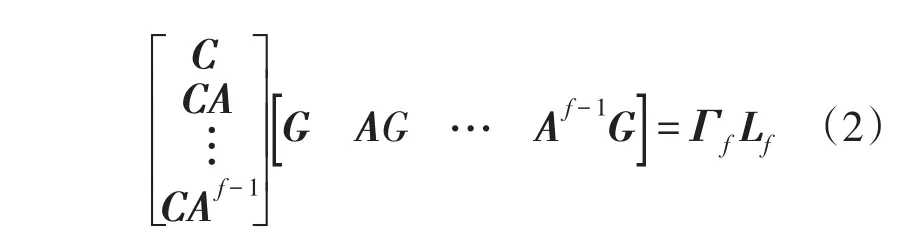
式中：Ri=E{y (k)yT(k-i)}，Ri＞0，E{}为期望计算；G为矩阵，其中Gi=E{x (k)yT(k)}；Γf和 Lf分别为系统的扩展能观性矩阵和能控性矩阵。协方差Hankel矩阵理论上应为无穷维数，但在实际过程中，选取数据总长度M的一半，即2f=M。根据测量得到的协方差 Ri,i=1,2,…,2f－2，可以得到协方差Hankel矩阵的估计值H为

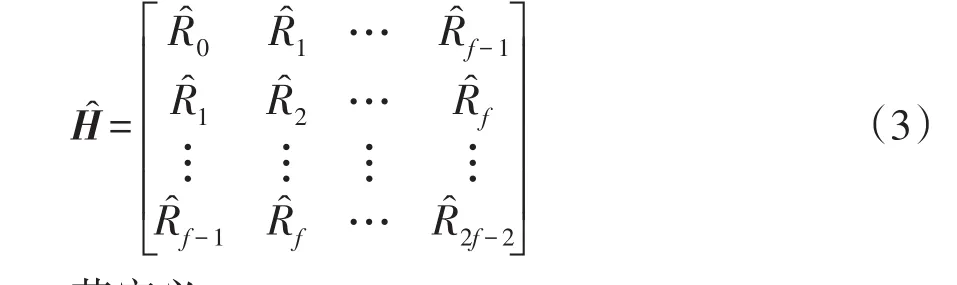
若定义

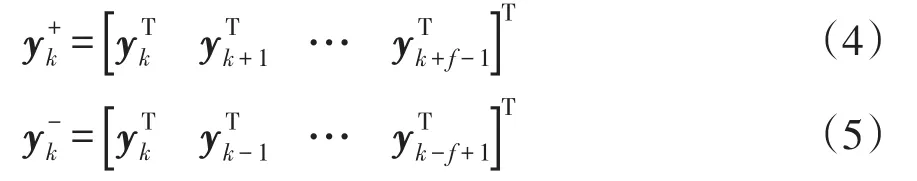
则式（3）可以改写成

式中：k涵盖了各组数据；p为标准化参数（normal⁃ization parameter）。文献[22]指出由于乘以1个系数不会影响到系统矩阵和输出矩阵的估计值A和，因此 p通常被取为1。

H是高维矩阵，采用SVD方法将其降维[23]，可表示为

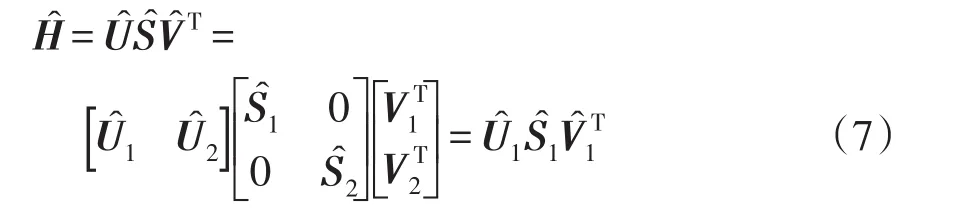
式中：U、V为正交矩阵；U1、U2分别为U矩阵的分块矩阵；V1、V2分别为V矩阵的分块矩阵；S为中间矩阵；S1、S2分别为S的对角矩阵；＾表示估计值。S1∈Rn×n为奇异值组成的对角矩阵，且奇异值沿对角线降序排列，选取最大的n个奇异值的方法有许多，比如赤池信息量准则AIC（Akaike’s infor⁃mation criterion）[24]，贝叶斯信息准则 BIC（Bayesian information criterion）[25]等。本文选用方法为奇异值准则 SVC（singular value criterion）[20]。由此可以得到能观性矩阵Γf的估计值为

式中，fs为采样频率。相对应的频率和阻尼的估计值和分别为

2 SSI方法的递归形式

SSI方法应用于电网IOM估计的一个不足之处在于其奇异值分解的计算量较大。为此，在本节中，将给出SSI的递归形式以克服这一缺点。RSSI方法的核心思想就是利用获得的新时刻的数据直接更新，从而避开计算量较大的奇异值分解步骤。假设初始的输出数据为{y1,y2,…,yN} ，根据第1节中所述方法，可以利用SVC确定模型阶数N。那么，在新时刻N+1时，可以根据和更新Hankel矩阵。文献[22]指出无论是用指数遗忘形式，窗口滑动形式或者是组合的形式来更新，其更新形式都可以描述为

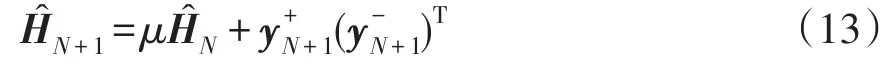
式中，μ为遗忘因子。考虑以下最小值问题[26]，可表示为

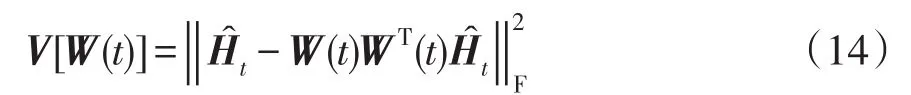
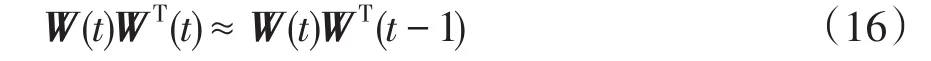
这样可以得到递归形式为

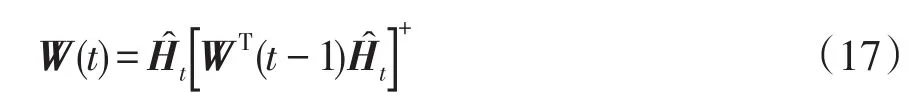
式中，[]+表示求广义逆运算。

文献[27]指出递归运算如式（17）所示，较近似前的递归形式具有更好的追踪性能。同时，文献[27]中提出了更加简洁的方法，即利用第t时刻的输出数据向量取代与WT(t-1)相乘。本文所采用的递归形式算法的具体步骤如下。

步骤1 根据初始值计算，可表示为

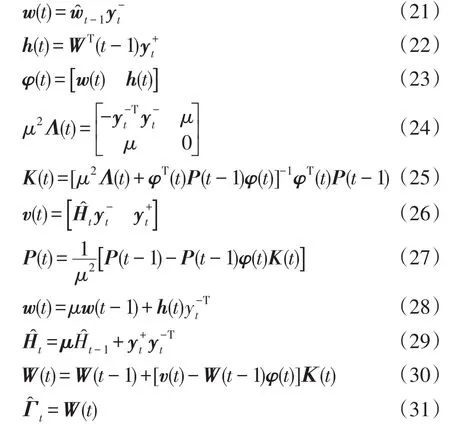
步骤3 重复步骤2，直至包含所有时刻数据。

3 数值例子

在本节中，分别通过四机系统和美国东北部NPCC48机（Northeastern Power Coordinating Council 48-machine）系统来验证SSI方法处理暂态数据的准确性以及其递归形式在线估计IOM时的准确性。需要说明的是，本节所用四机系统和NPCC48机系统为标准仿真测试系统，其中所用测量数据为母线电压相角，与PMU测量数据相同，但并非真实PMU数据。

3.1 四机系统

如图1所示，四机系统中共有4台发电机（本文中的发电机G1～G4均安装了调速器和电力系统稳定器PSS（power system stabilizer）和13条母线。系统中共有3个低频振荡模式包括G1与G2之间区域内振荡模式、G3与G4之间的区域内振荡模式以及G1G2与G3G4之间的区间振荡模式。

本文只研究IOM的估计问题。仿真总时间长度为2 000 s，步长为0.01 s。母线4上始终加入负荷波动，在第1 000.1 s时在母线3和母线101之间的一回线设置了三相故障并于第1 000.2 s时清除该故障，此时系统结构恢复到故障之前，系统将经过大幅振荡的暂态过程后重新进入新的准稳态。

整个过程可以分为3个阶段：第1阶段为大扰动前的准稳态；第2个阶段为扰动发生后系统历经的暂态阶段；第3个阶段为扰动后系统再次进入的准稳态。选取母线1、3、13和101的电压相角为系统输出，并在每个阶段中选取200 s的时间长度，分别对这3个阶段采用SSI方法对低频振荡模式的频率和阻尼进行估计，结果如表1所示。

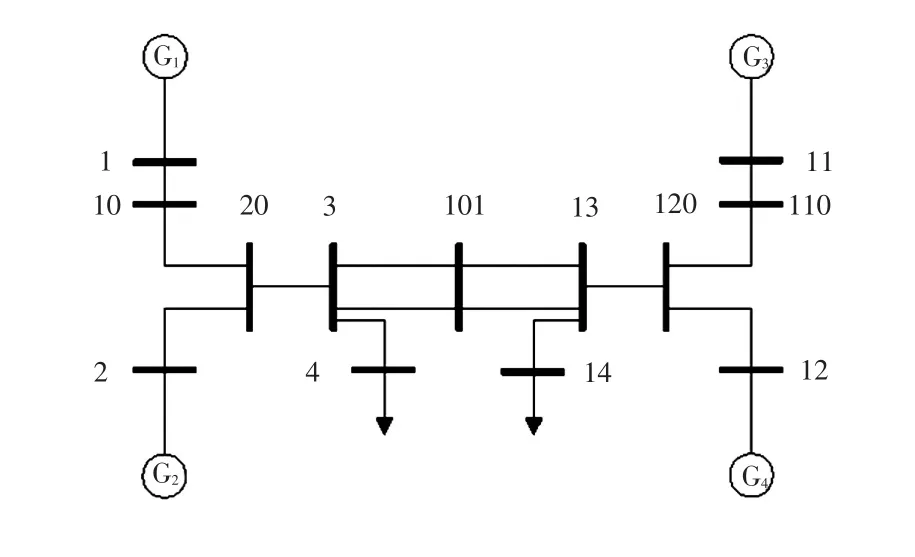
图1 四机系统的单线图Fig.1 Single-line diagram of four-machine system

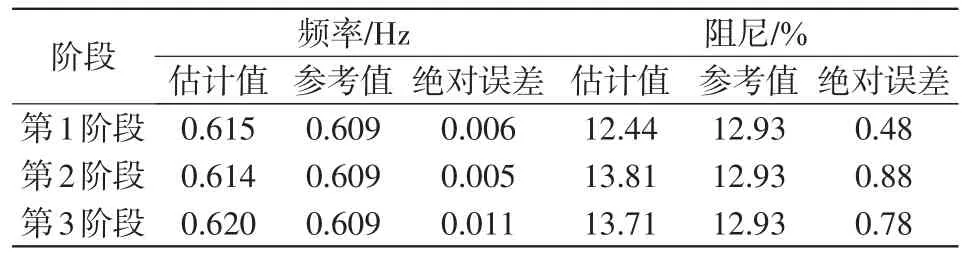
表1 四机系统故障前后IOM估计结果Tab.1 IOM estimation results of four-machine system before and after fault

表1中参考值是通过全阶物理模型计算得到。由表1可知，SSI方法不仅对类噪声数据结果处理准确而且对故障后的暂态数据也同样处理准确。

然后考虑采用RSSI方法对IOM进行在线估计。取前500 s数据为RSSI方法提供初始值，并在之后的1 000 s内每隔0.2 s对IOM进行估计，考虑不修正模型阶数。图2为在线估计结果，实线为采用RSSI方法的估计值曲线，虚直线为参考值，可见采用RSSI方法能在故障前后得到准确的频率和阻尼估计值。

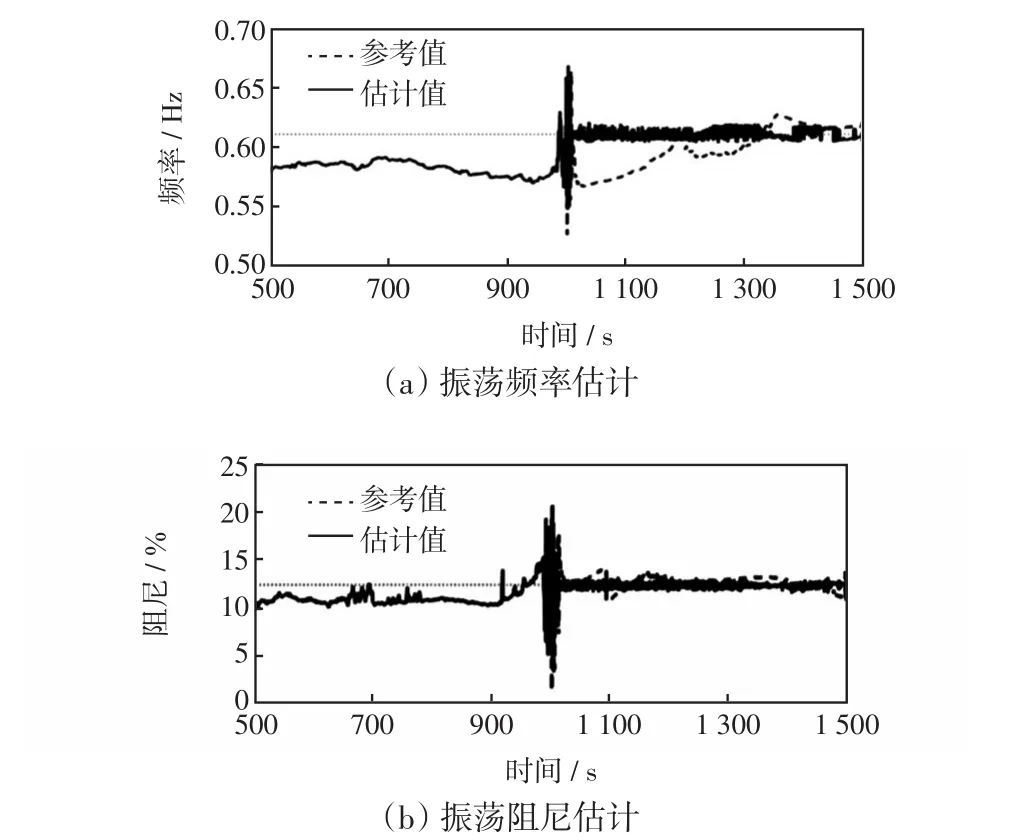
图2 RSSI四机系统区间振荡估计结果Fig.2 IOM estimation results of four-machine system via RSSI

3.2 NPCC48机系统

RSSI方法可以被应用于更大的电力系统。本文以NPCC 48机系统为例，说明RSSI方法在复杂电力系统中估计多个振荡模式的准确性。48机系统是由140条母线以及48台发电机组成。文献[28]利用模态分析方法将系统划分为9个区，8个区间振荡模式的频率与阻尼参考值见表2。

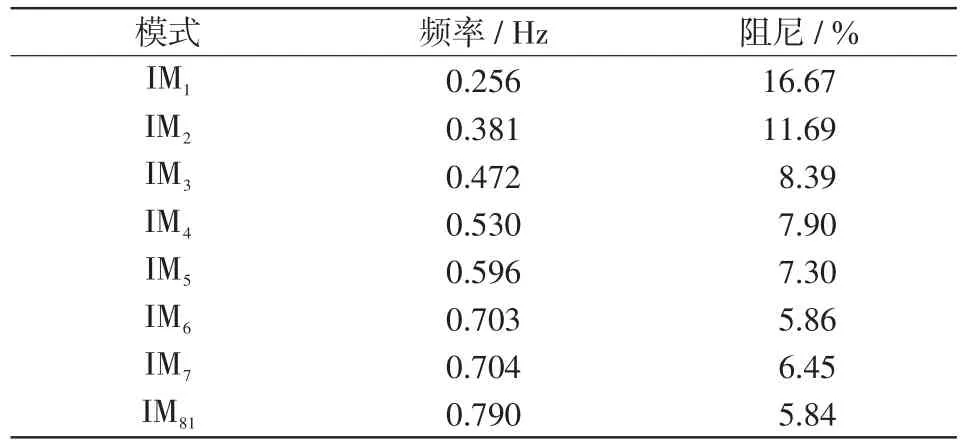
表2 NPCC48机系统IOM频率与阻尼参考值Tab.2 Reference values of IOM frequency and damping for NPCC 48-machine system

采用RSSI对IM1、IM2和IM3模式进行估计。选取这3个模式进行估计是因为其频率较低，且涉及的发电机较多。与四机系统的例子相似，设定仿真总时间长度为2 000 s，步长为0.01 s。母线4上始终加入负荷波动，在第1 000.1 s时在母线3和母线4之间的一回线设置了三相故障并于第1 000.2 s时清除该故障，此时系统结构回复到故障前，系统经过大幅振荡的暂态过程后重新进入新的准稳态。选取母线13、22、25、92、97、120、122、133、139的电压相角为系统输出，并在每个阶段中选取200 s的时间长度，分别对这3个阶段采用SSI方法对IOM的频率和阻尼进行估计，结果如表3所示，可见SSI方法不论对处理类噪声数据还是对处理故障后的暂态数据时，都能准确地估计出区间振荡的频率和阻尼。

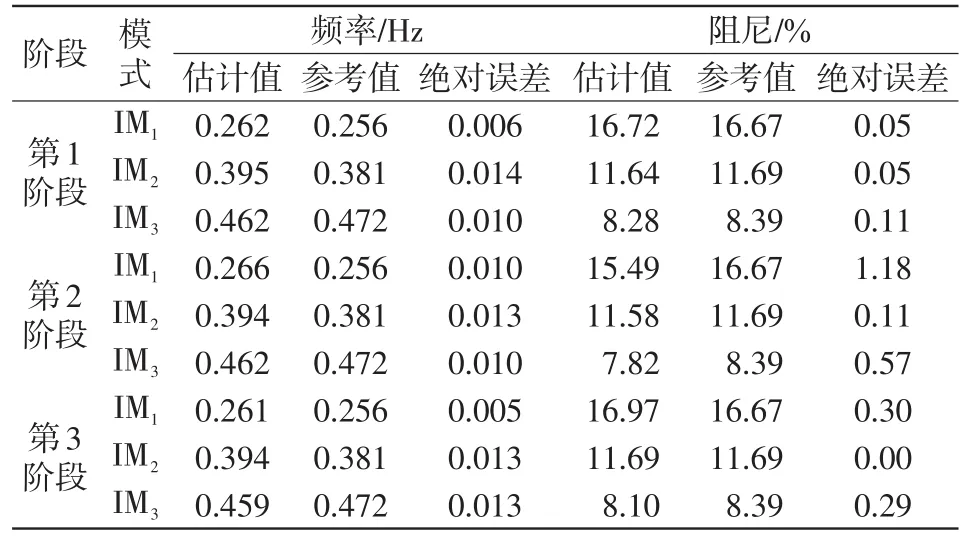
表3 NPCC 48机系统故障前后IOM估计结果Tab.3 IOM estimation results of NPCC 48-machine system before and after fault

然后，采用RSSI方法对于IOM进行在线估计，取前500 s数据为RSSI方法提供初始值，并对之后的1 000 s内每隔0.2 s的IOM进行估计，结果如图3所示。由图3可知，RSSI方法能同时准确地估计出3个模式的频率和阻尼。相比于其他估计方法，其具有快速准确地估计多个振荡模式的能力。

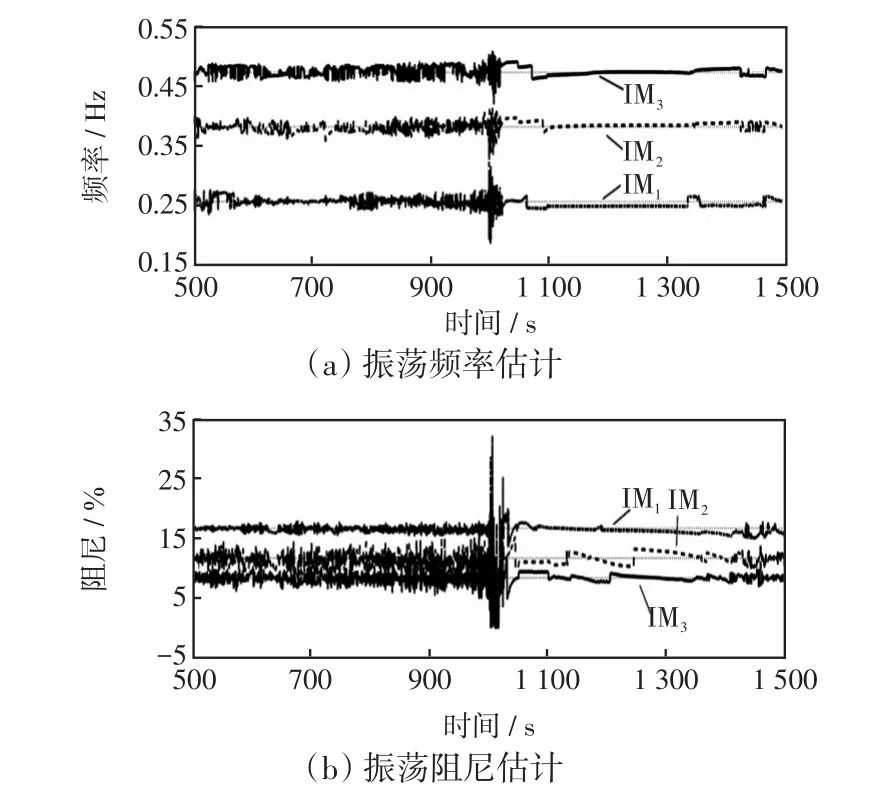
图3 NPCC48机系统部分3个IOM采用RSSI方法估计结果Fig.3 Three IOMs estimation results of NPCC 48-machine system via RSSI

4 结语

本文采用SSI方法在电网不同工况下，对IOM进行估计。同时，为克服一般SSI方法中奇异值分解计算量大的缺点，本文介绍了RSSI方法在电力系统区间振荡模式估计中的应用。仿真例子显示了这种方法的有效性，为以后多个振荡模式的准确跟踪提供了可能。