城市主干路系统开口分析与设计
王欣,范英飞,吕晏莹
城市主干路系统开口分析与设计
王欣1,范英飞1,吕晏莹2
(1. 西南交通大学,交通运输与物流学院,成都 610036;2. 沈阳理工大学,艺术设计学院,沈阳 110159)
本文主要研究城市主干路系统开口分析与设计。通过对现状主干路开口系统的描述, 基于Erlang分布模型对车辆进出开口的分析, 建立了目标路段内开口最短距离数学模型。通过对四川省自贡市街道的实例应用, 验证了模型开口距离设置的合理性。
城市主干路; 开口; 分析; 设计
0 引 言
近期,很多专家学者对快速路出入口设计进行了研究。其中,胡章立等[1]对城市快速路出入口的交通特性进行分类,并分析了各种形式出入口优缺点,对平行式出入口的设计提出相关的建议;童文聪等[2]采用道路空间利用、进出通道管理等技术对道路各类型典型开口进行比较分析,提出路段隔离开口的设计方法;谷莎、杨和平[3]从道路规划、绿化和交通工程三方面分析路侧交叉开口存在的问题,探讨从道路方案设计阶段就着手改变这种路侧设计不合理的方法,为有效预防或减少路侧交叉开口交通事故、维护交通安全提供参考;房琳[4]综合分析不同汇入控制形式下的车辆平均行程时间、通过交通量及平均延误。
随着城市的扩张,许多学校、商业中心等能够吸引大量车流量的大型公共建筑被规划在远离市中心的区域。这些大型公共建筑虽然远离市中心,但是考虑到吸引、方便顾客的因素,会被规划在主干路的两侧。查阅多地的《城乡规划管理技术规定》可知,各个地区对主干路两侧设置开口的规定并没有表示禁止、允许或者在何条件下允许,大多数城市规定:主干路两侧不宜开设机动车出入口,确需开设的,宜设置辅道和加减速车道,并应在区域路网和动态交通分析论证的基础上确定[5]。
鉴于相关的技术规定都没有明确主干路系统两侧开口设置的问题,本论文将主要讨论主干路两侧开口与上下游交叉口距离问题,并选取适当的方法和技术对问题进行讨论。
Erlang分布是描述车头时距较为常用的统计模型,可以根据模型中的取值而得到不同的分布函数。当=1时,Erlang分布可简化成负指数分布;当=30时,Erlang分布近似等于正态分布。可以描述行车流和拥挤车流的各种车流条件,的值越大说明车流越拥挤,驾驶员自由行车越受到限制,车流的随机性越差[6]。
很多专家学者利用Erlang分布研究了不同车流状态下车头时距的情况,裴玉龙、高晗[7]在总结、分析现有车头时距分布规律及Erlang分布函数特性的基础上,建立了快速路匝道连接段车辆车头时距分布模型,并指出对于高密度交通流Erlang分布描述效果具有明显优势;侯常明等[8]应用Erlang分布值分析高速公路隧道进出口车头时距分布规律;翟京等[9]研究城市不同类别道路的车头时距分布规律,采用Erlang分布拟合不同条件下的车头时距分布,并进行检验;易东波等[10]通过与正态分布情形下的相关结果比较,发现在Erlang分布需求下的最优动态批量策略效果要优于正态分布。
综上,本文讨论城市主干路开口分析与设计,利用Erlang分布模型,研究两种不同开口情形下目标路段内设置开口时应符合的最短距离要求。
1 预备知识
该部分将对一些必要的预备知识进行介绍。
1.1 Erlang分布
设目标车道的车头时距服从Erlang分布,根据数理统计知识可得密度函数[11]:

式中,为每条车道上的车流量(pcu/h);为车头时距(s);为分布函数参数,可以描述车流的拥挤程度,当=1时()为负指数分布,当时()为均匀分布;为自然对数。
在实际的应用中,的值可以由实际调查得到的均值和方差2表示,并四舍五入取整[11]:

1.2 汇入目标车道车辆等待平均距离
假设路段上有条车道,在开口路段下游交叉口因渠化新增的左转车道条。设社会车辆全部为小汽车,每条车道上的车流量为(单位:pcu/h,下同)。同时认为,在路段上社会车辆均匀分布。定义开口距上游交叉口的距离为L(m),开口距下游交叉口的距离为L(m)。
1.3 车辆临界车头空距平均值
当目标车道的车头时距大于目标车道的临界车头时距T时,车辆可以变道;当目标车道的头时距小于目标车道的临界车头时距T时,车辆不可变道[12]。
因此,小于目标车道的临界车头时距T的平均车头时距值为[12]
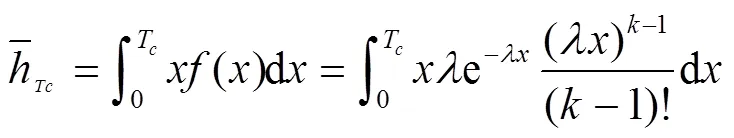
因此,小于临界车头时距的车头空距平均值为[12]:


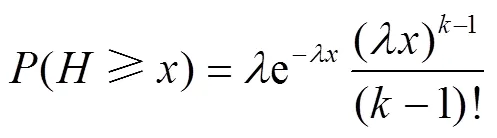
目标车道的任意一个间隔被拒绝的概率为:

设有连续个间隔被拒绝,第1个间隔接受车辆汇入目标车道,则车辆在等待个间隔之后,在第1个间隔接受车辆汇入目标车道的概率为[11]:

车辆平均等待的间隔数量可以表示为[12]:
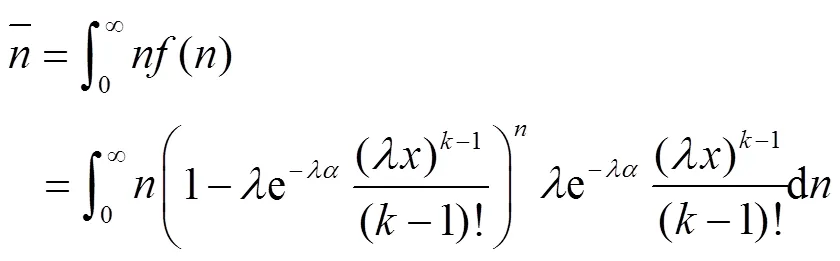
车辆在汇入目标车道之前需要等待的距 离为:
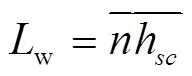
1.4 车辆变道过程行驶距离
若车辆在变道时横向移动的距离是1m/s,车道宽度为3m,则车辆在变道时行驶的距离为:

式中,为目标车辆行驶的速度(单位:m/s)。
1.5 辅助车道加减速段长度
本小节将讨论两种不同情形下的主干路两侧开口。
1.5.1 主干路两侧开口设置加减速车道
若车辆从车道汇入减速车道后,车辆速度减速至可进入开口的速度所行驶的距离为:

1.5.2 主干路两侧开口未设置减速车道

由于不设置加减速车道的情形是在最外侧车道完成加减速的,该种情况相比设置有辅助车道加减速段的情况少了一次变道,计算所得的距离必定小于设置有辅助车道加减速段的情况。
1.6 车辆停车距离
若车辆变道成功后开始减速至停车开始排队,则车辆在减速时行驶的距离为:
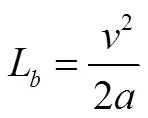
1.7 排队长度
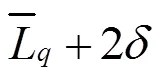
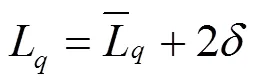
式中,L为下游交叉口平均排队长度;为调查数据的标准差。
2 模型的建立
该部分分别研究主干路车辆进入开口和车辆自开口进入主干路两种情况,并分别建立开口距离的模型。
2.1 车辆变道进入路侧出口
如图1所示,假设目标路段为双向8车道,车辆从道路交叉口进入研究路段后,如果车辆进入最右侧车道,则不需要经过变道,当车辆行驶到减速车道且符合变道的条件时,车辆直接汇入减速车道,车辆在减速车道速度降低到适合进入开口的值;如果车辆进入最左侧车道,则需要寻找合适的变道条件进行三次变道,当车辆行驶到减速车道附近时,寻找合适的汇入条件进入减速车道。
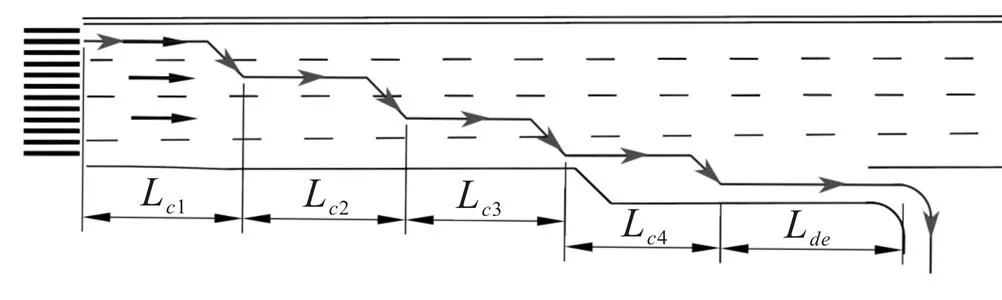
图1 车辆变道进入路侧出口示意图
因为要进入路侧出口的车辆在驶入该目标路段时占用哪一条车道是不能确定的,所以要考虑变道次数最多的情况,即假设有条车道,要考虑车辆变道-1次才能到达最外侧车道的情况。
因此,路侧出口距上游交叉口的最短距离可以表示为:

式中,L开口距上游交叉口的最小距离;L目标车辆完成一次变道行驶的距离;L目标车辆在减速车道上减速至可进入开口的速度的过程行驶距离。
2.2 车辆从路侧开口变道进入下游交叉口
如图2所示,假设目标路段为双向8车道,车辆从路侧开口变道进入下游交叉口时,如果车辆需要右转,进入最右侧车道,则不需要经过变道,当车辆在加速车道加速后且寻找到合适的变道的时机时,车辆直接从加速车道进入右转车道;如果车辆需要左转,则需要车辆在加速车道加速后且寻找到合适的变道的时机进入最右侧车道,并且寻找合适的变道条件进行三次变道,进入最左侧的左转车道。另外还要考虑车辆遇到路口红灯排队时,车辆刹车所使用的刹车距离,以及等待在道路交叉口前车辆的排队长度。

图2 车辆从路侧开口变道进入下游交叉口示意图
因为车辆从路侧出口驶入该目标路段的下游道路交叉口时,转向的意图是不能确定的,所以要考虑变道次数最多的情况,即假设有条单向车道,道路交叉口因渠化而新增的左转车道条数为,要考虑车辆变道+-1次才能到达最内侧车道的情况。
因此,路侧出口距下游交叉口的最短距离可以表示为:
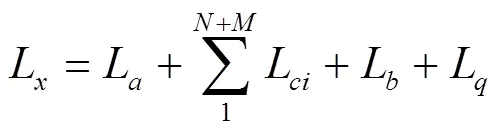
式中,目标车辆完成一次变道行驶的距离为L;目标车辆在加速车道上减速至可汇入行车道的速度的过程行驶距离为L;目标车辆在下游交叉口前排队停车时行驶距离为L;目标车辆在下游交叉口排队长度为L。
由公式(3)-(15)可以得到:
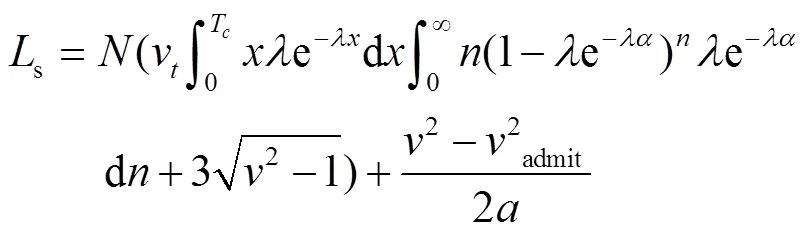

式中,为因渠化而增加的左转车道数量。
其中,加减速车道的距离为:
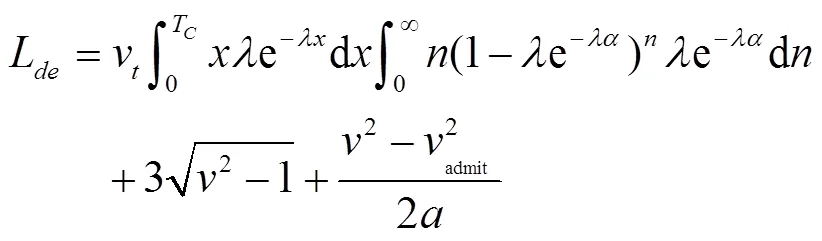

3 算例分析
以四川省自贡市丹桂大街、汇兴路为样本算例。丹桂大街属城市主干路,呈南北走向,北起于簸米湾隧道,南止于汇川路,全长约2.5 km,规划红线宽度40 m。用统计的方法得到100组道路交叉口各个车道排队长度的数据,并且经过统计分析得出其均值和标准差,如表1所示:
表1 调查路段交叉口排队长度均值及标准差

Tab.1 Mean and standard deviation of queue length at surveyed intersections
根据调查所得数据,利用公式(16)和(19),经MATLAB编程计算得到道路现状及开口距离理论值(见表2)。为了进一步分析道路开口设置的合理性,表3进行了理论开口距离与实际距离的比较。
表2 样本算例道路现状及开口距离理论值

Tab.2 Current status of the surveyed segment and computed value of the opening distance
表3 距下游交叉口距离理论值与实际值对比

Tab.3 Actual and computed value of the distance to the downstream intersection
分析可知,华医口腔医院、汇景苑两处开口的现状为:华医口腔医院出来的车辆右转进入丹桂大街,经过加速、变道等能够以较少的冲突通过下游交叉口;汇景苑汇入汇兴路的车辆离交叉口较近,经常出现强制变道的情况,并且在进入交叉口前与其他车辆冲突较严重。这与表3中计算结果得出结论相同。由于华医口腔医院处开口距离实际值大于理论值,故强制变道、交通冲突较少;汇景苑处开口实际距离小于理论值,故常出现强制变道行为。
4 结束语
本文研究了城市主干路系统开口分析与设计,通过相关的分析本文可以得出如下结论:
(1)辅助车道的长度与最外侧车道限速、开口限速有关,两者限速差越大辅助车道长度就需越长。
(2)主干道沿线开口距离与道路限速、下游交叉口排队长度、道路车头时距有关。
(3)建议主干路沿线新建开口应设置加速车道,进一步减少汇入主干道的车辆因车速差引起的交通冲突。
[1] 胡章立, 苏龙, 羊明. 城市快速路主路与辅路间出入口设计探讨[J]. 城市道桥与防洪, 2014(2): 24-26.
[2] 童文聪, 汪涛, 马万达. 城市郊区主干道路段开口设计方法[J]. 公路, 2010(11): 117-122.
[3] 谷莎, 杨和平. 浅谈基于道路交通安全的路侧交叉开口设计[J]. 湖南交通科技, 2014(3): 174-178.
[4] 房琳. 城市快速路入口设置优化研究[D]. 南京: 东南大学, 2016.
[5] Linying Liu《泸州市城乡规划管理技术规定》[EB/OL]. https: //wenku. baidu. com/view/1388dc3f580216fc 700afd 0a. html. 2012-02-01/2018-06-05
[6] 王殿海. 交通流理论[M]. 北京: 人民交通出版社, 2002.
[7] 裴玉龙, 高晗. 城市快速路匝道连接段车头时距分布模型[J]. 交通信息与安全, 2007, 25(5): 4-7.
[8] 侯常明, 郎海鹏, 张蕾. 高速公路隧道口车头时距分布研究[J]. 公路与汽运, 2009(6): 65-67.
[9] 翟京, 冷军强, 王天逸. 冰雪条件下城市道路路段车头时距[J]. 科学技术与工程, 2011, 11(5): 1131-1134.
[10] 易东波, 鲍玉昆. 基于爱尔朗分布的随机动态批量决策研究[J]. 武汉理工大学学报: 信息与管理工程版, 2012, 34(1): 87-92.
[11] 何平. 数理统计与多元统计[M]. 成都: 西南交通大学出版社, 2004.
[12] 王京元. 信号交叉口时空资源综合优化实用方法研究[D]. 南京: 东南大学, 2006.
(中文编辑:刘娉婷,英文审改:杨鸿泰)
Analysis and Design of Access of Urban Arterial Roads
WANG Xin1,FAN Ying-fei1,LV Yan-ying2
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China; 2. Art and Design College, Shenyang Ligong University, Shenyang 110159, China)
This paper aims to analyze and design the access of urban arterial roads.Based on the description of the urban arterial road system, a mathematical model is constructed to describe the minimum distance between the in tersection and access along the target road. By applying the model to the streets of Zigong in Sichuan province,validity of the model is verified.
urban arterial road; access; analysis; design
1672-4747(2018)03-0098-06
L1491, 2+3
A
10.3969/j.issn.1672-4747.2018.03.014
2017-03-30
王欣(1991—),男,河南人,西南交通大学硕士研究生,研究方向:交通运输系统工程。
王欣,范英飞,吕晏莹. 城市主干路系统开口分析与设计[J]. 交通运输工程与信息学报, 2018, 16(3): 98-102, 118.

