基于PCA-LVQ的专业可持续发展综合分类研究

谢颖 朱远胜 姚雪存 马维聪

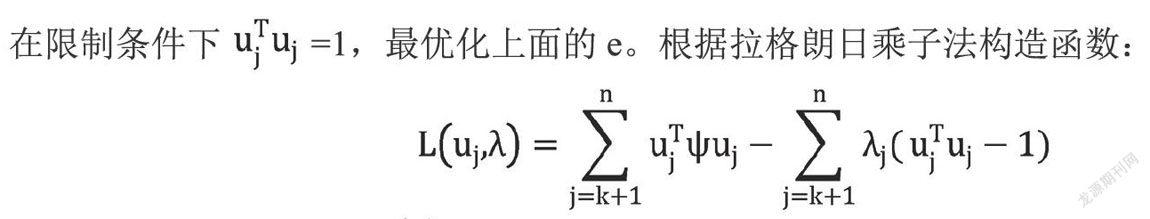
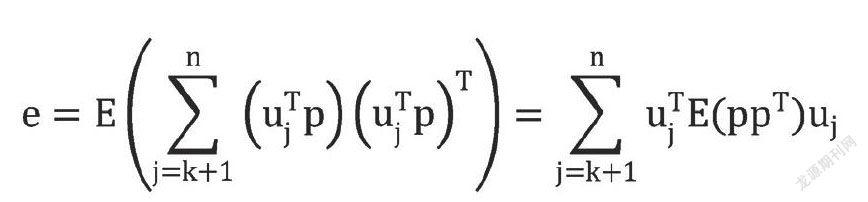
摘 要：提出将PCA及LVQ网络用于专业可持续发展分类应用研究，通过多种调研形式获取专业发展的21项指标，首先对比使用标准正交归一化方法和min-max归一化方法对原始的样本进行归一化，再利用PCA算法解除样本特征的相关性，实现数据的降维。最后利用LVQ神经网络对已经降维的数据进行学习，并得到学习结果，最后利用学习得到的权值矩阵对新的样本进行识别，判断专业发展水平。

关键词：主成分分析;学习矢量量化网络;专业可持续发展

中图分类号：G434             文献标识码：A             文章编号：1674-2346（2018）04-0084-08

如何评价专业发展水平是专业发展过程中的重要问题，根据相关文献总结各类院校在进行专业发展过程中提出和实施的各种措施，用指标的形式加以固化，进而通过专家评审、调查问卷、现场调查、参考相关调查结果等形式对专业发展的各项指标进行量化。以浙江省高职类院校省级示范专业和优势专业作为合格类样本库，以其它专业作为不合格类样本库，对比使用min-max、标准正交化2种方法完成数据规约，消除数据量纲不同导致的数据差异，接着用PCA对各类样本的指标进行“解耦”，消除不同数据特征之间的线性相关性，获取相互不相关的新的指标集，最后利用LVQ网络对这些新的指标集样本进行学习，通过学习得到专业发展水平高低的判别模型，从而为指导专业可持续发展提供识别标准和改进依据。

1    建立评价指标体系

专业可持续发展总体上可以分为：专业规划、专业实施与保障、专业产出与评价3个方面，[1]而从更加细致的角度来看主要分成5个方面：1）师资队伍建设是学科专业建设的关键。[2]构建具有前瞻性眼光、高深造诣的专业带头人队伍，在他们带领下建设一支知识结构广博、年龄结构和职称结构合理、学术水平精深的师资队伍是专业可持续发展的人才保证。[3]2）教材体系建设是专业可持续发展的载体。构建知识融会贯通，专业和培养方向明确、模块结构合理的教材体系是专业可持续发展的物质基础。3）课程改革与实践是专业可持续发展的保证。课程改革与实践的对象包括课程改革与实践的主体对象――老师和学生，同时也包括客体对象如：科研成果、教改成果、社会服务成果、学生技能培训成果等。4）信息化建设是专业实施过程中的灵魂。围绕专业发展的信息化建设，包括资源库建设、精品课程建设、网络课程建设、视频教程建设、顶岗实习平台建设、培养方案建设、培养计划建设等等。这些信息系统的建设一方面为专业实施提供合理的手段，也是知识、能力传承的重要载体，合理的教学信息系统的构成能为专业实施提供强大的支撑，也为专业实施指明方向。5）实验实训场地与基地建设是专业发展的根据与桥梁。它对改善课程设置、提高人才培养质量、更好的服务当地经济社会发展，具有重要作用。[4]

综上所述，将专业可持续发展指标以列表形式总结，如表 1所示：

2    相关理论基础

2.1    PCA算法理论

PCA（Principal Component Analysis）中文名--主成分分析。PCA是投影平方最大化、误差最小化的一种算法，是模式识别中常见的线性映射方法，由于PCA算法在降维和特征提取方面的高效性，在模式识别领域也得到了广泛的应用。其核心思想是将高维空间中的向量，通过矩阵转换为低维空间的向量，在尽量保持原有数据信息的基础上消除高維空间向量特征的线性相关性，这样对于后继的神经网络来说，可以减少训练时间，提高训练效率，增强网络的泛化能力。[5]PCA在信号处理、图像分析领域也有广泛的应用。PCA算法基础是K-L变换，当样本中心化以后，K-L变换就变成了PCA。[6]

离散K-L变换：

它是一种基于目标统计特性的最佳正交变换，任意n维随机向量 （一个样本可以看成是一个随机向量的实现），存在n维标准正交变换矩阵，其中 ，使得样本p是这个标准正交基的线性组合，记为：

两边同时乘以       ，并考虑正交基特性得到：

现在假设用前k项（1≤k则均方误差为：

将（1）式代入得到：

令                      ，则截断误差可以简记为：

在限制条件下          =1，最优化上面的e。根据拉格朗日乘子法构造函数：

求偏导令其等于0，即                   得到：

即满足上式时，e取最小值。此时E（xxT）为自相关矩阵， j为自相关矩阵的特征值，uj为特征值 j对应的特征向量。将（3）式代入（2）式，得到：

因此，将自相关矩阵的特征值由大到小排列，特征值对应的特征向量正交，且取前面k个向量构成了转换矩阵 ，截断误差是后面从k+1开始到n的n-k个特征值的和。

当向量x中心化以后，上面的自相关矩阵就是协方差矩阵（忽略系数），此时就是我们所说的PCA算法，理论已经证明，虽然构成向量x的基有无穷多个，但是，标准正交基下的截断误差最小。

2.2    LVQ神经网络理论

学习矢量量化网络（Learning Vector Quantization简称LVQ）是一种自适应数据分类混合网络，是用数学方法对神经系统的横向抑制功能的模拟，通过将有监督和无监督学习结合起来提高网络对输入向量分类的正确性。[7]

LVQ神经网络由3层神经元构成，即输入层、隐含层（竞争层）和输出层（线性层）[8]，其基本结构如图1所示。LVQ网络的输入层和隐藏层之间为全连接，而隐藏层和输出层之间为部分连接。[9]输入层和竞争层之间是无导师学习，某个神经元通过竞争及对其它神经元的抑制而获胜输出为1，其它神经元输出为0，隐藏层和输出层之间为有导师学习，主要完成逻辑“与”的功能，将获胜神经元指派给某个类别。

2.3    LVQ训练规则

1）有m个输入向量，                                              与隐含层神经元之间的权值向量为iW  ，上标1表示第1层（隐含层）到竞争层的权值，所以共计为m个权值向量（列向量），记为1W ，2W  ，…，mW  。初始值取比较小的随机值。

2）设置                                     子类i是k类的一部分，其它都为0，也就是说如果pi属于类k，那么                。

3）随机抽取的样本pj输入网络，按照如下公式求其输出。

n1直接计算权值向量和输入向量的距离，并通过竞争，得到a1（只有1个神经元获胜，结果为1，其它都为0），然后a1与导师向量权值矩阵W2相乘，得到类别结果。根据结果对jW1进行调整，因为输入的向量是pj，而pj对应的权值为jW ，所以调整的是jW 。

4）更新权值，采用kohonen规则进行更新。如果在a2的输出中，pj被正确的分类了，那么，要使得jW  向pj靠拢即：

为学习速度和遗忘速度，这里取二者相等。

如果在a2的输出中，pj没有被正确的分类，那么就应该使得jW  遠离pj，此时调整公式为：

然后依次循环输入各个样本向量。

5）判断是否收敛。常见的判断收敛方法有2种：第1种判断迭代次数是否达到预设的最大值，若没有达到最大迭代次数，则转到第3步，否则训练结束;第2种则是在实际项目中，通过判断MSE均方误差作为循环终止条件，即前后2次计算输入层和隐含层之间的权值矩阵的均方误差，只要不大于某个阈值就可以终止迭代。Matlab则是将这2种方法同时使用，无论哪个先达到条件，就终止迭代。

3    基于PCA-LVQ模型的建立

3.1    数据来源及样本集

依据如表 1所示21项指标，通过专家评审、调查问卷、现场调查、参考相关调查结果等形式对专业发展的各项指标进行量化，得到如下数据表（表2）。

3.2    构建PCA-LVQ网络模型新的评价样本集

在采用PCA算法对原始样本进行转换之前，为消除数据量纲不同导致的数据差异，对比使用min-max和标准正交化2种方法完成数据规约，2种方法规约后调用matlab的princomp函数完成PCA转换后的特征值及贡献度如表3所示，为了方便显示最终结果，在源数据中将优势专业和示范专业的3个样本分别放在1，2，3位置。PCA执行结果如表3所示。

从表3中可以看出：min-max归一化后的PCA分析结果表明，前9项特征值贡献度为93.48%;标准正交化归一化后的PAC的前9项特征值贡献度为93.37%。二者基本相同，即前9项可以代表原样本中的93%左右的信息，后面LVQ的处理就基于前9项数值进行神经网络学习。

PCA降维后的转换矩阵及新的样本集说明如下。

PCA转换后主要关注3个方面的内容：1）归一化时计算的均值、方差或min以及max值，对于“行”是样本，“列”是特征来说，这些值都是针对“列”而言，这些值是后继规约化识别样本要用到的数据。2）根据特征值贡献度选择相应的特征向量构成的转换矩阵，因为前面选择了前面9个特征值，所以，转换矩阵选择由前面9个向量构成的矩阵，这样，原来21维的样本就降维为9维数据样本，这些样本能反应原来样本的约93%的信息。3）原来样本在新的基空间中的向量矩阵，这是后继LVQ的输入向量。

3.3    PCA-LVQ网络模型的参数设置

LVQ神经网络的输入层为17个神经元，因为这里初始训练样本个数为17，输出层2个神经元，代表2个类别，输入层每个样本有9个向量，决定了输入层到隐藏层的权值矩阵是17？，隐藏层到输出层的权值矩阵为2？7，隐藏层与输出层的权值矩阵在学习前由导师数据的类型设置如下：

前3列的第1项为1，第2项为0，后面14项的第1项为0，第2项为1，表示前3个样本是同一种类别（代表优势专业和示范专业类别），后面14个样本为第二种类别（非优势专业和非示范专业）。这个设置过程实际代表了导师样本的分类学习。训练的迭代次数设置为1000，最小均方误差MSE设置为0，训练过程中先到者为准。

4    网络模型的训练与识别

4.1    对比minmax及标准正交化的训练结果

LVQ神经网络结构如图2所示。

训练结束时的迭代次数与均方误差如图3及图4所示：

在试验中，尽管每次迭代次数可能都不相同，但是，通过多次试验可以发现，从总体上，标准正交化后的数据进行LVQ分类学习时的迭代次数大概在20左右，此时的MSE达到了0，也就是说对于学习数据的分类完全符合要求。而min-max的LVQ神经网络学习次数在10次左右，所以，仅仅就学习的收敛速度而言，min-max的学习速度要快于标准正交方式。min-max的性能是标准正交化方式的2倍左右。并且最终都学到了100%的分类能力，两者都能正确的对导师数据进行分类，如所示：

图5说明对17个导师样本进行了学习，前面已经说过，前3个样本是合格类样本，后面14个样本是非合格类样本，系统最终能完全将2类数据分开。但是2种方法所获取的权值矩阵不一样，最终将会展示完全不同的识别能力。试验中使用的是matlab2014b软件，这个软件版本没有像以前版本那样自动对数据进行训练、校验和测试的比例分配，直接将所有数据作为训练数据。

4.2    识别

用23个样本进行识别，在设计样本识别过程中，将训练用的17个源样本加入，新添6个新样本，其中倒数第2个样本为合格类样本，其它5条为不合格样本，这里要注意，对识别的原始样本进行标准正交化和min-max规格化的时候，使用的均值、方差、min值和max值是训练样本中的值，不能用识别样本中的相关值，采用sim方法进行仿真（识别）。得到的结果如表4所示（结果采用了matlab的vec2ind转换并对结果进行了转置）。

上述数据表明，在专业可持续发展分类研究项目中，标准正交化归一法得到的最终识别率为100%，而通过min-max规约后的神经网络的识别能力只有60.8%，前者远远高于后者的识别能力，造成这种识别能力巨大差异的主要原因在于待识别的样本基本按照正态分布，而标准正交化归一法的一个隐含的前提就是数据如果基本符合正态分布，那么识别率是非常高的，不过准确率一般来说是达不到100%的，这可能只是一个巧合而已，另外，样本数目不多，也是一个很重要的原因。反之，如果样本不符合正态分布，那么标准正交化归一法后的LVQ识别率也不会非常高，这是实际项目中应该注意的问题。

4.3    总结

LVQ作为一种集监督和无监督学习为一体的神经网络，理论上对样本没有提出归一化要求，其分类或者说聚类能力是比较强的，但是有相关文献已经证明当样本特征存在较强关联性时，LVQ的功能不能得到有效发挥，因此，PCA作为一种降维和特种提取算法，刚好是对LVQ神经网络的一种有益补充，二者相得益彰。同时，在处理类似问题时，样本特征的选取是非常重要的，好的样本属性确实能反应样本的本质特征，通过学习获得的识别能力就非常强大;反之，则识别能力就很弱。

另外，从以上数据获取、规约数据、PCA降维、LVQ分类和识别过程的结果可以得出结论：专业可持续发展的21项指标的建立是比较符合实际分类标准的，按照21项标准采集的数据经过标准正交化数据规约后，通过PCA消除特征的相关性，再经过LVQ网络的识别，能够学习到用于识别的权值矩阵，依据这些权值矩阵和正交化过程中获取的均值和方差就能够以很高的识别率判断专业的发展水平。权值矩阵、均值和方差、转换矩阵構成了依据21项指标判断专业发展水平的模型。

参考文献

[1]夏淑华.高职院校专业可持续性发展思路及实施措施研究[J].学理论，2015（30）：174-175.

[2]黄海，王竹立.中山医科大学教学资源库的构建与实现[J].中国医学教育技术，2002，16（3）：162-165.

[3]严珍珍，蒋志芳.信息与计算机科学专业可持续发展的探索与实践[J].高师理科学刊，2014，34（2）：82-85.

[4]钟耀平.地方本科院校商务英语专业课程设置调查和分析[J].宁波工程学院学报，2017，29（1）：122-127.

[5]谭莉，于春梅.基于PCA_LVQ神经网络的化工过程故障诊断[J].工业控制计算机，2016，29（11）：86-87.

[6]谢建龙，汪亚明.基于PCA算法的运动员动作识别技术研究[J].工业控制计算机，2014，27（4）：138-139.

[7]王民.基于LVQ神经网络的朱鹮个体辨识技术研究[J].信息通信，2015（9）：7-8.

[8]赵学观，王秀，李翠玲，等.基于主成分分析及LVQ神经网络的番茄种子品种识别[J].浙江农业学报，2016（8）：1379-1380.

[9]谢丽蓉，王晋瑞.基于LVQ_GA_BP神经网络的煤矿瓦斯涌出量预测[J].煤矿安全，2017，48（12）：154-156.

Study on Comprehensive Classification of the Sustainable Development ofProfession

Based on PCA-LVQ

XIE Ying   ZHU Yuan-sheng   YAO Xue-cun   MA Wei-cong

（Teaching Affairs Office，Zhejiang Fashion Institute of Technology， Ningbo，Zhejiang 315211，China）

Abstract： In this paper，PCA-LVQ networks are applied to the classification and application ofthe sustainable development of profession and 21 indexes of professional development are obtained through various investigation forms.First，the standard orthogonal normalization method and the min-max normalization method are compared to normalize the original samples.Then the PCA algorithm is used to remove the correlation of the sample features and to reduce the dimension of thedata.Finally，LVQ neural network is used to study the dimension reduced data and the learning result is obtained.The weight matrix is used to identify the new samples and judge the level of professional development.

Key words： principal component analysis;learning vector quantization network;sustainable development of profession