经历建模过程 感悟方程思想
——《列两步计算方程解决实际问题》的思考与实践
江苏扬州市甘泉小学 钱 燕
案例背景:
方程作为一种重要的数学思想方法,对丰富学生解决问题的策略,突破算术思维方法的某些局限性,提高解决问题的能力,发展数学素养有着非常重要的意义,也为学生今后进一步学习代数知识以及其他学科知识奠定了重要基础。基于《义务教育数学课程标准(2011年版)》修订后的苏教版数学五年级下册关于方程这一单元的知识有了较大幅度的增加:原五年级下册只要求学生解一步计算的方程,并列一步计算的方程解决简单的实际问题,稍复杂的两、三步计算的方程及其应用则安排在六年级上册。现在这些内容经过整合,集中安排在五年级下册第一单元。
我区针对修订后的教材变化较大的部分内容,开展了区“幸福课堂”教学竞赛活动,笔者有幸执教了《列两步计算方程解决实际问题》这节课,经过一次次的试教、修改、失败、再探索……笔者若有所悟,对这节课有了更多的思考和认识。
我的思考:
1.教材为什么要整合
小学生对方程的认识主要包括方程的含义、解简易方程和列方程解决一些实际问题。实验教材是分散安排的:第一次安排在五年级下册,第二次安排在六年级上册,修订教材将这些内容经过整合集中安排,主要出于以下两点考虑:一是由于上述一步计算的方程到两、三步计算的方程,尽管形式上稍复杂一些,但解方程的原理和步骤并无明显差异;二是因为绝大多数五年级学生对一步计算的实际问题都比较熟悉,让学生在一个阶段只学习用一步计算的方程解决实际问题,挑战性略显不足,不利于学生保持对方程内容的好奇心以及探索方程解法的积极心态,也不利于学生充分感受方程思想的特点和价值。
2.如何建构方程思想
方程刻画的是现实世界中的等量关系。学生在小学阶段的数学学习中习惯了用算术方法解决实际问题,而列方程解决实际问题则是学生思维方式的一次重要转折。本节课的教学中,需要让学生通过寻找数量之间的相等关系,并借助含有未知数的等式进行表示,在经历抽象、建模的过程中感悟“方程”思想。这个过程实际上就是让学生经历数学化的过程,突出数学的本原,从而促进学生应用数学知识解决实际问题能力的提高。
我的实践:
带着这样的思考,我进行了第一次试教,按照创设情境,导入新课—抓住关键句,分析数量关系—引导学生列方程—学习解方程—检验、回顾反思这几个步骤来进行教学,结果发现,学生学习的主动性没有被激发,只是机械地模仿列方程,至于为什么要列方程?选择哪个等量关系式列方程?列方程有什么好处?大部分学生一片茫然。但此时笔者心中的思路似乎更明晰了,觉得应着重从“抓住关键句进行数量关系分析,列出符合题意的方程”和“将方程方法与算术方法巧妙地进行对比,明晰解题思路”两方面入手。现撷取几个精彩片段与大家分享:
一、前移数量关系分析,提高学生的分析能力
用方程解决生活中的问题,关键在于让学生能正确寻找问题中的数量关系,理解了数量关系,问题便迎刃而解。所谓“磨刀不误砍柴工”,笔者将数量关系的分析前移至课始,始终把数量关系的训练作为教学的主线贯穿在教学过程中,并对教材进行创造性的处理,从学生感兴趣的比年龄和身高这一生活经验开始,由易到难,循序渐进地夯实数量关系的训练,分三个层次进行。
1.比年龄(倍数关系)
师谈话:谁呀?(钱老师)认识吗?(周雨)我校的小歌星。
出示:钱老师的年龄正好是周雨的3倍。
提问:你能想到什么等量关系?
生:周雨的年龄×3=钱老师的年龄。
2.比身高(相差关系)
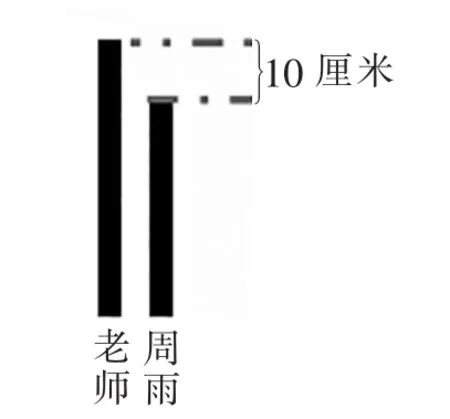
(师出示图)提问:根据这幅图,你能说出哪些等量关系式?
生1:周雨的身高+10厘米=老师的身高。
生2:老师的身高-周雨的身高=10厘米。
生3:老师的身高-10厘米=周雨的身高。
有了这个简单的示意图,学生很容易地说出了3个等量关系式,从图上清楚地看出钱老师的身高比周雨高10厘米,也就是周雨的身高比钱老师矮10厘米。
3.比身高(稍复杂关系)
姚明的身高比周雨身高的2倍少74厘米。
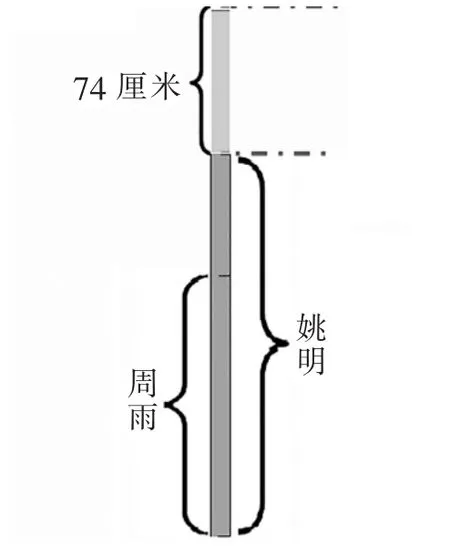
(出示图片:姚明、周雨)提问:他们俩身高的关系想知道吗?出示:姚明的身高比周雨身高的2倍少74厘米。
师示范读:挺复杂的,你们懂吗?
谈话:钱老师有点不懂,少74厘米,难道姚明比周雨还要矮呀?
生(反驳):不是、不是,是比周雨身高的2倍矮,课件上文字放大变色:“周雨身高的2倍”。
提问:你关注到了姚明的身高是跟周雨身高的2倍比的。周雨身高的2倍在哪呢?
学生上台指,并结合课件进行动画演示。
师:你的意思是说,一个周雨的身高再摞一个周雨的身高,2个周雨的身高少74厘米就是姚明的身高。(多媒体动画演示)现在,你能找出等量关系吗?
生1:周雨的身高×2-74厘米=姚明的身高。
生2:周雨的身高×2-姚明的身高=74厘米。
生3:周雨的身高×2=姚明的身高+74厘米。
这里的数量关系要比前面两题复杂许多,但因为有了前面的铺垫,此处只需明确姚明的身高是与“周雨身高的2倍”比的,然后再通过多媒体课件进行形象直观的动画演示,学生真正理解了这句话的意思,就能很快地说出三个不同的等量关系式。
二、依据数量关系列出方程,自主探究方程的解法
《义务教育数学课程标准 (2011年版)》指出:“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展。”数学教学应最大限度地满足每一个学生的需要,最大限度地开启每一个学生的智慧潜能。本节课的重点应是让学生依据数量关系式列出符合题意的方程。于是,我巧妙地将顺向思维与逆向思维进行初次对比。
提问:现在,你们最想知道谁的身高?
生1:我想知道周雨的身高。
生2:我想知道姚明的身高。
师:如果老师只想告诉你周雨的身高是150厘米,有办法求出姚明的身高吗?
生:150×2-74=226(厘米)。
师:如果反过来,知道姚明的身高,求周雨的身高,你们会吗?(课件出示:完整的题目)

学生看到课件中的等量关系式,异口同声地说出:可以列方程解决。(板贴课题:列方程解决实际问题)
接下来,让学生自主列出方程,自主探索出解方程的方法,并学会检验。最后,再帮助学生总结出列方程解决两步实际问题的一般步骤:抓住关键句,找最容易想到的等量关系式、然后列方程、接着解方程、最后检验。
提问:哪一步最关键?
生齐答:根据关键句找最容易想到的等量关系式这一步是最关键的。
有了前面的铺垫,学生解决这道例题时就会得心应手,回想起自己一开始试教时,将题目整体呈现在学生面前,学生真有斗大馒头无从下口之感,也让学生的自信心倍受打击,学习效果当然就差。因此教师在教学过程中,要关注学生在数学活动中所表现出来的情感与态度,帮助学生认识自我,建立信心。良好的数学情感与态度是学生参与数学活动的重要动力,是克服困难和探索创新的力量源泉。
三、巧妙对比明晰思路,提升学生的思维能力
教育的目的之一就是引发学生思维的碰撞,并且引导学生深入思考,开拓思维。本节课的主要学习内容是《列方程解决两步实际问题》,为了克服学生的思维定式,也为了让学生真正理解什么时候该用方程解,什么时候用算术方法解,在巩固练习阶段我设计了一系列的闯关游戏,让学生在一次次的挑战中进一步明晰解题思路,提升学生的思维能力。

学校体育室有若干排球和篮球,排球有18个,篮球的个数比排球的3倍少6个,篮球有多少个?
排球的个数×3-6=篮球的个数
解:设篮球有x个。
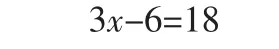
师出示上图:这题还不简单?今天学习的列方程解决实际问题,肯定用方程解,同桌互看一下(点击答案),和我不一样的起立,全班5人算错,这么简单的题目,你们还错啊?
站着的几个同学有意见了,说这题的等量关系式是:排球的个数×3-6=篮球的个数(点击出示等量关系)。现在排球的个数已经知道了,直接列算式算就可以了。
师:这几个同学真棒,他们能先找出等量关系,再根据等量关系发现排球的个数已经知道,直接用18×3-6就能算出篮球的个数,思路很清晰,坐着的同学听懂了吗?
数学课堂的学习始终都应该充满挑战性,学生获得数学知识本来就应该是在不断的探索中进行的,在这个过程中,学生的思维方法是各不相同的,很多时候一节课就只学习一个知识点,有不少同学就会依葫芦画瓢,机械模仿做题。为了克服这种思维定式,让学生跳一跳才能摘到桃子,笔者在课堂巩固练习环节,多次采用“上当教学法”,让学生进一步明晰思路:同样的等量关系式,如果知道排球的个数,就直接列算式解答;如果排球的个数不知道,就需要用方程来解决。巧妙的对比,对学生的思维更有冲击力,更有助于学生思维的提升。筻

