“三辨”方程，让认识直抵本质——《认识方程》一课的实践和思考

江苏南通市通州区实验小学 李红霞

备课时，有老师说，这堂课很简单，学生自学就能解决，不就是理解“含有未知数的等式叫方程”吗？

是的，本课的教学目标就是认识方程，那到底理解些什么呢？理解到什么程度？我回顾了以往学生的错误点，查阅了资料，看了顾亚龙老师的视频课，带着一份学习之心与学生一起找寻方程的庐山真面目。

通过天平图，学生们认识了方程和等式，并分析了方程和等式的关系，每人举3个方程的例子。（选取有代表性的例子，让学生板演）

①形如100-50=x是方程吗？

师：这些方程，能给他们分分类吗？

生1：我分两类，一类是含有加减法的方程；另一类是含有乘除法的方程。

生2：我也分两类，我是看未知数位置的，把未知数在等号前面的分一类，在等号后面的分一类。（板书如图）

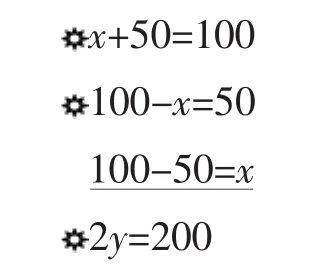
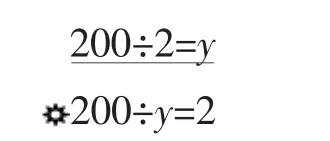
师：你觉得把未知数放在结果的位置上，好不好?为什么？

生：不太好。因为本来就可以直接算了，还加个未知数，感觉有些画蛇添足。

师：说得好。像这样的方程对解决问题没有帮助，不妨称为“坏”方程。其他方程中的未知数都参与解决了问题，不妨称为“好”方程。我们列方程尽可能列“好”方程。

②x=5是方程吗？

师:关于方程，你还有什么质疑吗？

生1：老师，我看到妈妈买的资料上有道判断题：x=5是方程。这对吗？

大家讨论。

生2：我觉得应该是的，因为它含有未知数，也是一个等式。

一部分学生点头默认。

生3：可是它看起来有点别扭，总觉得都已经知道x等于几了，没什么用。

生4：这就相当于天平左边是一块饼干，右边是一个5克的砝码。直接可以看出饼干重5克。

师：也就是说，这里的未知数没有参加计算。那这是方程吗？

生：我觉得这虽然是方程，但不是个“好”方程，它最好代表方程的解。

师：真棒，大家对方程的认识更进了一步。

③16-□=5是方程吗？桃树的棵数+50=100是方程吗？

师：学到这里，大家对方程已经很熟悉了。那老师考考大家，160-□=50是方程吗？

生（异口同声）：不是。

停顿片刻，有学生嘀咕：好像不一定?

师：这样吧，小组内把各自的想法或疑惑说一说，看看谁想的有道理。

（学生交流想法）

生1：我们组觉得不是方程，因为这和方程的样子不像，没有字母。

生2：我反对他的想法。我觉得字母可以表示未知数，方框也可以表示未知数。所以这个是方程。

生3：我也同意这个是方程。方程是含有未知数的等式，只要有未知数就可以了，不是只看字母。

生4：对的，方程可不是含有字母的等式呀。

师：把掌声送给认真思考的同学们。大家抓住了方程的本质——含有未知数的等式，就能正确判断了。看到这个例子，大家是不是觉得很熟悉，就是一年级时做的“在方框里填数”，这就是方程的雏形哦。看来，方程是我们的老朋友了。

生：老师，那方框也可以用图形来表示吗？我的意思是说以前做的16-★=5也是方程的雏形吗？

师：是的。在数学学习时，一开始我们接触的是填数或者用图形代表数，随着你们抽象能力的提高，学了用字母表示数，我们就把它抽象成字母，成了现在的方程。其实，方程的形成经历了悠久的历史。在很长一段时期内，方程没有专门的表达形式，而是使用一般的语言文字来叙述。直到300多年前，法国的数学家笛卡尔第一个提倡用x，y，z等字母来表示未知数，才形成了现在的方程。

师：所以，像“桃树的棵数+50=100”……

生1:也是方程的雏形。

生2：老师，方程应该就是表示已知和未知的相等关系。

（根据学生的回答板书：

相等

方程未知——已知）

关系

思考:

方程这个内容已经教过好几届，每次教总觉得看似简单，但是学生学得不透，不能真正建模，从而在解题时存在一定的问题。

1.能顺利辨认方程的样子就认识了方程吗

从概念看，方程是含有未知数的等式。但有些“形”是方程，却没有解决问题的价值；有些“形”非方程，却能体现方程的“神”：用已知和未知之间的等量关系来解决问题。

大数据时代让我们的学生们总是带着很多信息走进课堂。说到方程，他们并不陌生。但事实上，他们关注的是方程的直观表象：有字母，有等号。但对于方程的本质是未知的。因此，我们不能把这朦胧的感知作为已知，而是应该从他们已有的认识出发，指引他们关注方程的本质元素，找到方程的“形”和“神”。

2.能流利说出方程的定义就理解了方程的思想吗

“100-50=x”“x=5”形式符合方程的概念，但实质上并没有参加计算，没有解决问题的价值。在教方程时，我们常常困扰：学生总喜欢写成未知数在结果位置的样子。尽管一再强调这样写不太好，但依然有人如此，乃至后面列方程解决问题时也留有这样的“后遗症”。究其原因，学生只接受老师告知的“不太好”，而根本不知其真正的道理，所以并没有从内心去接受这样的要求。本课，我引导学生比较未知数在等号前和在结果的位置上，分别有什么不同？对解决问题有没有起到作用？从而让学生体验到，虽然这样的例子符合方程的概念，但对于解题并没有实质性帮助，正如学生所说“本来就可以直接算了，还加个未知数，感觉有些画蛇添足”。这样的深度理解，最终的效果是课后练习时没有一个学生愿意写这样的“坏方程”。

3.如何真正走进方程，正确建模

学到这，学生似乎已经把方程学得很透了，但事实上并没有真正建模。循着方程的发展历史看，早在3600年前埃及人就用方程解决问题了，中国人在2000多年前就在《九章算术》中用算筹来解决方程问题。所以，方程是用来表示已知和未知的相等关系，从而解决问题。至于字母，只是对未知数的一种简洁约定的表现形式。所以，我们对于方程的建模应该投射到“未知数”上。

形如 “16-□=5”“桃树的棵数+50=100”形式上不同于用字母表示的方程，但却体现方程的本质：表示已知和未知的相等关系。所以，联系低年级的填方框，图形代表几，再到现在用字母表示的形式，理解用不同形式表示未知数，层层深入，让学生真正实现方程的建模。

透过方程的“形”，抓住方程的“神”，才能真正认识方程。通过本课的思考、学习、实践、摸索，我深深地认识到，根据学生的盲点和知识的发展出发，全心地备一堂课，让学生学透、研深，才能实现课堂知识有效和超越。筻