架空输电线路地线多点取能的功率分布特性

谢彦斌,唐 杰,林 立,尹伟华,彭志华,文亚环

(1．邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422000； 2．邵阳学院 图书馆，湖南 邵阳，422000)

智能电网的建设和发展，离不开输电线路在线监测的应用和发展。由于输电线路比较长，一条输电线路通常需要多个监测点才能实现比较全面的监测，相应地也需要从多个监测点取能供电。受经济、技术条件的限制，输电线路在线监测装置的供电宜采用在线取能的方式[1-2],目前在线取能主要有利用太阳能或感应线圈从高压导线取能两种方式，这些方式存在输出功率小、装置体积大及绝缘等问题，无法充分满足在线监测装置的供电需求[3-7]。

输电线路运行时其周围存在电磁场，该电磁场来源于导线电荷的库仑电场和导线电流的磁场，因此可以考虑从架空地线抽取能量[8-13]，避免利用太阳能电池或从高压侧取电的弊端。研究表明[1-2]，地线取能功率通常比较小，地线取能可行与否的关键之一在于取能功率是否足够，因此对于多点取能的情况，有必要分析各取能点的功率分布情况，为在线监测及取能工程提供参考。

目前关于架空地线电磁取能的研究鲜见报道。文献[12-13]针对两地线均逐塔接地的架空线路，通过对一定范围内的地线采取绝缘化措施实现了较大的取能功率。其中前者是由绝缘化的两地线构成取能回路，后者则将多匝式电流互感器(current transformer，CT)串入地线实现取能。二者均存在工程量较大的缺点，其中后者还受应用场合的限制(只宜用于地线接续处以便串入CT)；文献[1]针对典型架空线路地线等效电路参数进行了研究，这种方式也可以取得较大的功率，但由于需要将Zl串入(optical power ground wire，OPGW)，应用范围有限。文献[2]针对典型架空输电线路提出了利用分段绝缘地线取能的方式。该方式可以保证在某一点获得较大的取能功率，但没有就同一条线路上多点取能时的功率分布等进行进一步研究。

为此，文中针对某典型架空输电线路，就一条线路上分布若干个取能点时各取能点的功率进行了理论分析与计算，得到了取能负载的功率分布特性。

1 地线多点取能理论分析

典型的架空输电线路[14-16]一般包含两根地线，一为分段绝缘(即段间绝缘，段内单点接地)的普通地线，一为逐塔接地的光纤复合地线OPGW。由于地线通常是接地的，其静电感应电压为0，因此地线取能主要考虑基于电磁感应的方法。已有研究表明[1-5]，基于电磁感应的取能方法宜通过两架空地线组成闭合回路，由于输电线路周围空间的电磁场在地线回路中产生涡旋感应电动势，将取能负载串入该回路即可实现取能。相应的多点取能原理示意图如图1所示(以三点为例)：

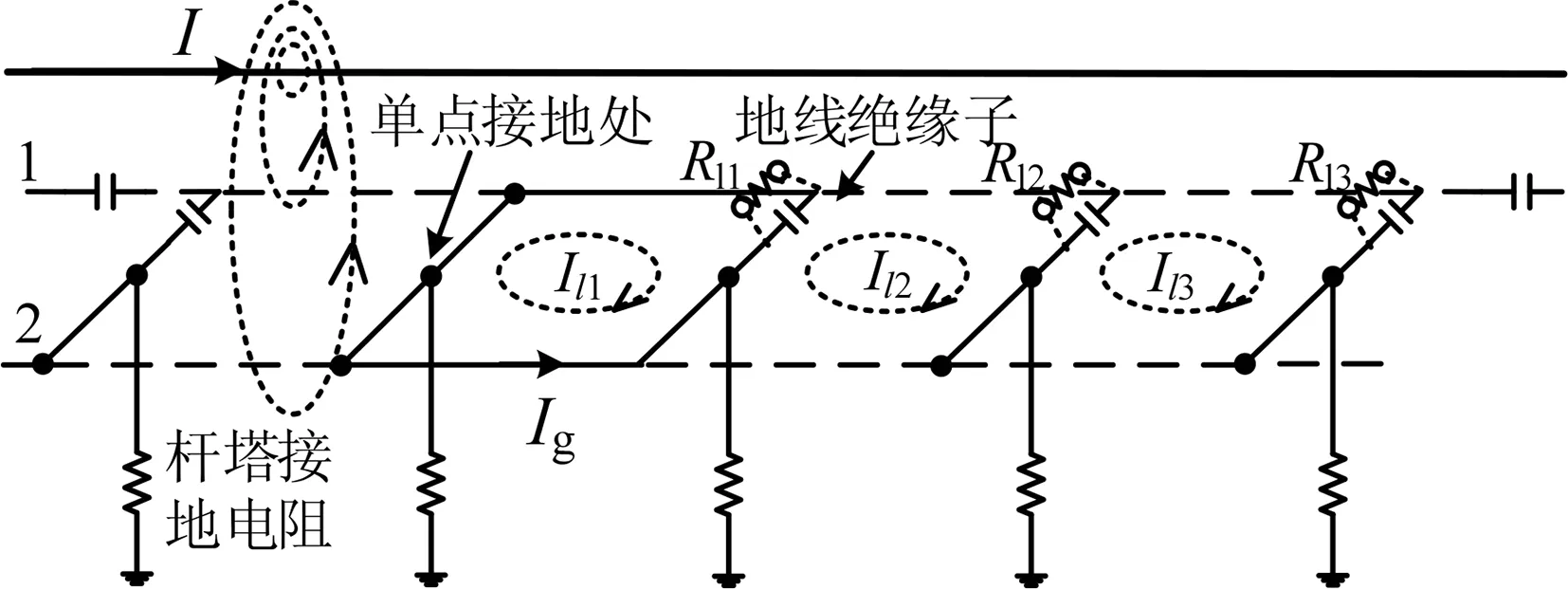
图1 典型架空输电线路地线多点取能示意图Fig.1 Sketch of multi-location power-tapping from ground wire of overhead transmission line

图中1#线为分段绝缘地线，2#线为逐塔接地地线，I表示三相导线的等效电流，l1、l2、l3分别表示架空地线1、2以及取能负载所组成的空间闭合回路，Rl1、Rl2、Rl3分别表示取能负载，Ri，Rj，…，Rn分别表示杆塔接地电阻，Ig表示地线电流(源于涡旋感应)。

由图1可知，导线电流在输电线路周围空间产生工频交变磁场，该磁场在地线回路l1、l2、l3中激发感应电动势，因此在回路中串入负载即可实现取能。

相应的等值计算电路如图2所示：

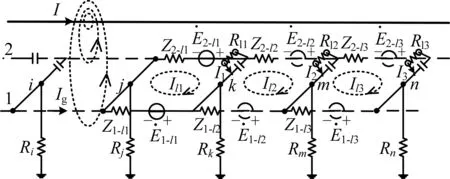
图2 等值计算电路Fig.2 Equivalent calculation circuit

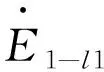
当负载确定时，其功率取决于其电流或电压。由图1或图2可知，负载电流实际上取决于各回路电流(即Il1，Il2，Il3)之差，如I1=Il1-Il2。

以2个负载的情况为例，则由图2可得

(1)

记回路l1、l2的自阻抗分别为Zl1、Zl2，则由式(1)可得负载功率为

(2)

式中P1、P2分别表示负载Rl1、Rl2的取能功率。

当地线自阻抗远远小于负载阻抗(即Zl1≪Rl1，Zl2≪Rl2)时，式(2)可简化为

(3)

方便起见，各相量在后文中用有效值表示。

由式(1)～(3)可知，影响各处取能负载电流(或功率)的因素很多，其解析计算非常复杂，不仅涉及取能负载本身，还包括导线电流，杆塔纵向几何结构，两地线的拓扑结构，杆塔接地电阻及档距分布，地线自感抗等。当负载数量增加时，其计算与分析更加复杂。因此，文章主要通过EMTP-ATP程序对地线多点取能时的负载功率分布特性进行分析计算。

2 仿真分析

2.1 仿真模型介绍

文中以某220kV单回架空输电线路为例进行分析。其纵向几何均值结构如图3所示：

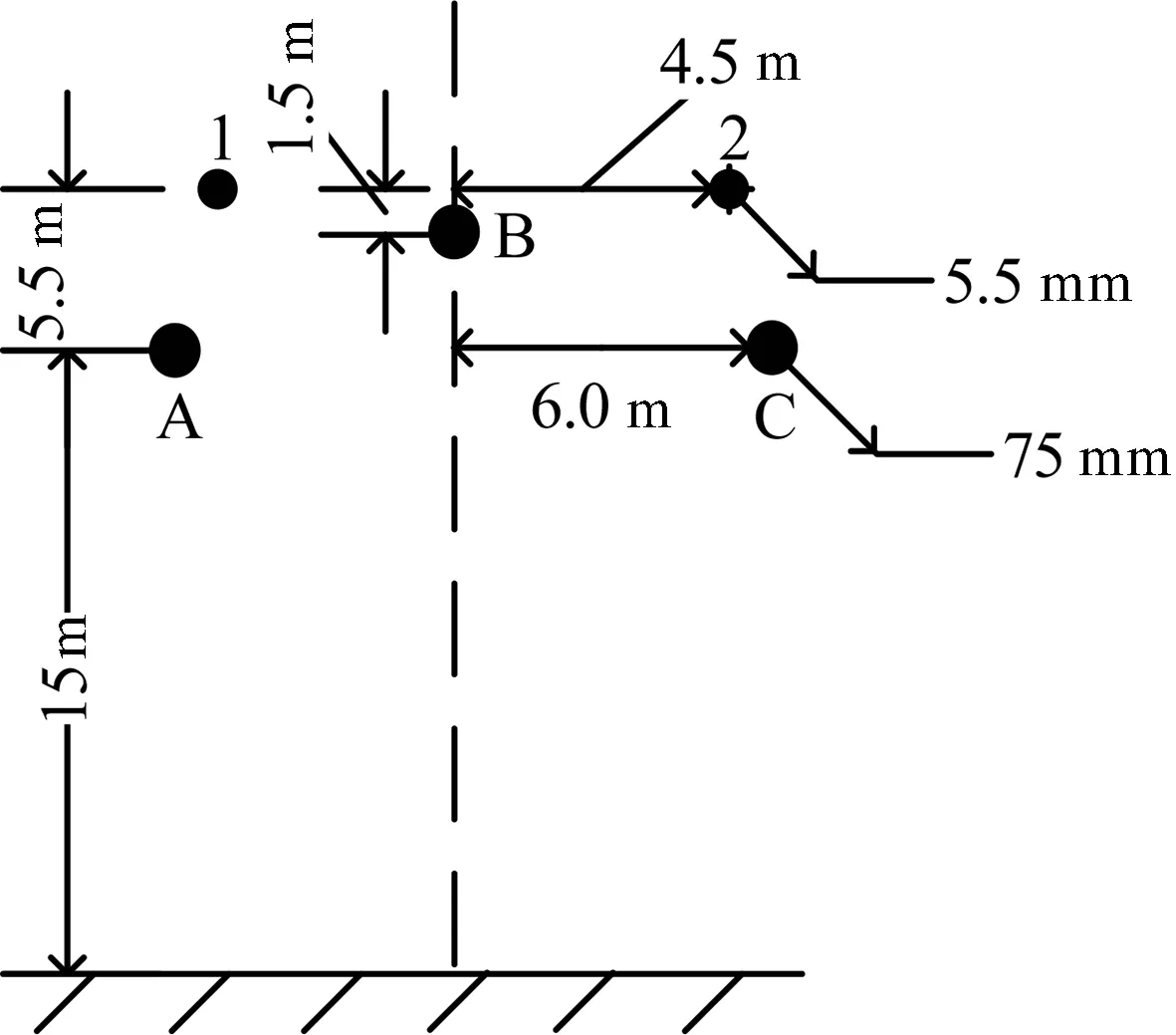
图3 线路纵向几何均值结构示意图Fig.3 Mean longitudinal schematic diagram of the line

图中1为逐基接地地线(计算半径约为7mm，直流电阻约0.8Ω)，2为分段绝缘地线(计算半径约为5.5mm，直流电阻约1.7Ω)，三相导线为2×LGJ-400(直流电阻为0.08Ω，等效计算半径约为75mm)。土壤电阻率约为300Ω·m，杆塔平均接地电阻为10Ω左右，档距均值约为300m。导线计算电流约为400A。

仿真基本方案如下：

1)方便起见，首先取线路参数为均匀参数，取能位置取线路中间区域。在此条件下分析多点取能功率的分布情况；

2)一个取能点的所有负载等效为一个取能负载。多点取能的功率分布主要考察取能负载的变化、负载个数及其相对位置的变化情况。仿真按照取能点(或负载)个数(文中考察2个，3个，4个三种情况)分别进行；

3)首先考察各取能点负载相等时的情况，然后考察负载取值不等时的情况。

线路仿真截图如下：

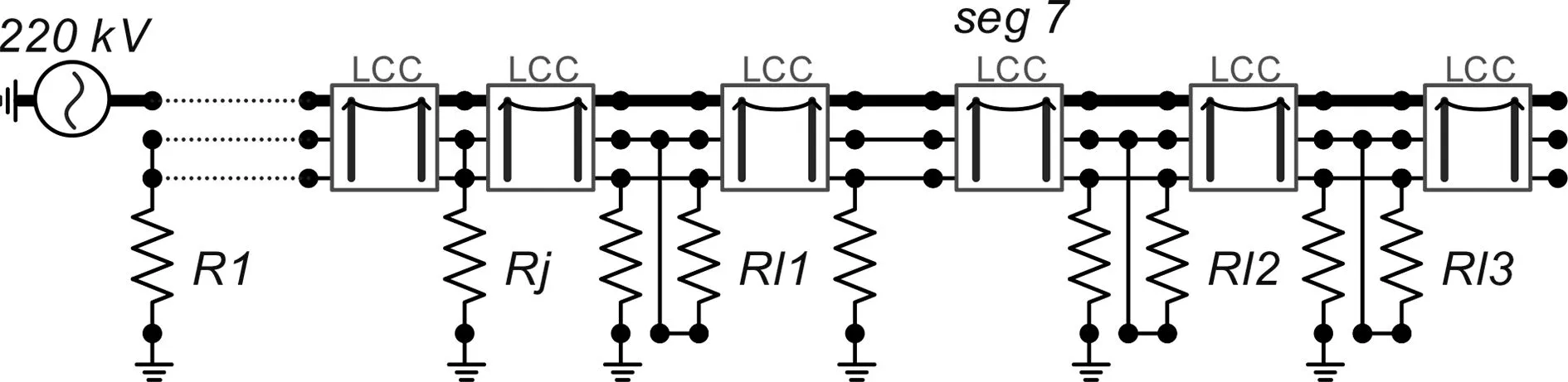
图4 线路仿真示例截图Fig.4 Screen shot of the line simulation example

图中LCC模块表示一档输电线路，Rl1～Rl3、R1、Rj意义同前。

2.2 有关仿真结果

仿真表明，单点接地处两侧的取能负载互不影响。因此，文中着重对位于单点接地处同一侧的取能负载的功率分布特性进行研究。方便起见，负载取能功率的计算结果以其电流表示。

2处取能负载(Rl1=Rl2)时的取能功率计算结果如表1所示：

表1 取能点为2个时的负载电流
Table1Loadcurrentwith2power-tappinglocations

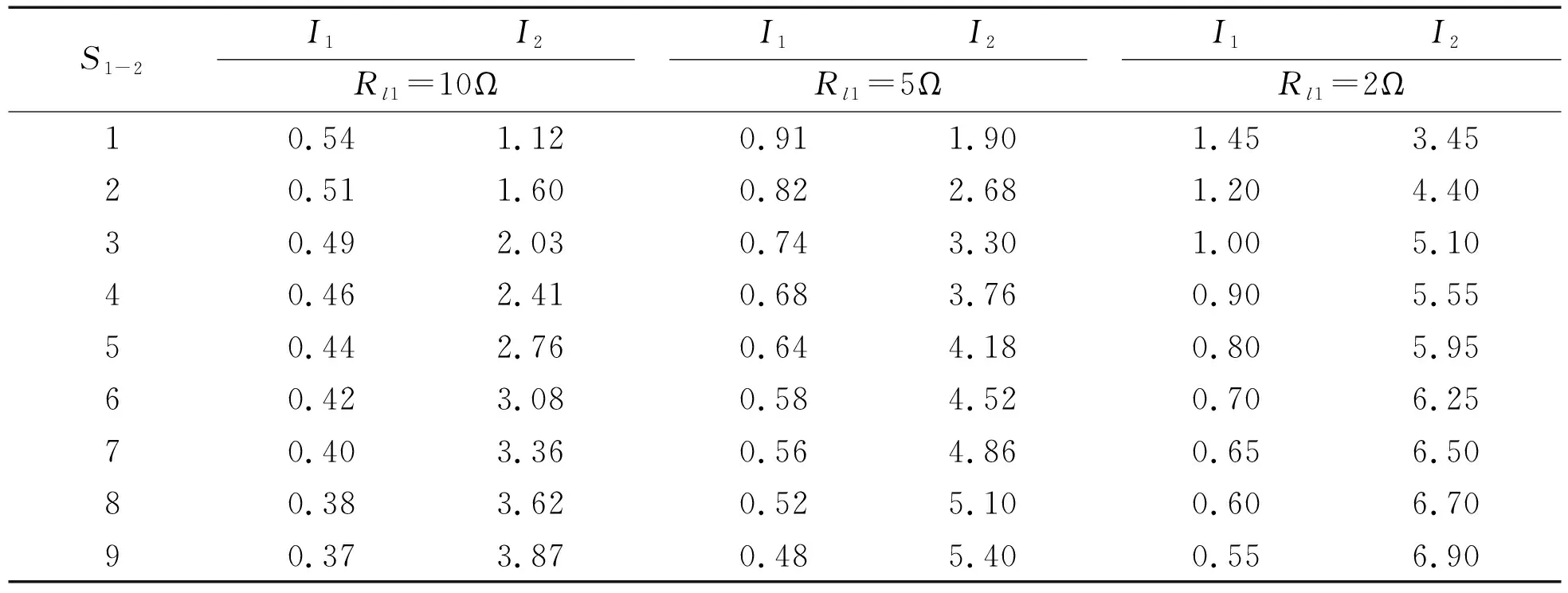
S1-2I1I2Rl1=10ΩI1I2Rl1=5ΩI1I2Rl1=2Ω10.541.120.911.901.453.4520.511.600.822.681.204.4030.492.030.743.301.005.1040.462.410.683.760.905.5550.442.760.644.180.805.9560.423.080.584.520.706.2570.403.360.564.860.656.5080.383.620.525.100.606.7090.373.870.485.400.556.90

表中S1-2表示Rl2距Rl1的档距数(图4中S1-2=2)，S1-2=0时表示只有一个取能负载即Rl1。

以Rl1=Rl2=Rl3=5Ω为例，3处取能负载时的取能功率计算结果如表2所示：

表2 取能点为3个时的负载电流
Table2Loadcurrentwith3power-tappinglocations

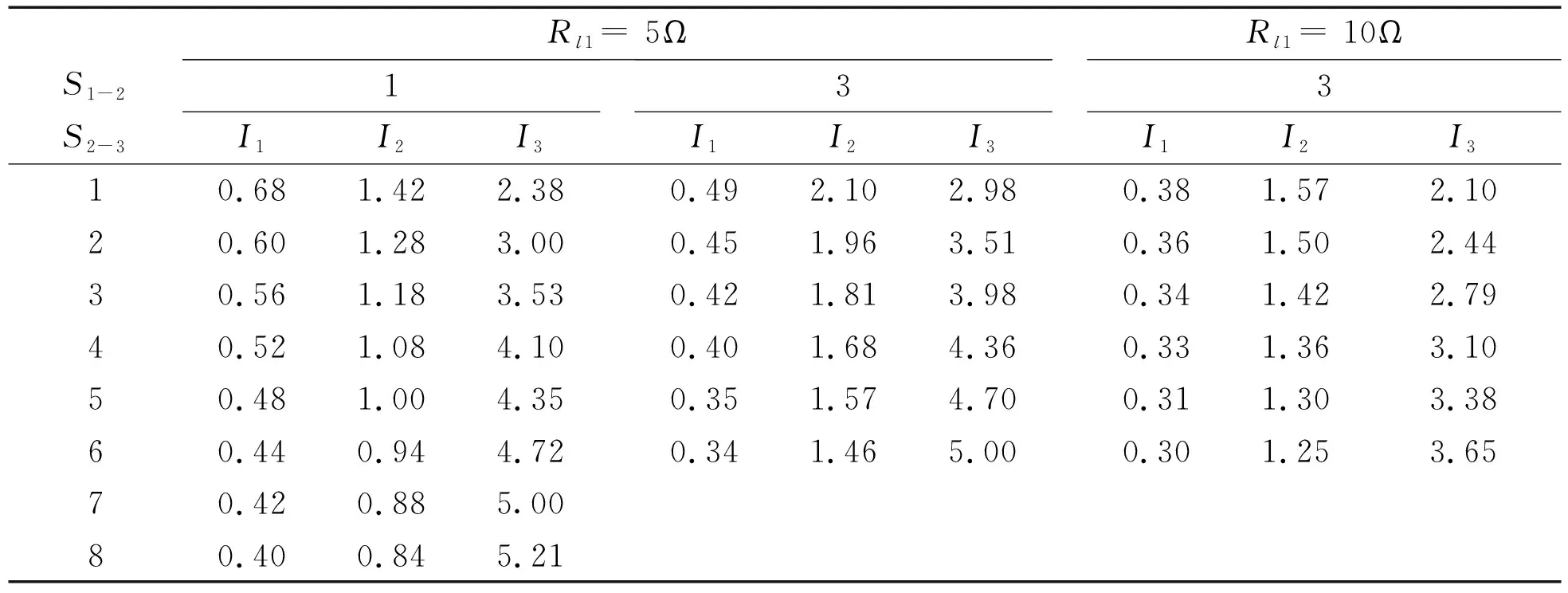
Rl1 = 5ΩRl1 = 10ΩS1-2133S2-3I1I2I3I1I2I3I1I2I310.681.422.380.492.102.980.381.572.1020.601.283.000.451.963.510.361.502.4430.561.183.530.421.813.980.341.422.7940.521.084.100.401.684.360.331.363.1050.481.004.350.351.574.700.311.303.3860.440.944.720.341.465.000.301.253.6570.420.885.0080.400.845.21

表中S2-3表示Rl2距Rl3的档距数(图4中S2-3=1)

4处取能负载(Rl1=Rl2=Rl3=Rl4)时的取能功率计算结果如表3所示：

表3 取能点为4个时的负载电流
Table3Loadcurrentwith4power-tappinglocations

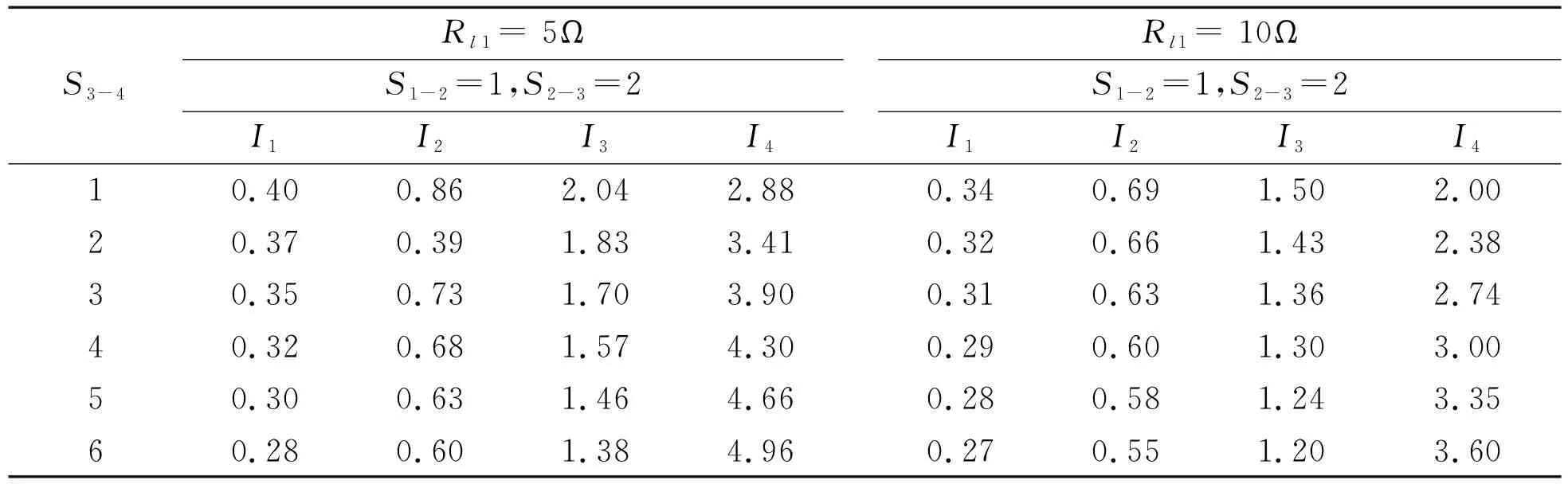
S3-4Rl1 = 5ΩS1-2=1,S2-3=2I1I2I3I4Rl1 = 10ΩS1-2=1,S2-3=2I1I2I3I410.400.862.042.880.340.691.502.0020.370.391.833.410.320.661.432.3830.350.731.703.900.310.631.362.7440.320.681.574.300.290.601.303.0050.300.631.464.660.280.581.243.3560.280.601.384.960.270.551.203.60

表中S3-4表示Rl4距Rl3的档距数。

取能负载不等时(以2处取能负载为例)的功率分布计算结果如表4所示：

表4 负载变化时的负载电流
Table4Loadcurrentwithdifferentpower-tappingloads

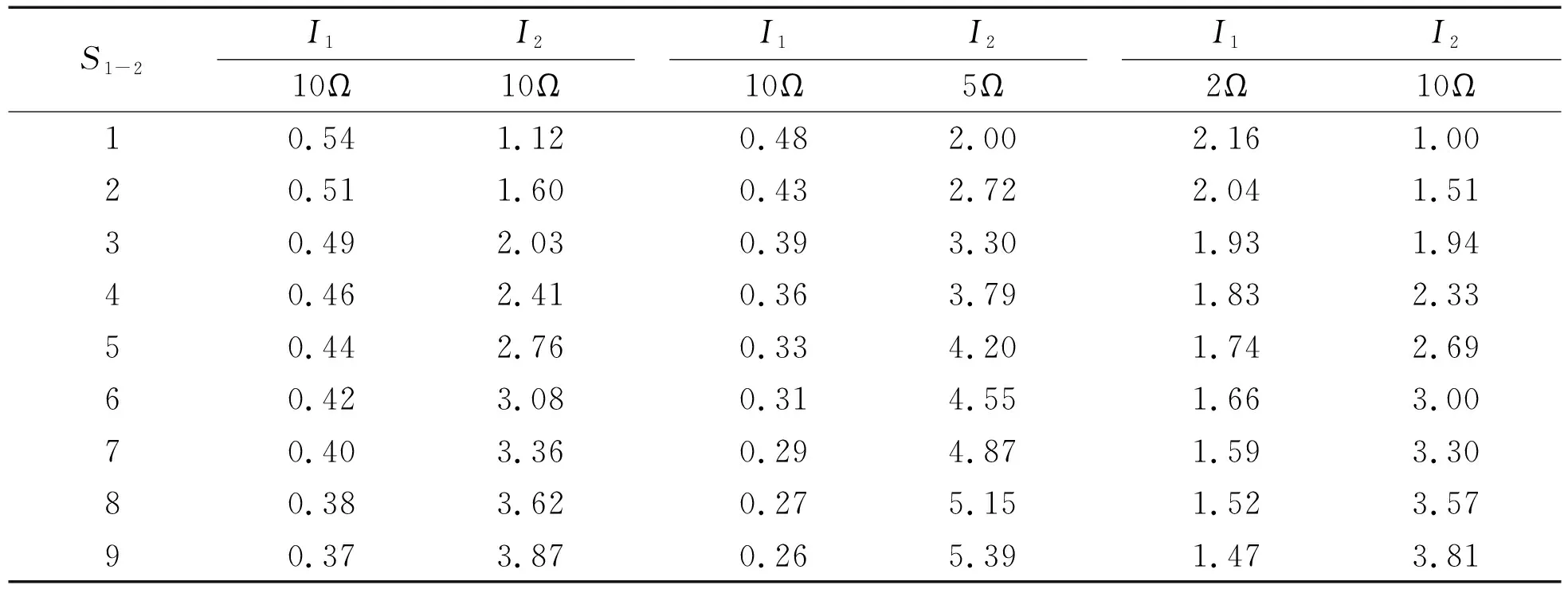
S1-2I1I210Ω10ΩI1I210Ω5ΩI1I22Ω10Ω10.541.120.482.002.161.0020.511.600.432.722.041.5130.492.030.393.301.931.9440.462.410.363.791.832.3350.442.760.334.201.742.6960.423.080.314.551.663.0070.403.360.294.871.593.3080.383.620.275.151.523.5790.373.870.265.391.473.81

2.3 仿真结果的分析

由表1～4分析可知：

对于2处或以上取能负载的情况：

1)由于Il1在Rl1上产生的压降的相位与Il2相反，而回路l2总的感应电动势是不变的，因此Il1会导致Rl2的电流I2增大。I2或Il2(≈(El1+El2)/Rl2)与El2正相关，后者又与S1-2(即取能档距数)成正比，因此I2随着S1-2的增大而增大，同时受Il1或El1的影响逐渐减小。

因此，I2的变化趋势是：随着S1-2的增加而增加，但增幅逐渐降低并趋于稳定；

2)Il2增加时，I1(=Il1-Il2)必将减小，但随着Il2增幅的减小并趋于稳定，I1的降幅也将逐渐减小并趋于稳定。

因此，I1的变化趋势是：随着S1-2的增加而减小，但降幅逐渐降低并趋于稳定；

3)Il1、Il2的相互影响需要通过Rl1传递实现，当Rl1相对回路l1、l2的自阻抗(即Zl1、Zl2)减小时，Rl1的电流(即I1)的变化幅度必然增大；同时，Rl1减小时其对Rl2所在回路的影响也减小，因此I2的变化幅度也减小。

简而言之，Rl1减小，S1-2增加时I1的降幅增大，I2的升幅则减小。

对于3处或以上取能负载的情况：

将负载Rl1、Rl2、Rl3、…(最后一个负载除外)等效为一个取能负载后，可以看做2个负载的情况，则前面所有负载的电流(或功率)的变化特性必然与2个负载的情况中的I1类似，而最后一个负载与I2类似。

此外，无论取能负载为几处，由于取能负载距单点接地处较远时，其取能回路的范围较大，从而使得回路的感应电动势较大。

因此，无论取能点为几处，距离单点接地处较远的取能负载的电流(或功率)均大于较近处的电流(或功率)。例如，对于3处取能负载的情况，有：I3>I2>I1。

3 结论

1)文中针对典型架空输电线路，结合理论计算与EMTP-ATP程序的仿真对地线多点取能时各取能点的功率进行了分析计算，得到了取能负载的功率分布特性。

2)研究表明：最后一个取能负载(即距离单点接地处最远的负载)的功率随前面负载的距离的增加而增加，但增幅逐渐降低并趋于稳定，而前面的负载则随该距离的增加而减小，但降幅幅逐渐降低并趋于稳定。同时，随着取能负载阻抗的减小，最后一个负载电流的变化幅度增大，而前面负载的变化幅度则减小。此外，负载相同时距离单点接地处较远的取能负载的功率大于较近处的取能功率。但是，取能负载位于单点接地处两侧时互不影响；

3)无论各取能负载是否相等，各取能负载的功率分布仍保持同样的变化规律。