带有分数阶边界条件的一维分数阶扩散方程差分方法

刘桃花,侯木舟

(1.湖南科技大学 数学与计算科学学院，湖南 湘潭，411201； 2.中南大学 数学与统计学院，湖南 长沙，410083 )

经典的扩散方程已经普遍地应用于描述粒子的Brown运动,其中,一维扩散方程可以写成下列形式：

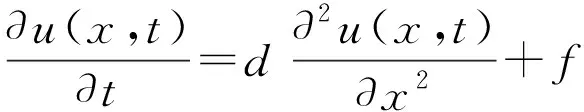
d为扩散系数,f(x,t)为原项。

近十几年来,分数阶在各类学科中的广泛应用,由于多数情况下分数阶偏微分方程的精确解得不到,分数阶偏微分方程数值方法成为求解分数阶偏微分方程的主流方法[6-8]。关于数值方法,Meerschaert和Tadjeran等人[9-11]用有限差分方法求解了单、双边空间的分数阶对流-扩散方程以及用交替方向的隐式差分方法求解了二维空间的分数阶扩散方程；王宏等人[12-13]发展了一系列关于求解空间分数阶微分方程的快速算法,大大降低了计算量和储存量。目前,文献[14]采用了Grünwald改进型的离散方法对带Neumann分数阶边界条件的分数阶微分方程进行离散,构造出分数阶微分方程的显式有限差分格式,并证明了显式格式条件稳定和条件收敛;文献[15]对带分数阶Dirichelet边界条件初边值问题的一维分数阶渗流方程建立了一种隐式有限差分格式,证明了格式的稳定性和收敛性,验证了数值格式的有效性。

考虑如下带分数阶边界条件初边值问题的分数阶对流方程：

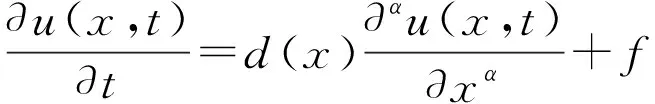
(1)

分数阶初边值条件为

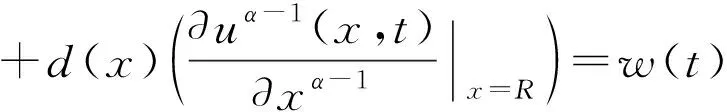
(2)

u(x,0)=q(x)，0≤x≤R

(3)

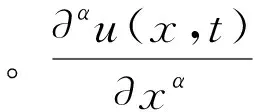
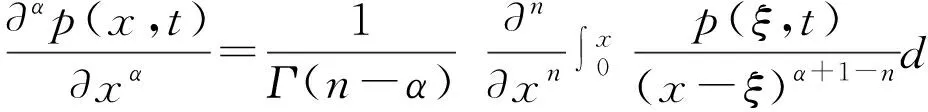
(4)

其中Γ(·)为Gamma函数。

1 差分格式的建立及其相容性

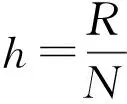
移位的Grünwald-Letnikov分数阶算子定义为

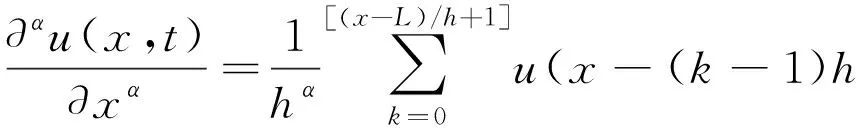
(5)

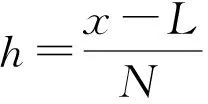
Grünwald权系数定义为

(6)

它的值只依赖于k和α。

标准的Grünwald-Letnikov分数阶算子定义为

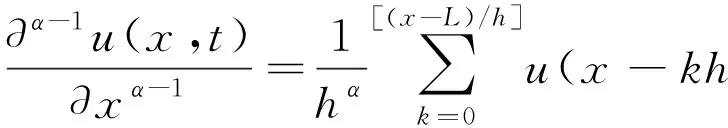
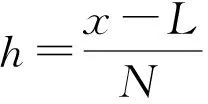
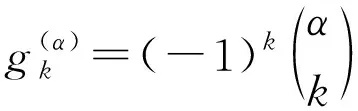
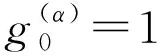
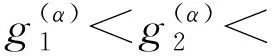
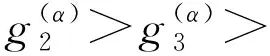
采用移位的Grünwald-Letnikov分数阶算子和标准的Grünwald-Letnikov分数阶算子对方程中Riemann-Liouville分数阶导数以及分数阶边界条件中Riemann-Liouville分数阶导数分别进行离散,得到：

(7)

(8)

利用向后Euler差分方法离散一阶时间导数和一阶空间导数,分别得到：

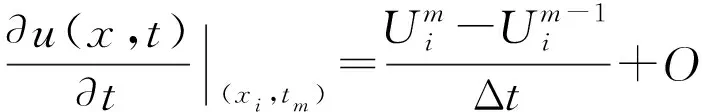
(9)

(10)

对问题(1)-(3)建立差分格式如下：

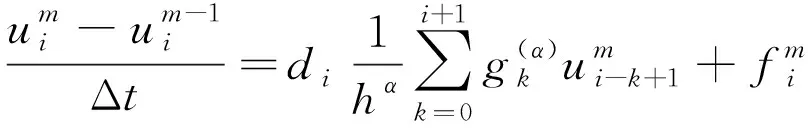
(11)

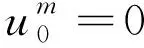
(12)

(13)

当1≤i≤N-1时,局部截断误差为

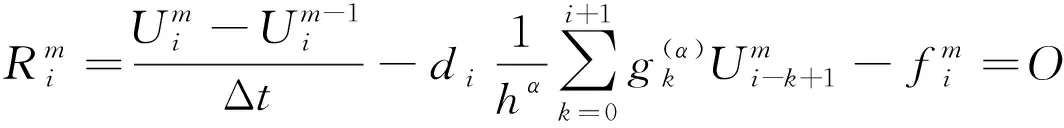
(14)

当i=N时,局部截断误差为

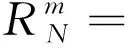
(15)

因此,综上可知,建立的隐式差分格式是相容的。

2 差分格式的差分解的存在唯一性及稳定性和收敛性分析

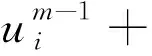
(16)

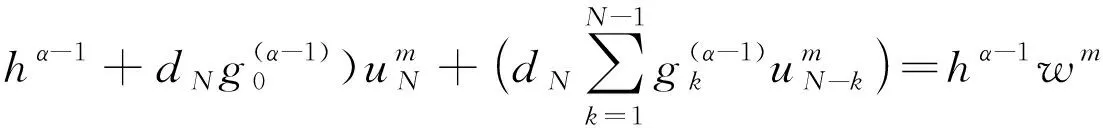
(17)

进一步可以将分数阶方程改写成下列矩阵的形式：

AUm=Qm-1+Fm,1≤m≤M

(18)

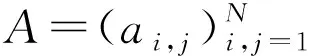
(19)

定理3.1 如果β>0,差分格式(11)-(13)的解存在且唯一。

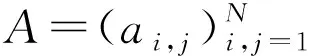
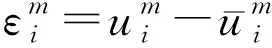
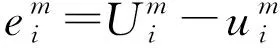
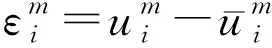
(20)

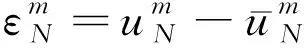
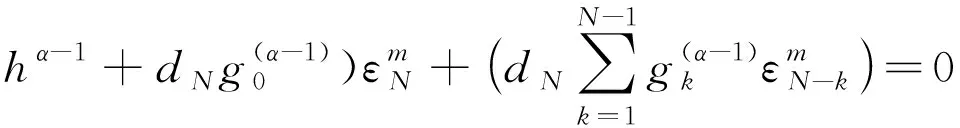
(21)

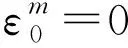
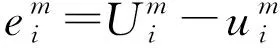
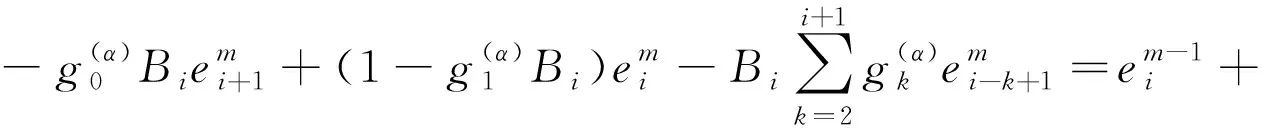
(22)

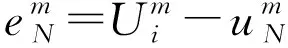
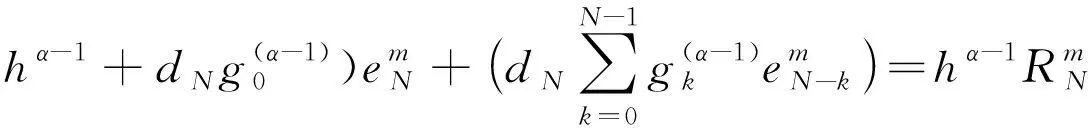
(23)

定理3.2 如果β>0,差分格式(11)-(13)无条件稳定。

证明：由引理2.1得

(24)

由(21)可得

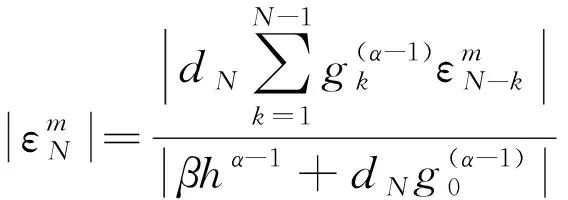
(25)

可以假设‖εm‖≤i0≤N-1),由引理2.1,则有

‖εm‖≤

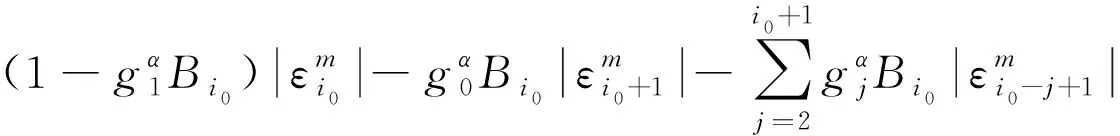
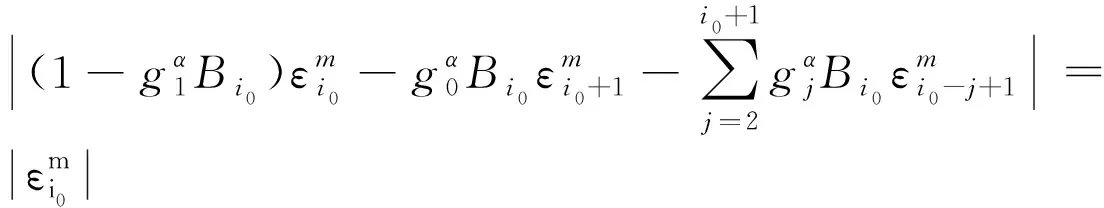
(26)

应用(26)m-1次

‖εm‖<‖ε0‖,1≤m≤M。

综上,差分格式(11)-(13)是无条件稳定的。

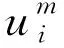
‖em‖≤C(Δt+h),1≤m≤M

(27)

证明：假设‖em‖≥,i=N,由(22)及引理2.1得

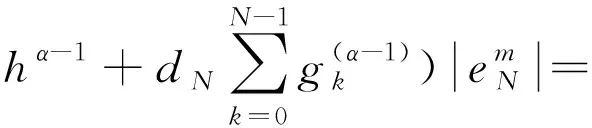
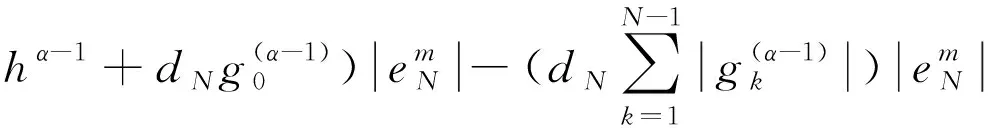
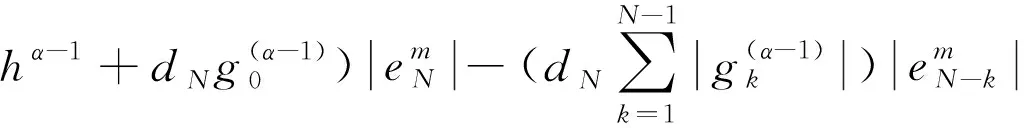
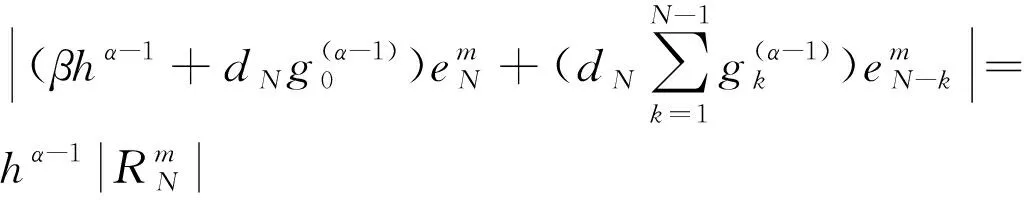
(28)

有引理3.1和Stirling定理(见文献[16]),则有

(29)

当N→,结合(28)和(29),得

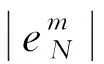
(30)

假设‖em‖≥≤i0≤N-1),则有

‖em‖≤

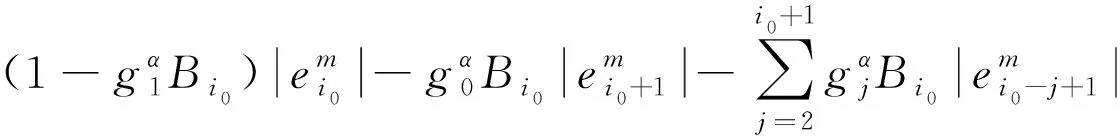
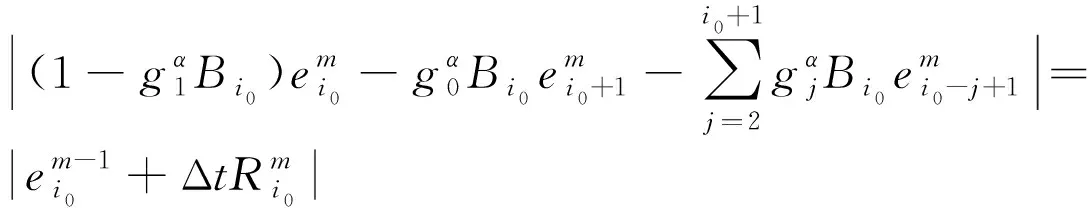
(31)

运用(31)m-1次,则有

‖em‖≤(m-1)ΔtC2(Δt+h)；又因为(m-1)Δt≤T,所以存在一个常数C3=C2T,使得

‖em‖≤C3(Δt+h)

(32)

综上,‖em‖≤C(Δt+h)。

所以此格式收敛。

3 数值试验

取扩散系数d(x)=Γ(2-α)xα-1；原项

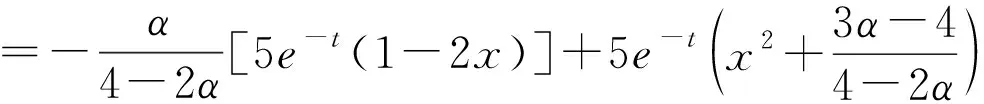
分数阶初边值条件为

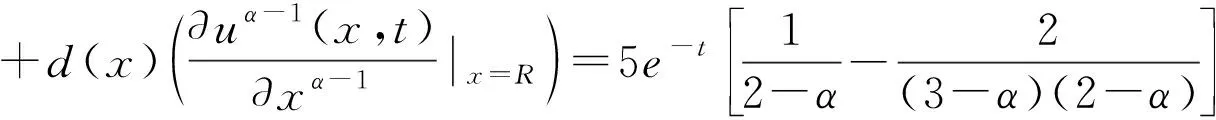
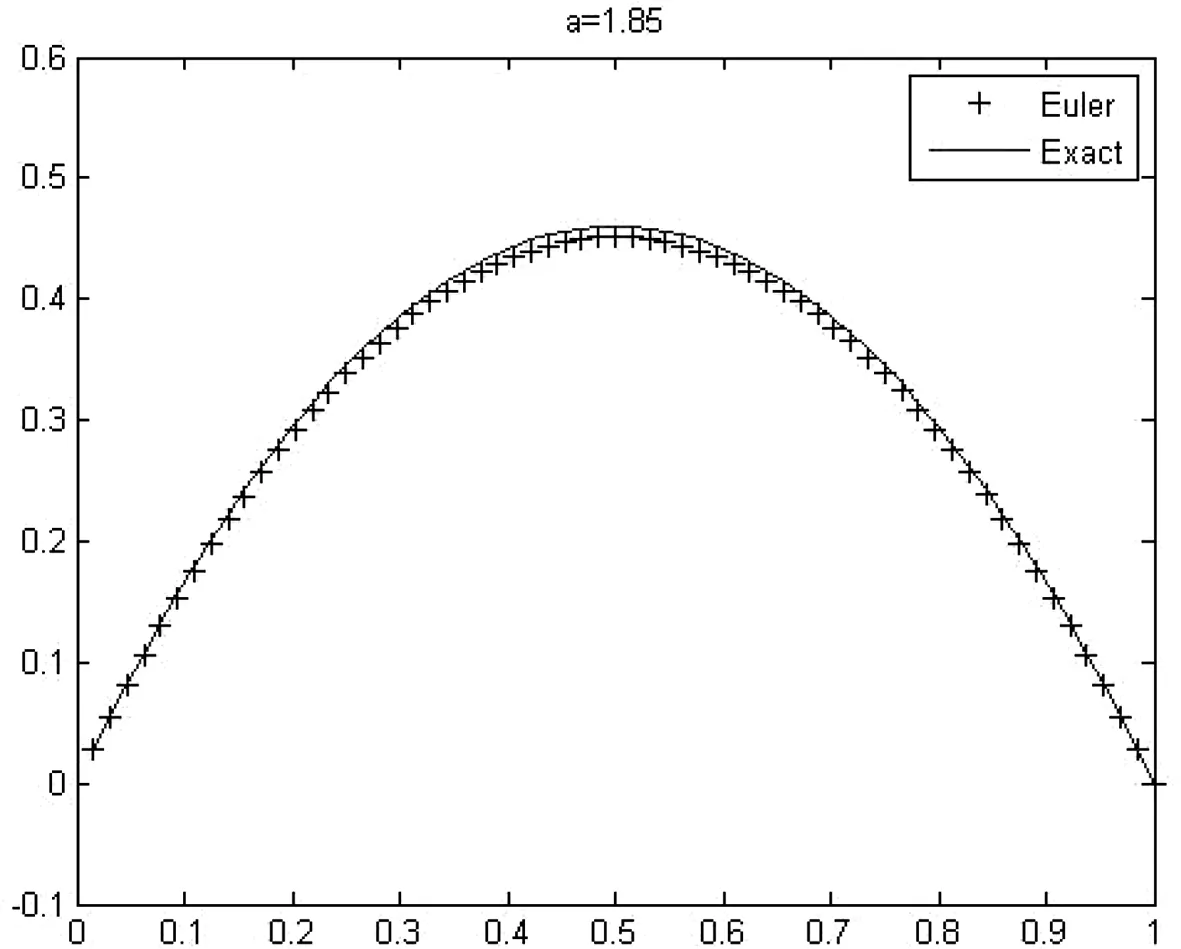
图1 数值结果Fig.1 Numberical results

图1为Δt=h=2-6的网格上,T=1时刻,格式(11)-(13)所得到的数值解以及精确解的图像；从图像可以看到,在本例中数值解可以很好的拟合精确解。

表1表示当T=1时，α分别取1.95,1.85,1.65时算例的数值解与解析离散解之差的最大误差及误差阶。在表1中，当空间步长、时间步长减半时，格式误差接近原来的1/2，这就验证了这个格式的收敛阶为O(Δt+h)。

表1 当T=1时隐式差分格式的误差值
Table1Errorbehaviorsforimplicitfinitedifferencescheme(16)attimeT=1

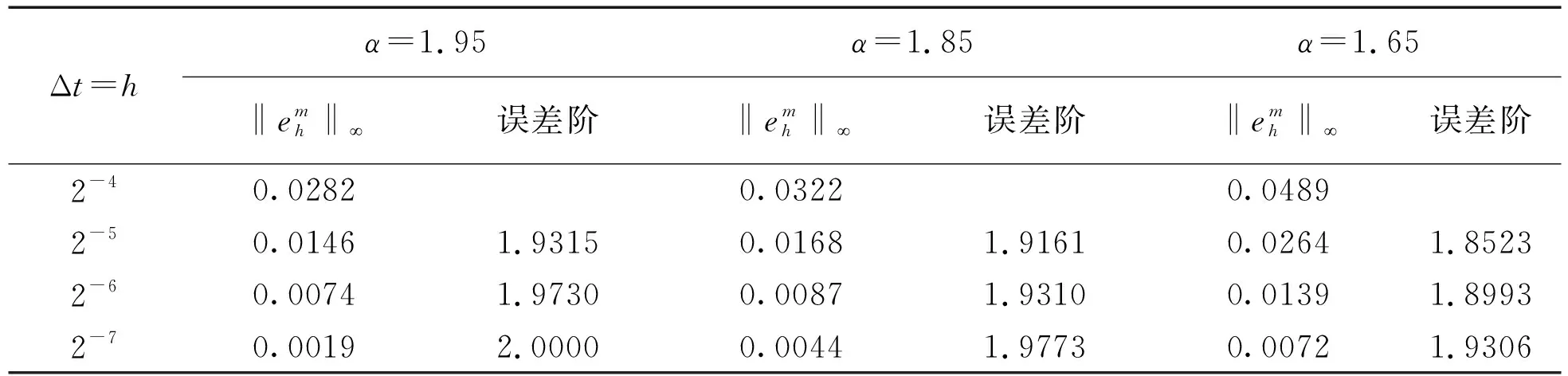
Δt=hα=1.95α=1.85α=1.65‖emh‖呂误差阶‖emh‖呂误差阶‖emh‖呂误差阶2-40.02820.03220.04892-50.01461.93150.01681.91610.02641.85232-60.00741.97300.00871.93100.01391.89932-70.00192.00000.00441.97730.00721.9306

4 结论

考虑了在有界区域里带分数阶边界条件的一维空间分数阶扩散方程,建立了经典的隐性差分格式,证明该格式的解的存在唯一性，无条件稳定性,也证明了这个隐式差分方法收敛于空间分数阶扩散方程的解,且具有O(Δt+h)收敛阶。