双圈图的扩展能量的上界

周后卿

(邵阳学院 理学院，湖南 邵阳，422000)

设G是一个简单图，顶点集为V(G)={v1,v2,…,vn}。用di表示顶点vi的度，同时,分别用Δ、δ表示G中的最大度和最小度。G的邻接矩阵用A(G) 表示,设A(G)的特征值为λi(i=1,2,…,n)。 因为A(G)是一个实对称矩阵，它的所有特征值都是实数，不妨设λ1≥λ2≥…≥λn，G的谱是邻接矩阵A(G)的所有特征值的集合。若G是一个具有顶点n的简单连通图，其边数为n+1，则称G为双圈图。

这篇文章将研究双圈图的扩展能量的上界问题。

1 几个引理

为了证明这篇文章的定理，需要下列几个引理。

引理1[13]设G是一个具有n个顶点的简单图，则

引理2[15]设G是一个具有n个顶点m条边，度序列为d1,d2,…,dn的简单图,则

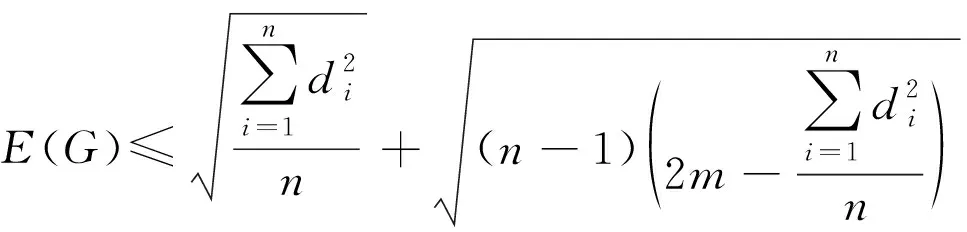
引理3[16]设G是一个具有n个顶点m条边的简单图，

1)若2m≥n，则

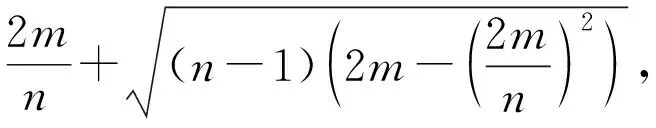
2)若2m≤n，则E(G)≤2m，等式成立当且仅当G是边不相交的并或为孤立顶点。

引理4[17]设G是一个具有n个顶点的简单图，则

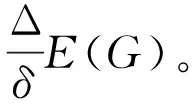
2 主要结论

现在，利用最大度、最小度来证明下面的结论。

定理1 设G是一个具有n个顶点的双圈图，则

因此，对于双圈图来说，若δ=1，则由引理1有

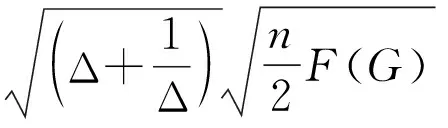
以如下的图1 为例，计算它的扩展能量。

图1 具有7个顶点的双圈图G Fig.1 Bicyclic graph Gwith 7 vertices

利用mathematica软件直接计算双圈图的特征值谱为{2.8558,1,0.3216,0,-1,-1,-2.1774}，得到双圈图的扩展矩阵的特征值谱是{5.6999,1,0.6263,0,-1,-1,-5.3262}，因此可算出扩展能量为Eex(G)=14.6524。 若利用定理1求，由于图G的最大度为6，最小度为1，因此有

定理2 设G是一个具有n个顶点的双圈图，则

又因为G是双圈图，所以m=n+1。

再以图1中的双圈图为例，利用定理2计算，得到Eex(G)≤99，定理是成立的。

证明 因为G是双圈图，于是有m=n+1，根据引理3，

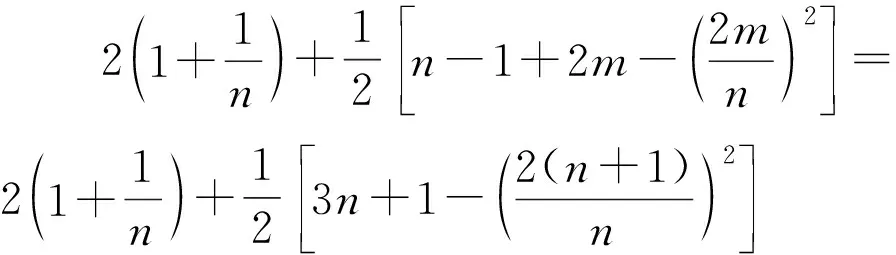
仍以图1中的双圈图为例，利用定理3计算，得到Eex(G)≤64.2857，定理成立。从上面的例子可看出，定理3的结果似乎比另外2个要精确一些。