基于三支决策模型的代价敏感数据分类方法
孙海霞,许厚棣
(1.安徽三联学院,计算机工程学院,安徽 合肥,230601; 2.驻中国电科三十八所军事代表室,安徽 合肥,230088)
三支决策模型[1]是加拿大著名学者Yao在2009年提出的一种决策理论,该模型是在传统的二支决策理论[2]基础上的进一步推广。三支决策模型将决策的结果分为三种形式,分别为接受决策、拒绝决策和延迟决策,对于目前已有的信息不能判断决策对象是否接受或拒绝,三支决策便将这种情况判定为延迟决策,即等待进一步分析[1-2]。由于这种决策模式的新颖性,三支决策理论的提出便立即成为决策分析领域的一个研究热点。
经过这几年的不断研究,三支决策模型目前已经得到了大量的推广和应用。Sun等[3]学者在复杂数据环境下提出了一种组决策模型的三支决策方法;Xu等[4]学者将三支决策运用于流计算方面,提出了一种基于三支决策的流计算学习;在聚类方面,Yu等[5]学者根据三支决策给出一种确定聚类数量的方法,并且进一步提出了数据的三支决策聚类[6];Zhang等[7]学者根据三支决策模型提出了三支个性化推荐算法;在其他应用领域,Nauman等[8]学者将三支决策模型运用于软件的测试和分析;谢骋等[9]学者运用三支决策提出一种视频异常行为检测方法;Zhou等[10]学者运用三支决策用于邮箱垃圾邮件的检测;李建林等[11]学者将三支决策运用于垃圾短信的判别和分析;张越兵等[12]学者将三支决策运用于自然语言处理中,提出一种文本的情感分类方法。总之,目前的三支决策模型已经应用于各个信息领域之中。
三支决策作为一种优越的决策模型,然而目前很少运用于数据的分类中,因此在文中根据三支决策提出一种代价敏感的数据分类方法,首先根据三支决策模型,提出一种新的误分类代价定义,并且提出启发式搜索的最小化误分类代价特征选择算法,根据该特征选择算法得到的特征子集,进一步提出三支决策模型的代价敏感数据分类算法,该算法将分类结果分成三个部分,即标记为特定类、不标记为特定类以及暂不标记,使得分类的结果更加具体明确。最后通过仿真实验,验证了文中所提出的算法具有更高的分类性能。
1 三支决策模型
在分类学习等任务中,数据集一般表示成S=(U,At),其中U为整个数据集S的样本集,∀x∈U称为样本集U中的样本,At为整个数据集的特征集。对于一个标记类别的数据集表示为S=(U,At=C∪d),这里的U同样为整个数据集S的样本集,C称为特征集At中的条件特征集,d为类特征,那么U中的样本x可以表示为〈x,y〉,其中y为样本x的类标记。
对于二分类问题,设分类的结果包含两个类别Ω={Cl,~Cl},三支决策将分类的结果表示成动作集A={aP,aB,aN},其中aP、aB和aN分别表示样本被分类为类别Cl的正区域POS(Cl)、边界域BUN(Cl)和负区域NEG(Cl)。当样本原本属于类别Cl,而被分类进Cl的正区域、边界域和负区域所产生的代价分别为λPP、λBP和λNP;当样本原本不属于类别Cl,而被分类进Cl的正区域、边界域和负区域所产生的代价分别为λPN、λBN和λNN,这些类别代价可以构成一个代价矩阵,具体如表1所示[1]。
表1 分类代价矩阵
Table1Classifiedcostmatrix

原本类别POS(Cl)BUN(Cl)NEG(Cl)ClλPPλBPλNP~ClλPNλBNλNN
根据表1中各类情形的分类代价矩阵,可以得到进行三种决策时的决策代价。对于样本x,类别集Ω={Cl,~Cl},样本x进行aP、aB和aN三种决策动作的预期代价分别为
c(aP|x)=λPP·P(Cl|x)+λPN·P(~Cl|x);
c(aB|x)=λBP·P(Cl|x)+λBN·P(~Cl|x);
c(aN|x)=λNP·P(Cl|x)+λNN·P(~Cl|x)。
这里的P(Cl|x)表示样本x关于类别Cl的条件概率,即样本对类别Cl的隶属程度。c(aP|x)、c(aB|x)和c(aN|x)即为样本分类入类别Cl的正区域、边界域和负区域时所产生的分类代价。
Yao认为在三种决策动作中,分类代价最小的决策行为即为最佳的决策,因此Yao根据这一思想提出了三支决策规则[1-2],即:
1)如果c(aP|x) 2)如果c(aB|x) 3)如果c(aN|x) 三支决策模型表明,如果样本x分类入类别Cl正区域的代价是最小的,那么就直接将样本x分类入类别Cl。如果样本x分类入类别Cl负区域的代价是最小的,那么就直接将样本x分类入类别~Cl。如果样本x分类入类别Cl边界域的代价是最小的,那么三支决策模型认为样本x的分类情况不确定,因此对于样本x进行延迟决策并作进一步分析[1-2],正是由于这种延迟决策,使得三支决策模型在决策应用中具有更好的优越性[2]。 根据三支决策模型的决策模式,文章将提出一种三支决策的数据分类方法。 在数据分类任务中,数据集中大量的特征不仅影响了分类算法的学习效率,而且数据集中的很多特征包含了冗余和不相关的信息,这些特征的存在不利于分类算法的分类性能[13]。为了改善这类问题,常用的处理方法便是特征降维,即特征选择[14]。在文章中首先提出一种最小化误分类代价的特征选择算法,然后进一步的提出三支决策的代价敏感数据分类。 对于二分类问题,设类标记数据集为S=(U,C∪d),给定样本x和特征子集B⊆C,类别划分为Ω={Cl,~Cl},类别Cl的代价矩阵如表1所示,令给定样本x在特征子集B下的三支决策结果为ΓB(x)。基于这个结果提出三支决策模型下样本x的误分类代价mcB(x),其定义为 1)当ΓB(x)=POS(Cl),那么mcB(x)=λPN·PB(~Cl|x); 2)当ΓB(x)=BUN(Cl),那么mcB(x)=λBP·PB(Cl|x)+λBN·PB(~Cl|x); 3)当ΓB(x)=NEG(Cl),那么mcB(x)=λNP·PB(Cl|x)。 这里的PB(Cl|x)和PB(~Cl|x)分别表示样本x关于类别Cl和~Cl在特征子集B下的条件概率。根据三支决策模型,若样本x判定为类别Cl,那么误分类代价即为样本x原先属于类别~Cl而判定为类别Cl时所付出的代价,因此代价结果为λPN·PB(~Cl|x)。同理若样本x判定为类别~Cl,那么误分类代价即为样本x原先属于类别Cl而判定为类别~Cl时所付出的代价。若样本x判定结果为进一步分析,那么误分类代价为x原先属于类别Cl或x原先属于类别~Cl时两种情况代价之和。 在误分类代价的计算中,代价矩阵是一个事先给定的常量,因此误分类代价的结果取决于条件概率PB(Cl|x)和PB(~Cl|x)。对于给定的样本x和类别划分Ω={Cl,~Cl},不同特征子集B下,将有不同的PB(Cl|x)和PB(~Cl|x)值,因此可以看出误分类代价的大小与特征子集B直接相关。考虑S=(U,C∪d)的代价敏感分类,目标是对于特征集C寻找出一个特征子集B′,使得样本空间U中所有对象的误分类代价之和最小,具体如定义1所示。 定义1 对于数据样本集S=(U,C∪d),类别划分为Ω={Cl,~Cl},并且类别的代价矩阵如表1所示。若特征子集B′⊆C是样本集S的一个最小误分类代价特征子集,那么必须同时满足: 定义1表明,找到最小误分类代价特征子集B′可以通过遍历特征集C的所有子集来实现,当特征集C规模较小时,可以采用这种方法,但是当特征集C规模较大时,其求解的计算量非常巨大,因而这种方法不再适用。求解特征子集通常采用启发式搜索的方法来逼近理论结果[14],文章在其他学者相关研究的基础上[14-15],提出一种特征重要度的启发式函数,用于特征选择结果的启发式搜索。 sigB(a)=MC(B)-MC(B∪{a})。 根据定义2中关于特征重要度的启发式函数,可以进一步的提出基于启发式的最小误分类代价特征选择算法,具体算法如图1所示。 输入:数据样本集S=(U,C∪d),类别代价矩阵 输出:最小误分类代价特征子集BStep1:初始化B=∅,对特征集C中的每个特征计算误分类代价,选择误代价最小的特征加入B中,即B=B∪argmin∀a∈CMC({a})。Step2:对于∀a∈C-B,计算特征a的重要度sigB(a)=MC(B)-MC(B∪{a})。Step3:找出Step2中sigB(a)值最大的特征,记为a。Step4:判断sigB(a)值的大小,若sigB(a)>0那么B=B∪{a},并重新进入Step2,若sigB(a)≤0,那么进入Step5。Step5:返回特征子集B 图1最小误分类代价特征选择算法 Fig.1The feature selection algorithm of minimum misclassification cost 图1中算法是一个贪心选择的过程,算法在每轮的迭代过程中,通过选取局部最优值来确定特征,直到在候选特征集中没有能使总误分类代价进一步减小的特征时,此时终止算法,输出特征子集结果。 在2.1节中,提出了最小误分类代价特征选择算法,接下来在其基础上提出三支决策模型的代价敏感数据分类方法。 对于样本对象x,类别代价矩阵如表1所示,可以得到: 若c(aP|x) λPP·P(Cl|x)+λPN·P(~Cl|x)≤λBP·P(Cl|x)+λBN·P(~Cl|x) 若c(aB|x) λBP·P(Cl|x)+λBN·P(~Cl|x)≤λPP·P(Cl|x)+λPN·P(~Cl|x) 若c(aN|x) λNP·P(Cl|x)+λNN·P(~Cl|x)≤λPP·P(Cl|x)+λPN·P(~Cl|x) 由于P(Cl|x)=1-P(~Cl|x),所以 1)若P(Cl|x)≥α且P(Cl|x)≥γ,那么x分类入POS(Cl); 2)若P(Cl|x)<α且P(Cl|x)>β,那么x分类入BUN(Cl); 3)若P(Cl|x)≤β且P(Cl|x)≤γ,那么x分类入NEG(Cl)。 这里的 根据上面一系列的推导可以发现,在给定类别代价矩阵的基础上,只需要计算样本x关于类别Cl的条件概率,将这个条件概率与阈值α,β和γ之间进行比较便可以判定x与Cl之间的关系,即样本x是否标记为类别Cl或不作分类进一步分析。因此接下来最关键的问题是研究样本与类别之间条件概率的估计,文中采用文献[16]的处理方法,通过类别占据样本邻域的比重来进行评估概率。 定义3[16]对于数据样本S=(U,C∪d),特征子集B⊆C,并且B中的离散型特征集表示为B1,连续型特征集表示为B2,那么样本x∈U在特征子集B下的邻域样本集定义为 δB(x)={y∈U|dB2(x,y)≤δ∧(∀b∈B1,xb=yb)} 其中xb和yb分别表示样本x和y在特征b下的取值,dB2(x,y)表示样本x和y的距离度量,δ为邻域半径。 解决条件概率的计算问题后,另一个需要解决的问题是,文章之前的假设全部基于二分类问题进行讨论,而现实中的分类问题一般都是多分类的,对于这类情形,可以将多分类问题转化为二分类情形进行分析。对于多分类问题,若样本数据的类别划分为Ω={Cl1,Cl2,…,Clm},需要对每个类别Cli设定分类代价矩阵,如表2所示。 表2 类别Cli代价矩阵 原本类别POS(Cli)BUN(Cli)NEG(Cli)CliλiPPλiBPλiNP~CliλiPNλiBNλiNN 根据多分类情形下各个类别的代价矩阵,便可以给出基于三支决策模型的数据分类方法,具体算法如图2所示。 输入:样本数据集S=(U,C∪d),类别划分Ω={Cl1,Cl2,…,Clm},类别Cli(1≤i≤m)的代价矩阵,算法1选择出的特征子集B,待标记类别的测试样本x;输出:测试样本x的类标记。Step1:初始化类别序号k=0。Step2:根据类别Cli(1≤i≤m)的代价矩阵计算出对应的阈值αi,βi和γi。Step3:k=k+1,并计算测试样本x关于Clk的条件概率P(Clk|x)。Step4:若P(Clk|x)≥αk且P(Clk|x)≥γk,那么进入Step5;若P(Clk|x)<αk且P(Clk|x)>βk,那么进入Step6;若P(Clk|x)≤βk且P(Clk|x)≤γk,那么进入Step3。Step5:将测试样本x标记为类别Clk,算法终止。Step6:对测试样本x暂不进行类别标记并作进一步分析,算法终止。 图2三支决策模型的代价敏感数据分类算法 图2中算法相当于将测试样本x对类别划分Ω={Cl1,Cl2,…,Clm}中每个类别进行三支决策分析。算法刚开始时,首先将x对{Cl1,~Cl1}进行判别,如果P(Cl1|x)≥α1且P(Cl1|x)≥γ1,那么将样本x标记为Cl1;如果P(Cl1|x)<α1且P(Cl1|x)>β1,那么延迟样本x的判别;如果P(Cl1|x)≤β1且P(Cl1|x)≤γ1,那么将测试样本x判别为~Cl1,由于~Cl1=Cl2∪Cl3…∪Clm,因此需要重复如上步骤在{Cl2,~Cl2}中进行分析,然后一直按照这样的流程最后便可以确定x的分类情况。 在本节中将所提出的三支决策模型的代价敏感分类算法与支持向量机分类算法(SVM)、朴素贝叶斯分类算法(NB)以及决策树分类算法(C4.5)对同一组数据集进行分类学习,然后比较他们的分类结果性能,从而验证文中算法的有效性。实验中所运用的6个UCI数据集如表3所示。 表3 实验数据集 编号数据集样本特征类1glass214962wdbc5693023credit6901524car1728645abalone41778296chess28056618 在进行实验之前,首先介绍本实验相关的实验设置问题。文中所提出的分类算法中,样本关于类别的条件概率估计至关重要,文中通过样本的邻域样本集在类别上占据的比重作为条件概率的计算,其中涉及一个参数,即邻域半径δ。在文献[17]中,徐波等学者提出了一种自适应的邻域半径设定方式。 对于连续型特征子集B={b1,b2,…,bc},设特征子集B下的邻域半径集为εB={εb1,εb2,…,εbc},其中 本实验同样采用徐波等[17]学者的方法进行邻域半径的设定,并将调整参数ω的值取为2进行实验。 在算法2中,样本数据中每个类别都需要设定代价矩阵,对于Ω={Cl1,Cl2,…,Clm},Cli的分类代价矩阵设置如表4所示。 表4 类别Cli代价矩阵设置 原本类别POS(Cli)BUN(Cli)NEG(Cli)CliλiPP=0λiBP∈[0,1]λiNP=3λiBP~CliλiPN=3λiBNλiBN∈[0,1]λiNN=0 文中将参与实验的所有分类算法按照十折交叉的方式对表3中的各个数据集进行分类实验。设nPP表示被分类正确的样本数量,nBP表示被延迟分类的样本数量,nNP表示被错误分类的样本数量,那么分类准确率accuracy和分类覆盖率coverage分别表示为 进一步可以得到F-measure为 文中所提出的三支决策模型分类算法为TWD,表5所示的是四种分类算法在各个数据集下的分类准确率,其中结果采用“均值±标准差”的格式来表示。观察表5可以看出,文中所提出的TWD分类算法在大部分数据集中具有更高的分类准确率,这主要是由于TWD在传统分类方法的基础上建立了一种延迟决策的方式,在分类中对于模棱两可的对象给予暂不分类的处理,这样减小了数据误分类的样本数量,提高了分类准确率。而在少部分数据集中,其他分类算法的准确率更高一点,例如SVM分类算法在数据集wdbc上的分类准确率更高,C4.5分类算法在chess上的分类准确率更高。这主要是由于在wdbc数据集中,每个特征均为连续型的,并且只有两个类别,SVM作为一种建立在统计学习基础上的分类模型,对于这类问题具有更好的分类效果。而对于数据集chess,其每个特征均为离散类型的,C4.5算法是一种基于决策树的分类算法,仅适用于离散型数据的分类,同时对离散型数据也具有较好的分类效果,因此C4.5算法在数据集chess上的分类准确率稍高。不过仔细比较一下可以发现,在数据集wdbc和chess中,TWD分类算法的准确率也仅次于最高的分类准确率,因此可以看出TWD分类算法同样具有较高的分类性能。 表5 各个分类算法分类结果的准确率比较 分类算法各数据集分类准确率glasswdbccreditcarabalonechessSVM0.6256±0.01240.9846±0.00630.8257±0.00550.8694±0.01470.9656±0.00390.7636±0.0125NB0.6628±0.00850.9551±0.00730.8157±0.00670.8519±0.01180.9282±0.00760.7573±0.0198C4.50.6852±0.01450.9372±0.01060.7974±0.01000.8369±0.01430.9551±0.00540.7965±0.0187TWD0.7185±0.00760.9673±0.00820.8414±0.00470.8864±0.01220.9762±0.00270.7752±0.0128 表6所示的是四种分类算法在各个数据集下的F-measure值,其结果同样采用“均值±标准差”的格式来表示,观察表6可以看出,TWD分类算法的F-measure值均比其余三种算法要低,这主要是由于在TWD分类算法中,由于有样本延时分类情况的存在,因此分类覆盖率coverage的值小于1,而其余三种算法的分类覆盖率coverage的值等于1,因此TWD分类算法的F-measure值会偏低一点。 表6 各个分类算法分类结果的F-measure比较 分类算法各数据集分类F-measure值glasswdbccreditcarabalonechessSVM0.8337±0.00540.9723±0.00610.8435±0.00640.8747±0.01410.9734±0.01190.8025±0.0112NB0.8416±0.00650.9455±0.00430.8271±0.01170.8994±0.01260.9417±0.00850.7924±0.0152C4.50.8873±0.01050.9638±0.00760.8054±0.00920.8564±0.01210.9535±0.01240.7865±0.0147TWD0.8273±0.00610.9538±0.00420.8244±0.01170.8543±0.01020.9525±0.00770.7652±0.0088 在基于代价敏感的分类算法中,误分类代价是衡量分类性能的又一重要指标。表7所示的是四种算法分类结果的误分类代价,观察表7可以看出,文中所提出的TWD分类算法在所有数据集上具有最小的误分类代价,这主要是由于两个方面,第一是TWD分类算法在进行分类之前,已对样本数据进行了最小化误分类代价的特征选择,然后利用选择后的特征子集进行数据分类,从而使得整体的误分类代价很低,另一方面,TWD分类算法的分类结果中包含延迟决策的分类情形,即对于分类不确定的样本进行了延迟分类,进一步降低了最终分类结果的误分类代价,因此综合起来TWD算法具有更小的误分类代价。 表7 各个分类算法分类结果的误分类代价比较 分类算法各数据集分类误分类代价glasswdbccreditcarabalonechessSVM35.63±13.536.84±3.1716.55±2.55156.46±15.47165.63±9.592836.96±20.25NB25.82±11.867.95±4.2315.78±3.43144.28±10.18189.27±10.763164.25±27.98C4.531.47±11.259.67±5.1213.51±4.25134.46±11.44175.39±12.202465.86±22.47TWD22.56±10.165.63±2.2611.48±3.28121.46±13.62150.63±11.242352.51±28.28 根据以上相关的实验结果,可以证明文中所提出的三支决策模型的分类算法具有更好的代价敏感分类效果。 三支决策是近年来提出的一种新形式的决策理论模型,它通过对决策结果引入一种延迟决策的方式,使得更加适用于现实环境下决策应用。在文中三支决策模型的基础上提出一种代价敏感的数据分类算法。首先根据三支决策模型,提出了数据分类问题中的误分类代价,并基于启发式搜索提出了数据集的最小化误分类代价的特征选择算法,然后根据该特征选择算法得到的特征子集,提出基于三支决策模型的数据分类算法,该算法在数据分类过程中,加入了一种延迟分类的结果形式,使得提高了数据的分类性能,实验分析表明该分类算法具有更高的分类优越性。在将来的研究中,可以致力于更加复杂数据环境下三支决策模型的分类应用。2 三支决策模型的代价敏感数据分类
2.1 最小化误分类代价特征选择

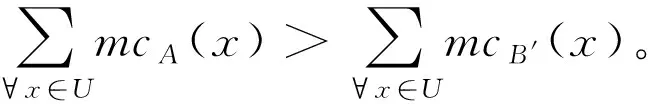
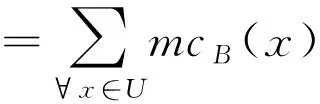

2.2 三支决策模型的代价敏感数据分类
λPP·P(Cl|x)+λPN·P(~Cl|x)≤λNP·P(Cl|x)+λNN·P(~Cl|x)
λBP·P(Cl|x)+λBN·P(~Cl|x)≤λNP·P(Cl|x)+λNN·P(~Cl|x)
λNP·P(Cl|x)+λNN·P(~Cl|x)≤λBP·P(Cl|x)+λBN·P(~Cl|x)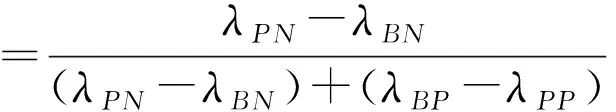
Table2ThecostmatrixofclassCli
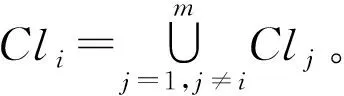

Fig.2The cost-sensitive data classification algorithm of three-way decision models3 实验分析
Table3Experimentaldataset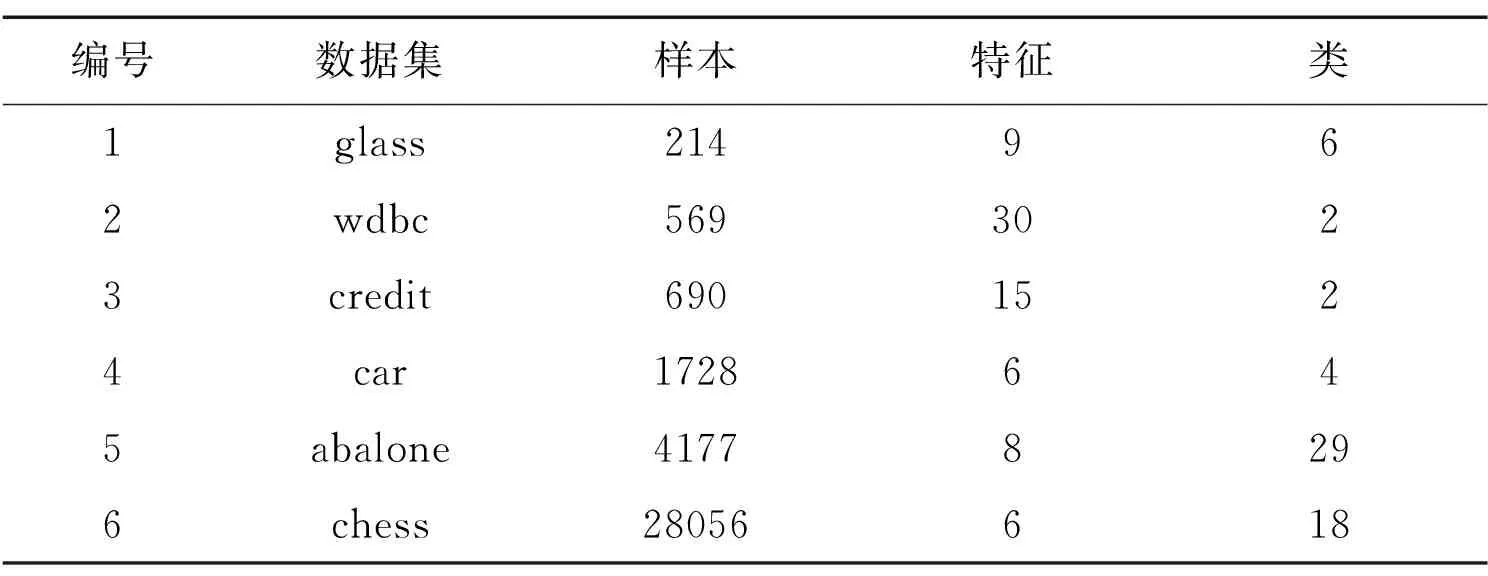
3.1 实验设置
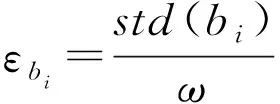
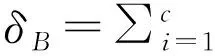
Table4ThesettingofthecostmatrixofclassCli
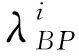
3.2 实验结果分析
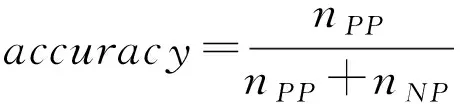
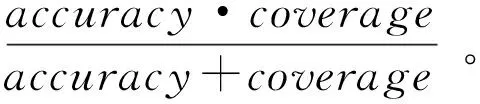
Table 5 Comparison of the accuracy of the classification results of each classification algorithm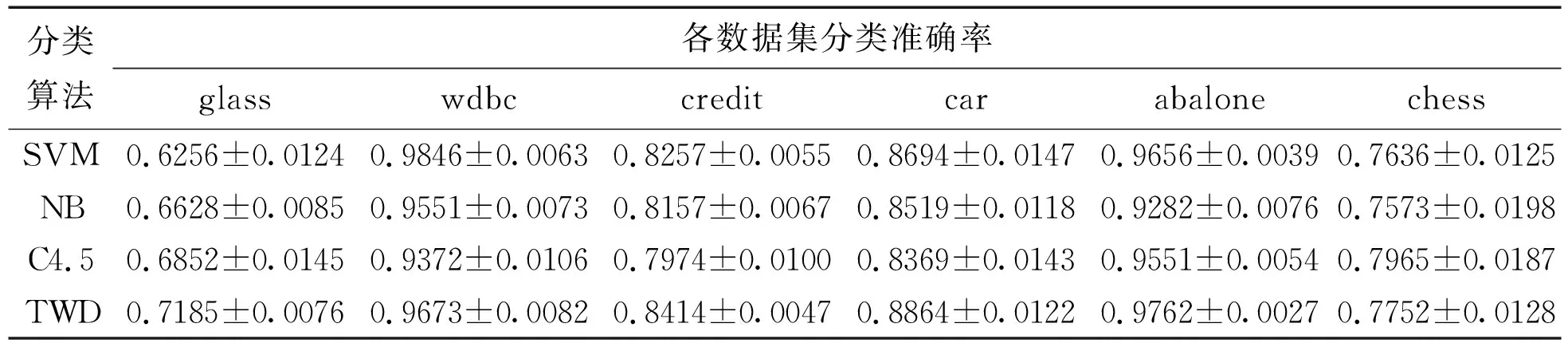
Table 6 F-measure comparison of classification results of each classification algorithm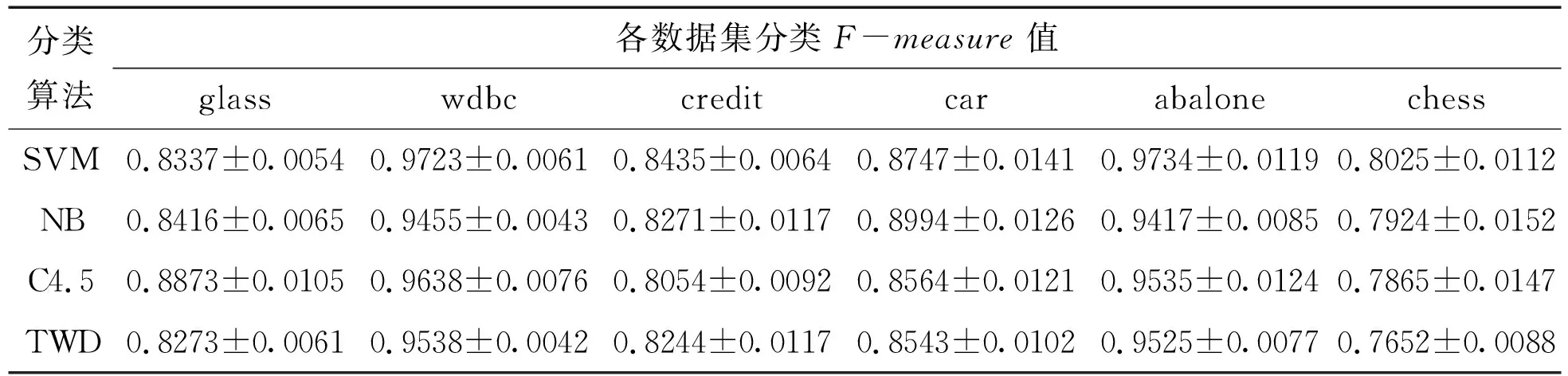
Table 7 Comparison of misclassification cost for classification results of each classification algorithm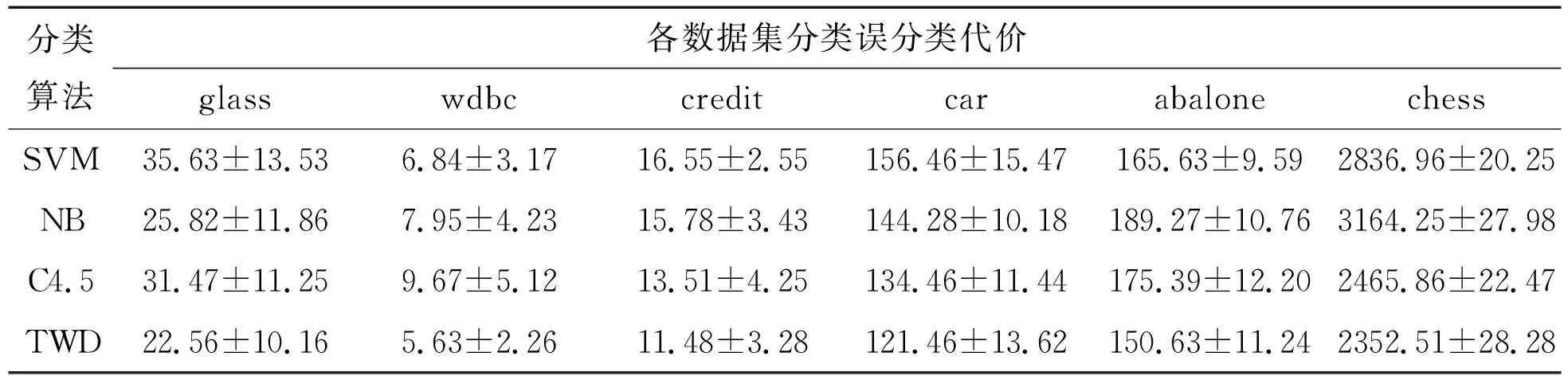
4 总结

