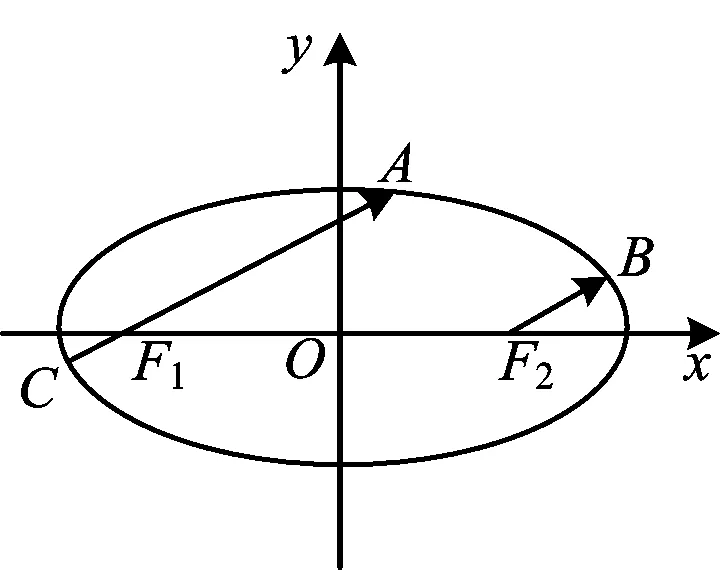
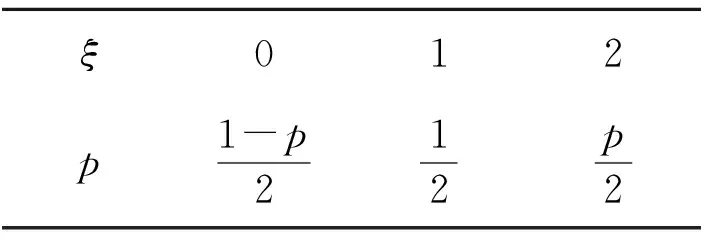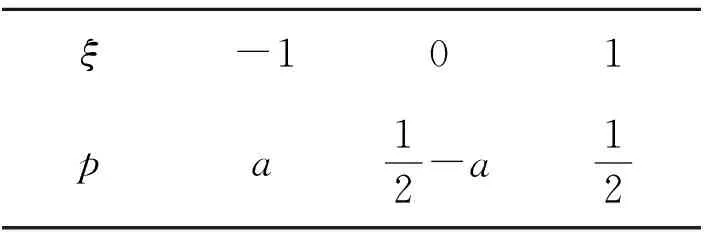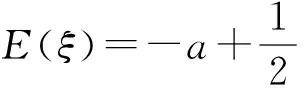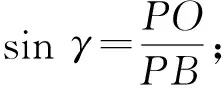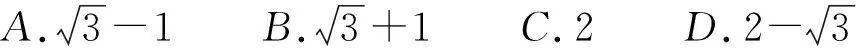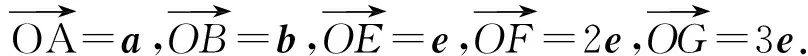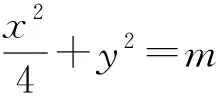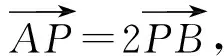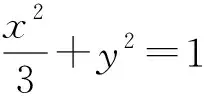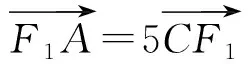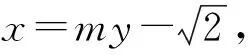试题本是同根生 复习何需题海战*——2018年数学高考浙江卷同源题赏析

●

(游埠中学,浙江 兰溪 321106)

浙江省从2004年开始自主命题至今已有15年，形成了鲜明的“浙派”命题风格：低起点、宽入口、多层次、区分好.2018年是浙江省文理合卷的第二年，试题整体平稳，考查内容全面而深刻，重视基础知识，追求数学本质，试题简约但不简单.

笔者仔细研读2018年浙江省数学高考真题，发现有许多试题与以前的真题似曾相识，或命题形式相同，或解法一致，或考查的数学本质相同，故收集一部分题目撰写本文，与同行一起交流.

题源1函数奇偶性.

例1函数y=2|x|sin 2x的图像是

( )

A. B. C. D.

(2018年浙江省数学高考试题第5题)

( )

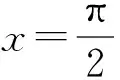
A. B. C. D.

(2015年浙江省数学高考文科试题第5题)

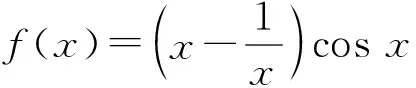
评注这两道试题在命题方式及考查内容上高度一致，考查学生对函数性质和图像的掌握情况，属于简单题.

题源2方差概念的理解.

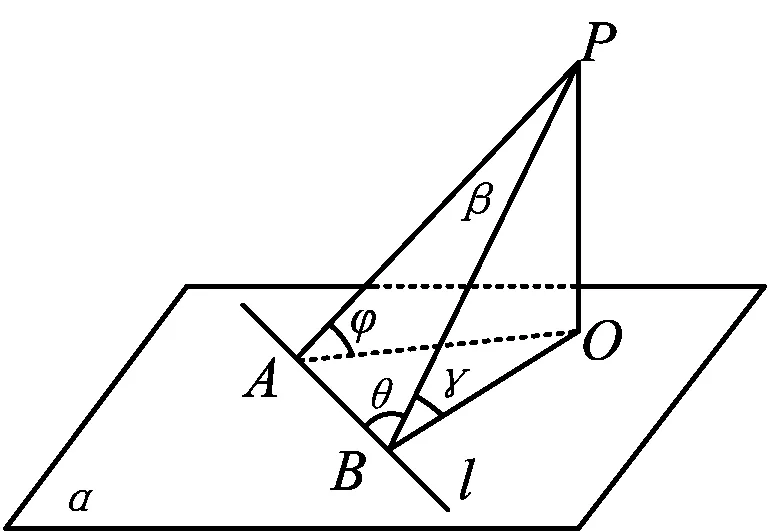
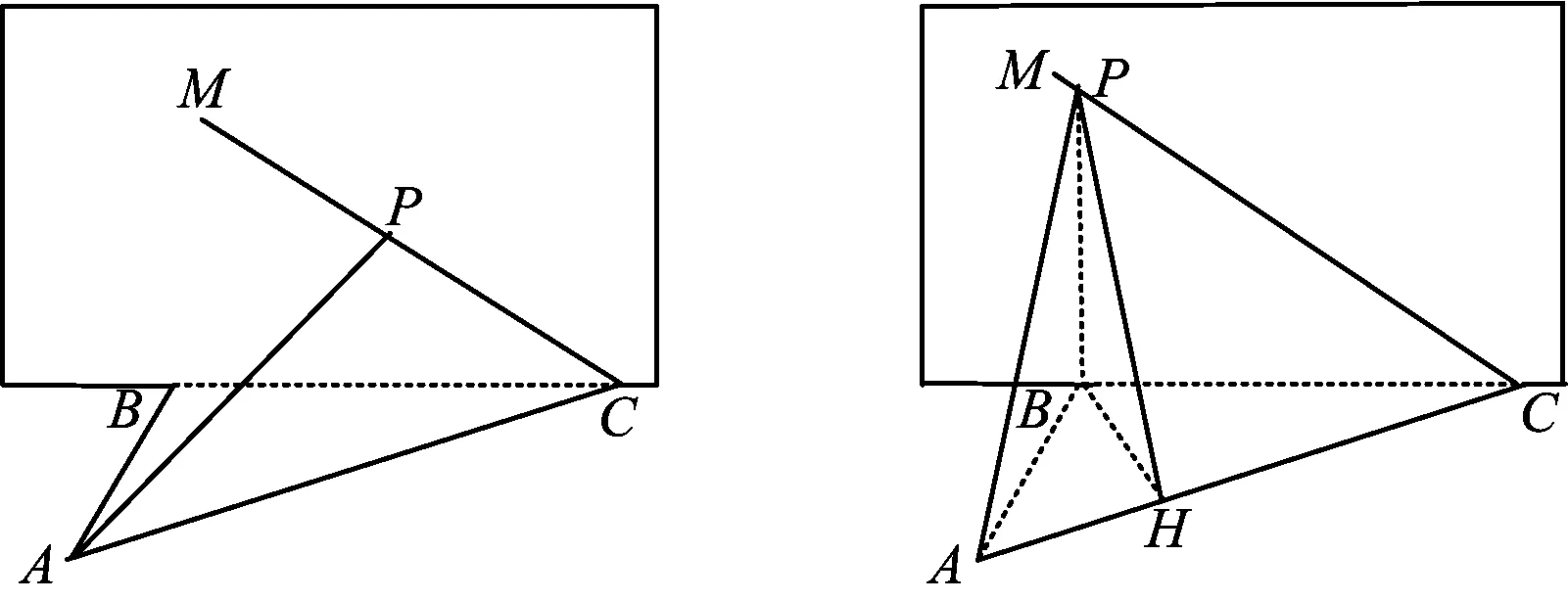
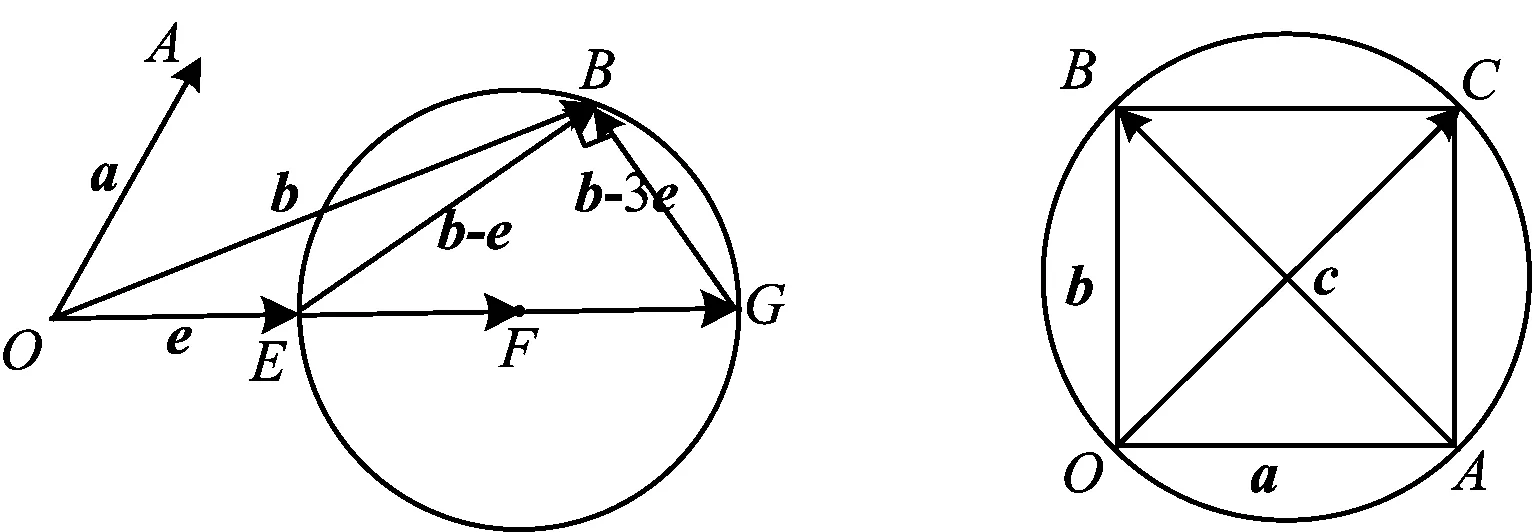
例3设0

( )

A.D(ξ)减小 B.D(ξ)增大

C.D(ξ)先减小后增大

D.D(ξ)先增大后减小

(2018年浙江省数学高考试题第7题)

分析当p在(0,1)内增大时，随机变量ξ的取值从集中到分散再集中，因此D(ξ)先增大后减小，正确答案为D.

表2 随机变量ξ的分布列

当a增大时，

( )

A.E(ξ)增大，D(ξ)增大

B.E(ξ)减小，D(ξ)增大

C.E(ξ)增大，D(ξ)减小

D.E(ξ)减小，D(ξ)减小

(2016年12月浙江省数学高考统测卷第7题)

题源3最小角定理与最大角原理.

最小角定理平面的斜线与其射影所成的角(线面角)，是这条斜线和这个平面内任一条直线所成角中的最小角.

最大角原理[1]二面角的一个半平面内的直线与另一个半平面所成的角不大于二面角的平面角.

图1

证明如图1，P是平面α外一点，PO⊥α，O是垂足，直线l⊂α，点P与直线l所确定的平面为β，点B∈l，AO⊥l.

例5已知四棱锥S-ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点).设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S-AB-C的平面角为θ3，则

( )

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

(2018年浙江省数学高考试题第8题)

分析抓住线面角最小，直接秒杀得到正确答案为D.

例6如图2，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB=15 cm，AC=25 cm，∠BCM=30°，则tanθ的最大值是______(仰角θ为直线AP与平面ABC所成的角).

(2014年浙江省数学高考理科试题第17题)

图2 图3

评注这又是一道挖掘概念背后本质的好题目.在一个题目中同时考查线线角、线面角、二面角，体现了命题组的别具匠心，更需要考生透过试题认识其本质.

图4

让我们再来重温2016年12月的浙江省数学统测卷第9题：如图4，已知三棱锥D-ABC，记二面角C-AB-D的平面角是θ， 直线DA与平面ABC所成的角是θ1，直线DA与BC所成的角是θ2，则

( )

A．θ≥θ1B．θ≤θ1C．θ≥θ2D．θ≤θ2

根据最大角原理，立即可得正确答案为A.

题源4“圆”来如此.

( )

(2018年浙江省数学高考试题第9题)

分析因为b2-4e·b+3=b2-4e·b+3e2=0，所以

(b-3e)·(b-e)=0.

图5 图6

例8已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是

( )

(2008年浙江省数学高考理科试题第9题)

评注例7在例8的基础上进行了深化，考查了圆的直径式方程的向量形式，充分发挥了向量的双重身份(兼具代数性质与几何性质).根据

|a+b|=|a-b|⟺a⊥b，

由(b-3e)·(b-e)=0进一步可得

|b-2e|=1，

这就是圆的标准方程的向量形式.同样地，由(a-c)·(b-c)=0可得

结合绝对值三角不等式，可知

从而

对于函数f(x)=ex，其在x=0处的泰勒展开式为

当0

两边取对数，得

综上可得

事实上，上述不等式可以加强为

利用导数可以证明，限于篇幅不再叙述,可参看文献[2]．

例9已知a1，a2，a3，a4成等比数列，且a1+a2+a3+a4=ln(a1+a2+a3).若a1>1，则

( )

A.a1a3，a2

C.a1a4D.a1>a3，a2>a4

(2018年浙江省数学高考试题第10题)

分析由题意得

a1+a2+a3+a4= ln(a1+a2+a3)≤

a1+a2+a3-1，

从而

a4≤-1.

又a1>1，得q<0.若q≤-1，则

a1+a2+a3+a4=a1(1+q)(1+q2)≤0，

a1+a2+a3=a1(1+q+q2)≥a1>1，

此时

ln(a1+a2+a3)>0，

与题设矛盾,故-1

a1-a3=a1(1-q2)>0，

a2-a4=a1q(1-q2)<0.

正确答案为B.

例10已知数列{xn}满足x1=1，xn=xn+1+ln(1+xn+1)(其中n∈N*).证明：当n∈N*时，

1) 0

(2017年浙江省数学高考试题第22题)

又xn=xn+1+ln(1+xn+1)≤2xn+1，得

即

第3)小题的左半部分，同样地,由xn=xn+1+ln(1+xn+1)≤2xn+1,得

题源6韦达定理与运算求解.

(2018年浙江省数学高考试题第17题)

分析设A(x1,y1)，B(x2,y2).当直线AB的斜率不存在时，x2=0，m=9.当直线AB的斜率存在时，设直线AB的方程为y=kx+1，代入椭圆方程得

(1+4k2)x2+8kx+4-4m=0,

由题意

Δ=4mk2+m-1>0,

根据韦达定理得

x1=-2x2,

(3)

把式(3)代入式(1)，得

即

解得m=5，经检验符合题意.

(2011年浙江省数学高考理科试题第17题)

图7

分析如图7，过点F1作F1C∥F2B交椭圆于点C，则根据对称性易知

y1=-5y2.

(4)

由韦达定理得

联立式(4)～(6)解得y1=±1.故点A的坐标为(0,±1).

评注从上述解题过程看到，例11其实是例12的变式.从原先的定值问题演变为最值问题，考查了解析几何的核心方法——坐标法，考查了学生的运算求解能力，属于难题.

“年年岁岁题相似，岁岁年年意不同”，浙江卷以基础知识和基本技能的考查为载体，体现数学思想方法，体现能力立意，重在对数学本质的理解，反对题海战术和解题套路.这就启示我们在高三复习时，应该科学安排，回归基础，钻研真题，重视解题的通性通法，这样才能在高考时拔得头筹.