数学教学要体现学生的再创造过程*——以“两条直线的平行和垂直”教学为例

●

(常州市第二中学,江苏 常州 213003)

数学学习是一种再创造的过程.弗赖登塔尔说过：“学习数学的唯一正确方法是实行‘再创造’，也就是由学生本人把要学的东西自己去发现或者创造出来.教师的任务是引导和帮助学生去进行这种再创造的工作，而不是把现成的知识灌输给学生.”[1]如何有效引导和帮助学生实现再创造就成了教师首当其冲要解决的问题，本文结合笔者开设的苏教版高中《数学(必修2)》中“两条直线的平行和垂直”公开课为例，就如何在数学教学中体现再创造的过程，谈谈自己的实践和思考.

1 教材分析

本节内容选自苏教版高中《数学(必修2)》第2.1节，学生在此之前已经学习了用坐标表示平面几何基本图形中的点、线,用代数对象的有序实数对和方程表示几何对象的点、线,在此基础上,进一步学习利用代数方程精确研究线与线之间的位置关系.解析几何的本质是用代数方法研究几何问题，核心思想是坐标法思想[2].因此，在教学中要突出坐标法思想，即通过建立坐标系，把几何对象转化为代数对象，把几何问题转化为代数问题，利用代数的工具、方法研究并获得结论，然后再解释几何现象.

2 学情分析

平面几何是学生初中阶段已经学习过的内容，学生已经掌握了判断线线位置关系的方法，这可以为新的判断方法提供知识基础.本节课蕴含了数形结合、分类讨论、坐标法等重要的思想方法，对思维严谨性要求较高.学生易于掌握线线平行和垂直的斜率关系，但是对于位置关系中的重合和斜率不存在的情况容易忽视.

3 教学目标

结合教材分析和学情分析，设计教学目标如下：

1)掌握用斜率判定两条直线平行和垂直的方法，能够判断简单的线线位置关系；

2)让学生进一步感受坐标法思想在研究几何问题中的重要作用；

3)通过分类讨论和数形结合思想方法的运用，培养学生思维的严谨性.

教学重点：掌握两条直线平行和垂直时斜率的关系.

教学难点：线线平行和垂直需要考虑直线重合和斜率不存在的情况.

4 教学过程设计

4.1 课题引入

问题1前面已经学习了利用坐标系把平面几何中的基本图形点、线转为代数对象的有序实数对、方程进行表示.研究完基本图形后，可以继续利用坐标系研究与点、线有关的哪些内容？

生1：可以研究点与线、线与线的位置关系.

设计意图学生习惯了教师给出学习内容，让学生自己提出课题，这对学生思维有一定的挑战.在教学中，笔者引导学生回顾平面几何的学习内容，学生能够提出课题，变被动学习为主动研究，从而充分调动学生学习的兴趣和积极性.

师：这些都是接下来要研究的内容，本节课我们首先研究线与线的位置关系.直线l1,l2的位置关系有哪些？

生2：平行、相交、重合.

师：本节课我们主要研究线线平行和垂直.

图1

问题2观察图1，直线l1,l2的位置关系是什么？

生3：平行.

师：你是怎么知道它们平行的？

生3：看起来平行.

师：看起来平行一定平行吗？

生3：不一定，根据直线的无限延伸性，看起来平行，也有可能相交.

4.2 建构概念

师：几何直观不够精确，不能作为判断平行的依据，你能利用所学的知识去判断直线平行吗？

设计意图问题2是本节课设计的问题情境，这里给出的两条直线不是平行的，形虽然直观，但是容易有误差.如何说明直线平行，把学生推入思维的困境，他们就会思考如何才能准确判断直线平行，代数方法研究就有了必要性.

生4：利用同位角、内错角、同旁内角来判断直线平行.

师：你怎么利用这些知识来判断？

生4：在图1中画一条直线与这两条直线相交.

师：联系我们前面刚学的知识，这条线可以是哪条线？

生4：x轴.

师：这时直线与x轴正方向所成角也称为倾斜角，倾斜角是对直线倾斜程度的刻画，还有什么量也可以刻画？

生4：斜率.

师：如何利用倾斜角和斜率来判断直线平行？

生4：首先要建立直角坐标系.

设计意图教学中要突出坐标法的思想，坐标法的第一步就是建立坐标系.“为什么要建系，如何想到要建系”这是非常有价值的教学点.通过设问，学生自己感受建立坐标系的必要性，从而渗透坐标法思想在解决几何问题中的重要作用.

图2

问题3观察图2，当直线l1,l2平行时，它们的倾斜角有什么关系？

生5：倾斜角相等.

师：为什么？

生5：因为倾斜角就是同位角，两直线平行，同位角相等.

问题4当直线l1,l2平行时，它们的斜率有什么关系呢？

生6：斜率相等.

师：能不能说“若直线l1,l2平行，则斜率相等”？

生6：当斜率存在，两条直线平行，则斜率相等.

师：直线l1,l2平行可以推出斜率相等，反过来，直线l1,l2斜率相等可以推出平行吗？

生7：需要指出直线l1,l2不重合.

师：当直线l1,l2斜率不存在时，且l1,l2不重合，则l1∥l2.

总结当直线l1,l2斜率存在时，有

当直线l1,l2斜率不存在，且l1,l2不重合时，l1∥l2.

师：回到问题情境，请利用所学知识判断图1中的直线是否平行？

生8：首先需要在两条直线上各取两个点，然后度量坐标，再计算斜率，判断斜率是否相等就可以判断直线的位置关系.

图3

学生叙述方法，教师利用几何画板软件进行操作，如图3，发现斜率不相等，则直线l1,l2不平行.然后对直线l1,l2进行延伸，找到两条直线的交点，加强学生对代数方法研究几何问题的精确性的认同.

师：利用坐标系从代数角度可以精确研究直线的平行，光从形的角度容易出现误差，华罗庚先生曾说过：“形少数时难入微”，就是这个意思.

通过回顾问题情境，教师向学生展示坐标法思想，具体如下：

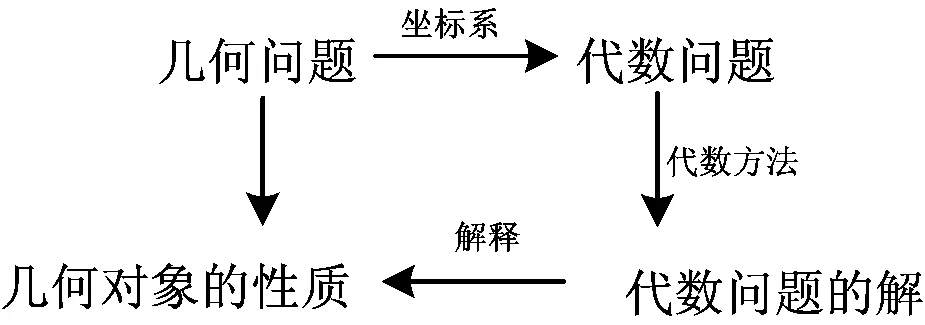
问题5观察图4和图5中的两组直线l1，l2，它们是什么位置关系？

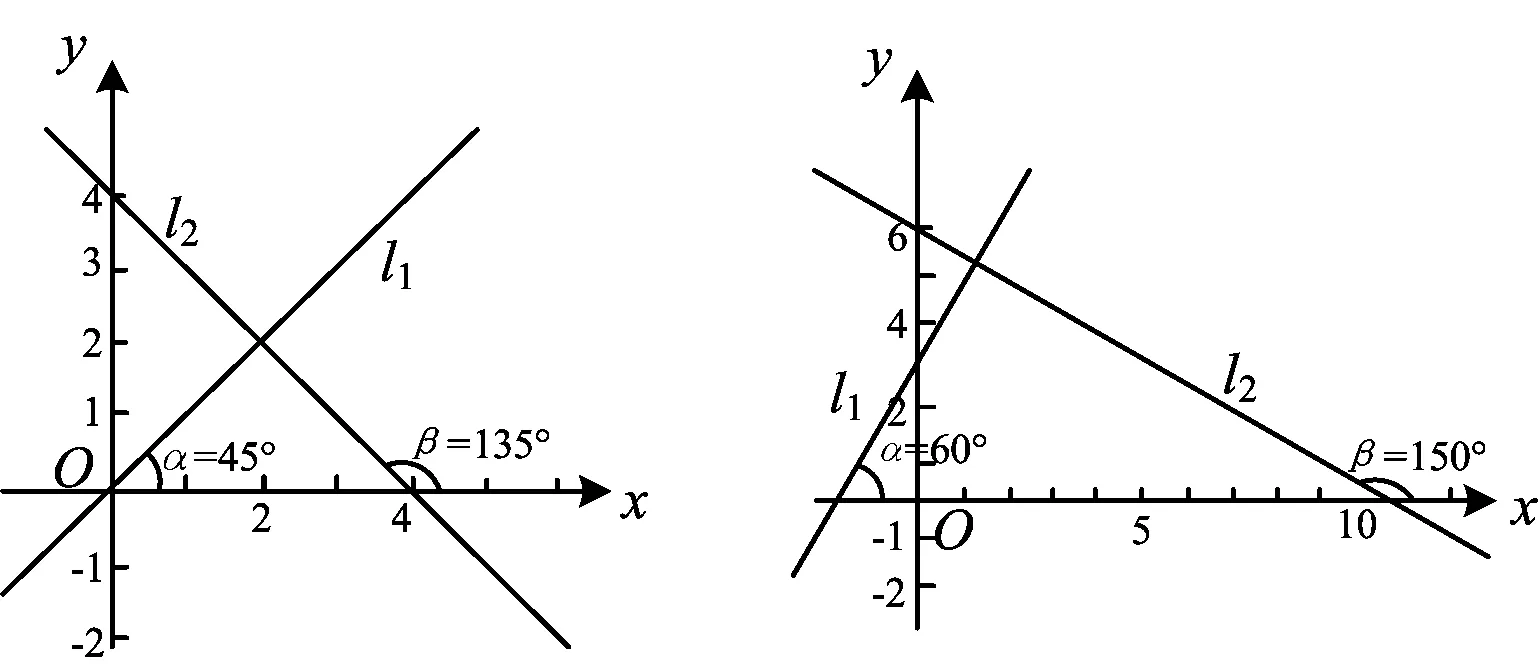
图4 图5

图6

教师首先展示图4和图5，给出垂直时倾斜角的关系：β=α+90°，0°<α<90°，90°<β<180°；继而让学生猜想一般情况下线线垂直的斜率关系(如图6)，猜想：l1⊥l2⟹k1k2=-1.

设计意图学生难以直接发现当直线l1⊥l2时的斜率关系，这里采用从特殊到一般的方法，让学生通过具体实例，猜想k1k2=-1；再让直线动起来，发现当直线l1⊥l2时，始终有k1k2=-1，从而验证猜想的正确性.

师：通过操作能否说明“若直线l1⊥l2，则k1k2=-1”？

生(众)：不可以，需要给出证明.

师：请利用条件“k=tanα,其中α≠90°，β=α+90°，0°<α<90°”给出证明.

设计意图这是本节课的一个难点，学生可以类比利用直线倾斜角的等式关系，推导出斜率关系，教师可以放手让学生去推导.

学生得到：

k1k2= tanαtanβ=tanαtan(α+90°)=

思考当k1k2=-1时，直线l1,l2垂直吗？你能将上述的发现总结一下吗？

设计意图给学生总结的机会，让学生自己提出需要注意斜率不存在的情况，强化学生的分类讨论意识.

总结设直线l1,l2的斜率分别为k1，k2，当k1，k2都存在时，l1⊥l2⟺k1k2=-1；当k1不存在、k2=0时，l1⊥l2.

4.3 课堂练习

例1已知直线l1经过点(-1,-2),(1,2)，判断下列直线与l1的位置关系.

1)直线l2经过点(3,1),(5,5)；

2)直线l3经过点(-2,1),(2,-1)；

3)直线l4经过点(2,4),(3,6).

答案1)l1∥l2；2)l1⊥l2；3)重合.

设计意图让学生运用所学知识判断直线之间的位置关系，强化对公式的掌握.第3)小题的设计是让学生了解画图的重要性，利用斜率判断平行无法排除重合的情况.解析几何本质上是用代数方法研究图形的几何性质，解析几何兼具“形”“数”两个方面的特点，画出图形，利用图形的几何直观能够让我们预判直线的位置关系，然后再用代数方法加以验证，这正是数形结合思想的体现.

例2已知△ABC的顶点为A(2,-1),B(-1,1)，C(3,7),

1)试判断△ABC的形状；

2)求过点B与AC平行的直线l1的方程；

3)求过点B与AC垂直的直线l2的方程.

答案1)直角三角形；2) 8x-y+9=0；3)x+8y-7=0.

设计意图通过例2的教学，继续强化学生解决解析几何问题的画图意识.

4.4 课堂总结

问题6本节课你有哪些收获，请从知识层面和思想方法层面进行总结.

问题7接下来，我们还可以继续利用坐标系研究平面几何的哪些内容？

设计意图总结反思是一节课的提升，是学生收获战利品的时候，十分重要，不能走形式，要给予学生必要的时间总结内化.问题7的提出，让知识学习具有系统性和连续性，从而激发学生继续探究的欲望.

5 教学反思

1)充分了解学生已有的认知结构，是再创造的前提.

2)创设有效问题情境，是再创造的关键.

问题情境是一节课至关重要的部分，好的开始是成功的一半.好的问题情境能够一下子吸引学生的兴趣和注意力.笔者在最初进行教学设计时发现教材给出的情境设计很简单，直接给出了直线平行和垂直的斜率关系，然后加以证明就结束了.笔者在查阅相关资料后，发现本节课主要有两种问题情境的设计模式：一类给出建筑物平行和垂直的实例，然后引入课题；另一类是给出几组具体的直线平行和垂直的方程，让学生画图发现特殊的位置关系，再一般化研究.前者设计的问题情境在课题引出后就失去了价值，后者则过于平淡，两者都难以有效体现再创造的过程.

为什么初中阶段已经学习过的直线平行和垂直在高中阶段还要再学习？学生是存在困惑的，抓住这一点，笔者给出了一组看似平行实则相交的直线让学生去判断位置关系，学生认为平行，却没有合适的方法去证明，就会产生认知冲突，就有自发学习新知的内在需求.问题情境的设计能有效体现形的直观但容易有偏差，为了弥补形的不足，需要建立坐标系，利用代数方法的精确研究直线的位置关系，使得教学过程顺其自然.教师带着疑惑，引导学生自主探究出直线平行的斜率关系，再回到问题情境，让学生应用所学的知识去解决问题情境提出的问题.这样的设计让问题情境不再只是点缀，而是使学生浸润于问题情境中，通过自主思考，探索解决问题的方法，学生能够在学习中获得成就感.

3)大胆留白，是再创造的保障.

学生是数学学习的主人，再好的教学设计，如果学生的思维没有参与，那么将会事倍功半.教师往往替学生想的太多、包办的太多，使得教学设计过于“饱满”，留给学生思考的余地很少，学生的思维能力很难得到提高发展.教师要做的就是设计具有启发性和目的性的好问题，在教学中大胆留白，让学生去思考探索，去展示交流想法，把学生充分卷进课堂中来，这样才能真正体现学生的主体性地位，实现数学学习的再创造.