广义可压缩杠杆方程的精确行波解
,
(浙江理工大学理学院,杭州 310018)
0 引 言
非线性方程是描述自然现象的一种重要数学模型,对其行波解的研究是近年来非线性动力系统中的热点之一。为了研究非线性方程的行波解,人们已经提出了一些行之有效的方法,其中动力系统研究方法[1-2]已经很好地应用于非线性方程行波解的研究中。本文主要运用动力系统的分支方法研究下列广义可压缩杠杆方程[3-4]:
(1)
其中:g是给定的C∞函数,γ是与材料常数和杆的感应力有关的常数。当γ=1,g(u)=3u2时,方程(1)为Camassa-Holm方程[5]:
ut-uxxt+3uux+kux=2uxuxx+uuxxx
(2)
方程(2)具有双哈密顿结构、可积性、有无穷多个守恒律,且已经得到了方程(2)的周期解、孤波解、Peakon等[6-7]。当g(u)=3u2,γ∈(-29.4760,3.4174)时,方程(1)为超弹性杆波方程[5]。当γ=0,g(u)=3u2时,方程(1)为Benjamin-Bona-Machony方程[3]。本文主要研究当γ=1,g(u)=3au2+2ku(a≠0)时,方程(1)的行波解。
为了研究方程(1)的行波解,首先令u(x,t)=u(ξ),ξ=x-ct,并代入方程(1),再关于ξ积分一次并取积分常数为0可得:
(3)
本文通过研究常微分方程(3)参数a,c和k的分支和相图将得到方程(1)的各类行波解。
1 行波系统的分支与相图
令u′=v,若u≠c,方程(3)可转化为平面系统
(4)
u=c是系统(4)的奇直线。时间尺度变换dξ=(u-c)dη将系统(4)化为
(5)
其首次积分为
H(u,v)=(c-k-au)u2+(u-c)v2
(6)
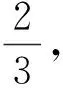
分支曲线把参数平面(c,k)分为八个区域:
D1={(c,k)|c>k>0},
D2={(c,k)|k>c>0},
D5={(c,k)|c D6={(c,k)|k c) 当(c,k)∈D3∪D7时,系统(5)有鞍点(0,0)和(u1,0)。 f) 当(c,k)∈C3时,系统(5)有尖点(c,0)和鞍点(0,0)。 系统(5)的相图见图1。 分支曲线把参数平面(c,k)分为八个区域: 引理2当a<0时,系统(5)在每个参数区域和分支集上的奇点类型如下所示: a) 当(c,k)∈D1∪D4∪D5∪D8∪C4时,系统(5)有鞍点(0,0)和中心(u1,0)。 b) 当(c,k)∈D2∪D6时,系统(5)有鞍点(u1,0)为鞍点和中心(0,0)。 d) 当(c,k)∈C1时,系统(5)仅有一个尖点(0,0)。 f) 当(c,k)∈C3时,系统(5)有尖点(c,0)和中心(0,0)。 系统(5)的相图见图2。 图1 当时,系统(5)的相图 图2 当a<0时,系统(5)的相图 注意u=c为系统(4)的奇直线。众所周知,与奇直线不相交的轨线对应于方程的光滑行波解。在物理中令人感兴趣的光滑行波解一般是周期波、孤波、扭波或反扭波,它们分别对应于相图中的周期轨、同宿轨和异宿轨[1]。系统(5)的轨道由下列方程确定 (c-k-au)u2+(u-c)v2=h (7) 当u≠c时,方程(7)可以写成 (8) I(u,u0,c,k,h)=±ξ (9) 是方程(1)的隐式解。 a) 当(c,k)∈D1((c,k)∈D5)且h=H(u0,0)时,若u0∈(u1,u2)(u0∈(u2,u1)),式(9)确定了方程(1)的周期行波解;若u0=u2,则确定了方程(1)的孤波解。 c) 当(c,k)∈D4∪C4(c<0)((c,k)∈D8∪C4(c>0))且h=H(u0,0)时,若u0∈(c,u1)(u0∈(u1,c)),式(9)确定了方程(1)的周期行波解。 定理2当a<0时,方程(1)有如下的有界光滑行波解: a) 当(c,k)∈D1∪D8∪C4(c>0)((c,k)∈D4∪D5∪C4(c<0))和h=H(u0,0)时,若u0∈(u2,u1)(u0∈(u1,u2)),式(9)确定了方程(1)的周期行波解;若u0=u2,则确定了方程(1)的孤波解。 c) 当(c,k)∈D3((c,k)∈D7)和h=H(u0,0)时,若u0∈(0,c)∪(c,u1)(u0∈(u1,c)∪(c,0)),则式(9)确定了方程(1)的两族周期行波解。 按照寓管理于服务,转变管理方式,加快转变政府职能,该放的放掉、该管的管好,突出加强涉水社会事务跟踪和趋势研判,准确把握水利舆情动态,做到前移关口、重心下放,从源头上预防问题、解决问题,把更多资源投入到基层,让基层有权管事、有人做事、有钱办事。 e) 当(c,k)∈C3和h=H(u0,0)时,若u0∈(0,c),式(9)确定了方程(1)的周期行波解。 行波系统的与奇直线相交的有界轨道对应于奇异行波解。当u≠c时,方程(8)可以写成 (10) a) 当(c,k)∈D4且h=H(u0,0)时,若u0∈(u-,0),则 (11) 是方程(1)的周期cuspon;若u0=u-且h=H(u0,0),则式(11)是方程(1)的周期peakon。 b) 当(c,k)∈D8且h=H(u0,0)时,若u0∈(0,u+),则式(11)是方程(1)的周期cuspon;若u0=u+,则式(11)是方程(1)的周期peakon。 定理4若a<0,方程(1)有如下的有界行波解。 a) 当(c,k)∈D3∪D7且h=H(u0,0)时,若u0∈(-∞,u-)∪(u+,+∞),则式(11)是方程(1)的周期cuspon;若u0=u-(u0=u+),则式(11)是方程(3)的周期peakon。 b) 当(c,k)∈C2((c,k)∈C3)且h=H(u0,0)时,若u0=u+(u0=u-),则 (12) 是方程(1)的compacton。 动力系统研究方法是研究非线性方程行波解的重要方法之一。本文运用这一方法研究其分支并得到广义可压缩杠杆方程在各种不同参数条件下的有界行波解,包括光滑行波解和奇异行波解,其中光滑行波解有光滑孤波解和周期波解,奇异行波解有周期cuspon、周期peakon、孤立peakon和compacton。本文研究的是取积分常数为零的特殊情形,当积分常数不为零时,方程中将出现四个参数,从而研究其分支就更加困难,对于一般的情形是否可以得到方程新类型的行波解,将是下一步深入探讨的问题。
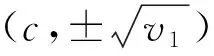
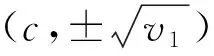

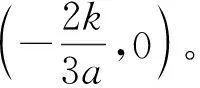
1.2 a<0的情形



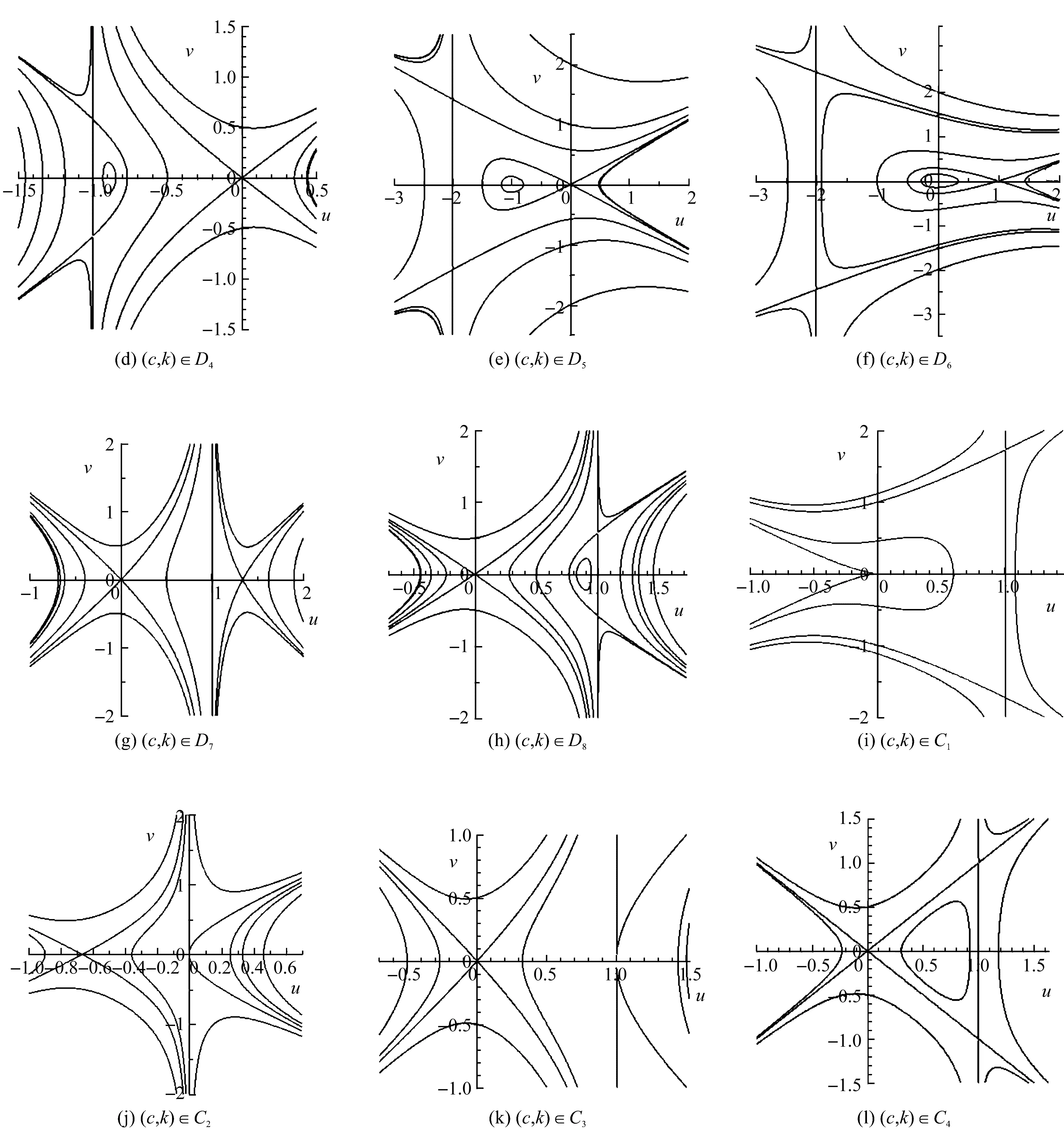
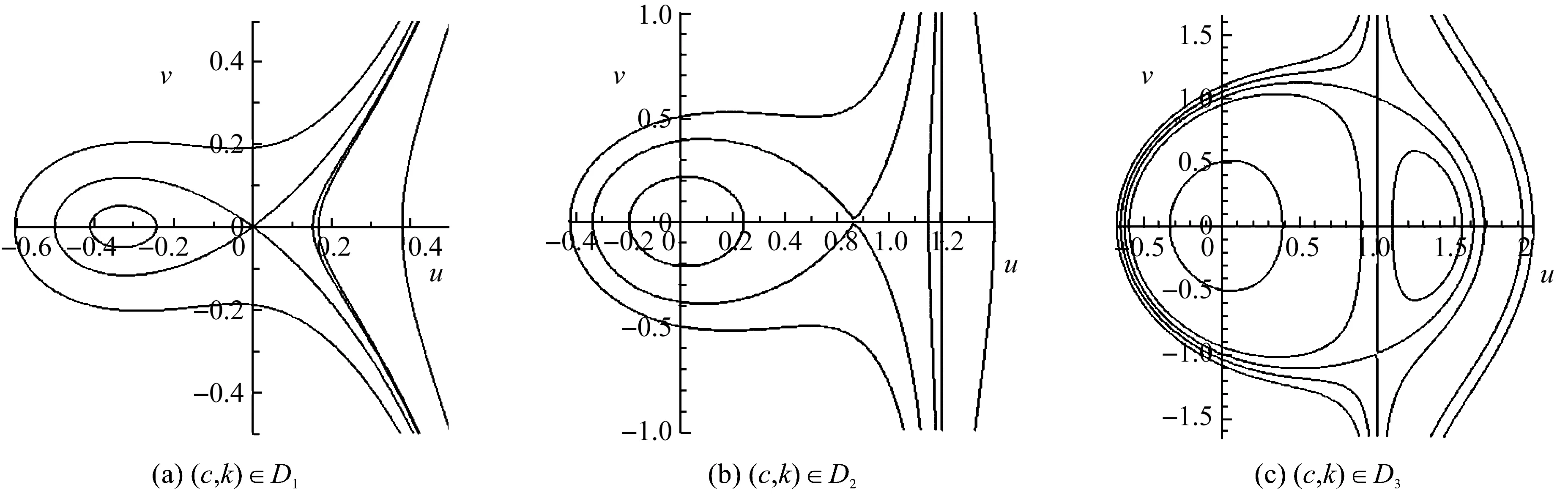

2 方程(1)的有界光滑行波解
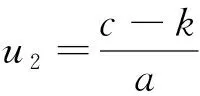

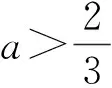

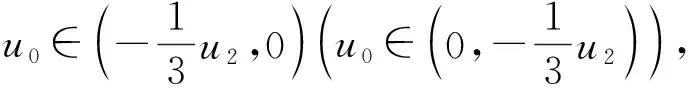
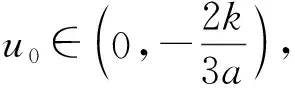
3 方程(1)的奇异行波解

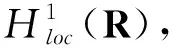



4 结 语

