含有2的幂次的Euler和的研究

，

(浙江理工大学理学院,杭州 310018)

0 引 言

广义调和数的定义为

当p=1时为经典的调和数，用Hn表示。

设p1,p2,…,pm为正整数，且p1≤p2≤…≤pm，x∈[-1,1)，记

称p1+…+pm+q为Sp1p2…pm,q(x)的权。为方便起见，类似整数分拆的记法，将重复的数字用幂的形式来表示，例如，

在Sp1p2…pm,q(x)中令x=1，就得到经典的Euler和Sp1p2…pm,q。Berndt[1]指出，Euler和的研究起源于1742年，在与Goldbach的通信中，Euler首先考虑了线性和

并得出很多结果。例如，Euler指出当q≥2时，S1,q可以用zeta值表示：

本文主要研究含有2n的Euler和，并通过生成函数及特殊函数积分系统地计算出一些低阶的含有2n的Euler和的值。

1 一些引理

引理1当k≥1时，第一类无符号Stirling数满足如下生成函数：

(1)

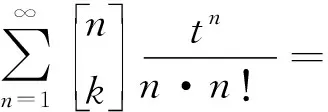
Lij(1-t)+ζ(k+1)

(2)

引理1中(1)即为第一类无符号Stirling数的指数型生成函数。Wang等[7]在(1)的基础上通过积分进一步得到生成函数(2)。利用第一类无符号Stirling数与Bell多项式的关系[7]：

可以将(1)和(2)改写为

(3)

(4)

(5)

(6)

由(5)和(6)可以进一步得到含有2n的Euler和的关系式。

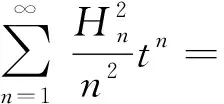
ln2(1-t)Li2(1-t)+2ln(1-t)Li3(1-t)-

2Li4(1-t)+2ζ(4)

(7)

(8)

(9)

再令r取特殊值也可得到含有2n的Euler和的关系式。

最后，Choi等[9]利用Kummer求和公式得到两个含有2n的无穷级数的表达式。

引理3设k≥0为整数，则

(10)

(11)

其中pk满足以下递推关系：

2 权2，3，4的含有2n的Euler和的计算

利用上述引理可以系统地得到权2，3，4的含有2n的Euler和的值。

定理1权为2，3的4个含有2n的Euler和可以用zeta值表示。

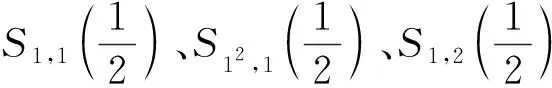
解以上三个线性方程构成的方程组可以得到权3的所有Euler和：

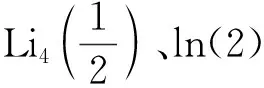
在(5)中令k=4，可以得到

类似地，在(6)和(10)中令k=3，在(11)中令k=2可以得到另外3个方程。

解以上线性方程组可以得到权4的所有Euler和：

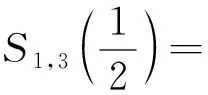
3 含有2n的Euler和与交错Euler和的关系

Xu[12]通过以下积分定义了序列(Yk(n))：

该序列满足如下递推公式：

利用序列(Yk(n))可以建立含有2n的Euler和与交错Euler和的关系。

定理3对于正整数k，有

= (-1)m+1m!ζ(m+1)ln(2)+

(12)

另一方面，直接做变量替换x→1-t可得

ln(2)·(-1)m+1m!ζm+1

(13)

结合(12)和(13)可以得到结果。

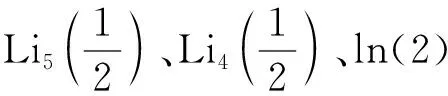
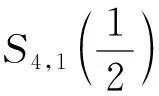
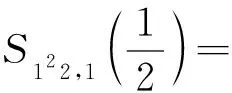
4 结 论

本文利用生成函数的方法得到权2，3，4的所有含有2n的Euler和，并利用特殊函数积分的方法建立含有2n的Euler和与交错Euler和的关系，由此计算出两个权5的含有2n的Euler和。笔者将在后续的研究中利用生成函数、特殊函数积分，建立更多的含有2n的Euler和与交错Euler和的关系，得到足够多的方程，由此求解出所有权5、6的含有2n的Euler和。