带有饱和发生率和线性饱和治疗函数的SIS模型的动力学研究
,
(浙江理工大学理学院,杭州 310018)
0 引 言
为了发现传染病的传染规律并有效地对传染病进行控制,许多学者致力于传染病模型动力学问题的研究。基本再生数R0是传染病模型中决定疾病是否消失的一个重要依据,R0>1意味着疾病持续,R0≤1表示疾病消失。在经典传染病模型中,从无病平衡点到地方病平衡点的分支是向前的。但当后向分支发生时,即使R0<1,模型仍存在多个地方病平衡点,因此根据R0是否小于1不能判断疾病是否灭绝。
1927年,Kermack等[1]研究了著名的SIRS传染病模型,该模型包括易感者(Susceptible polulation,S)、感染者(Infected population,I)以及恢复者(Recovered population,R)。由于发生率函数和治疗函数反映的分别是传染病的传染规律和治疗规律,因此发生率函数和治疗函数是影响传染病模型动力学行为的两大重要因素。例如双线性发生率函数[2-3],当治疗率较小时,后向分支发生且存在稳定的地方病平衡点。随着研究的深入,研究者们发现,这种发生率函数不能精确表达疾病的传播特点。这是因为当感染者数量增大时发生率函数并不像双线性发生率函数那样呈线性增加,而是需要适当的函数形式和适当的参数限制感染者与易感者之间的无限接触。由此,研究者们提出了饱和发生率函数[4-8],饱和发生率函数显然比双线性发生率函数更合理。此后,大量非线性发生率函数和一般发生率函数[9-11]相继提出。一般而言,非线性发生率函数比双线性发生率函数更能反映传染病的真实传染规律,同时能够产生更加丰富和复杂的动力学行为。
对传染病进行有效控制进而消灭的一种重要手段就是采取治疗。最早,Wang等[12]提出常数治疗,即对疾病存在固定的治疗能力。Wang[13]和吴琼等[5]进一步改进了常数治疗函数,采取线性饱和治疗函数,该治疗函数在没有达到最大值时,保持与感染者数量呈正比例关系,否则采取最大治疗能力。周康等[6]推广了该治疗函数,研究了具有常态预防能力的线性饱和治疗函数的SIR模型。此治疗函数的优点在于提出了常态下的预防,即在没有感染者被发现的情况下,医院对疾病保持有一定的治疗能力,这样更有利于对疾病的预防。除线性饱和治疗函数外,其他有关二次治疗函数和饱和治疗函数的相关研究参见文献[14-15]。
本文研究带有饱和发生率和线性饱和治疗函数的SIS模型,借助微分方程定性稳定性理论分析模型平衡点的存在性与稳定性,研究平衡点的共存性,进而确定该模型是否发生后向分支现象以及后向分支何时发生。
1 模型的建立
本文建立并研究的传染病模型为:
(1)
其中:
为治疗函数;m指饱和治疗率,m=kI0+β;β指常态下的正常预防能力,一般β>0;k为治愈率,一般k>0;A为人口补充率,一般A>0;λ为双线性发生率,一般λ>0;α代表由大量感染者出现或易感者行为变化对疾病发生率产生的抑制作用,一般α>0;d为自然死亡率,一般d>0;r为自然恢复率,一般r>0;ε为疾病致死率,一般ε>0;I0代表采取最大治疗能力时刻的感染者水平。文献[5]采用了线性饱和治疗函数h(I)=kI,也就是本文β=0的情况,该治疗函数没有常态预防能力。本文的工作将不具有常态下正常预防能力的治疗函数推广到了具有常态下正常预防能力的情形,研究结果更具一般性。
2 平衡点存在性
首先考虑模型(1)平衡点的存在性。显然,当感染者数量I=0时,模型(1)存在唯一的无病平衡点E0=(A/d,0)。地方病平衡点满足:
(2)
本文模型的基本再生数R0的表达公式为:
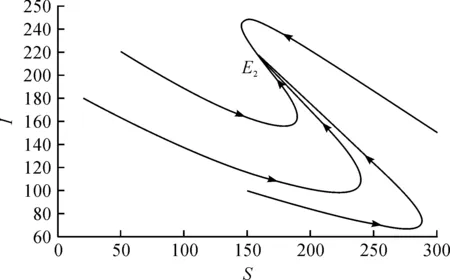
情形1:当0 (3) 将式(3)的两个方程相加得 将其代入式(3)的第二个方程并化简得: aI2+bI+c=0 (4) 其中: 故此一元二次方程可能有正解I1,I2: (5) 其中: Δ=b2-4ac=[d(d+ε+r+k)-λA+dβα]2-4dβ[λ(d+ε)+αd(d+ε+r+k)] (6) 从式(5)可以看出,当b≥0时,I1,I2均小于零。故只需考虑b<0的情况,而b<0等价于: (7) 又因为式(4)有解必须有Δ≥0,而Δ≥0等价于: (8) 或 先考虑I1>I0的情况,由于I1>I0等价于: b+2[λ(d+ε)+αd(d+ε+r+k)]I0<0, 故由该不等式可得: (9) (10) 故I1>I0等价于式(9)—(10)同时成立。因此,当R0≤P1或R0≥P2时,I1≤I0成立。 类似地,对I2>I0进行讨论,得到当P2 由于 定理1当R0≥P0时,对于模型(1)的两个地方性平衡点E1,E2, 情形2:当I>I0时,式(2)可化为: (11) 以下讨论式(11)的正的地方病平衡点,与讨论式(3)同理,设式(11)的两个正的地方病平衡点为E3,E4。 证明:由定理2的b)即可得到。 推论3模型(1)存在多个平衡点,但平衡点个数不超过4个。 推论4模型(1)同时存在4个平衡点是不可能出现的。 首先,讨论E1和E2的稳定性。令 可知式(2)的Jaccobi矩阵 定理3当R0<1时,无病平衡点E0是局部渐进稳定的;当R0>1时,E0是不稳定的。 定理4若模型(1)的地方病平衡点E1存在,则E1为一个鞍点。 定理5假设地方病平衡点E2存在, a) 若有b[c(2αd+αr+αε+αk+λ)-β]≤2dac或 则E2是局部渐近稳定的。 b)若有 则E2是不稳定的。 记 4d2a2c2<2c(2αd+αr+αε+αk+λ)[βab2-4βa2b+βb2+2dacb-2ac2(2αd+αr+αε+λ)]+ββa2b2-4a3βc-b2β-4adcb。 证毕。 类似地,可以得到E3,E4的稳定性: 定理6若E3存在,则E3为一个鞍点。 定理7若E4存在, a) 若有b[c(2αd+αr+αε+λ)-m]≤2dac,或 则E4是局部渐近稳定的。 b) 若有 则E4是不稳定的。 定理8无病平衡点E0是全局渐近稳定的当且仅当下列两个条件之一成立: b) 由a)知当R0<1时,E1,E2不存在。若 此时P3 由此,在定理8的条件下,模型(1)不存在地方病平衡点。将模型(1)的两个方程相加有 则 解得 故模型(1)的一切正解是最终有界的,并且非负半S轴和非负半I轴均不是模型(1)的正解的正不变集。由定理3可知,当R0<1时,E0是局部渐近稳定的。根据Bendixson定理可知,当t→∞时,模型(1)的每个正解均趋向于E0。证毕。 以下利用Dulac函数来证明模型(1)的极限环的不存在性。由于Dulac函数是应用于光滑的向量场,所以当它应用于模型(1)时,应该注意由模型(1)所定义的向量场在I=I0上是不光滑的。 a)D是连续可微的, 则模型(1)不存在极限环。其中: 由引理9,可以得到: 定理10当λA<2d+ε+rd时,模型(1)不存在极限环。 当I>I0时, (12) 由于-rI-m<0,当λA<2d+ε+rd时,有 <0, 故可得:当λA<2d+ε+rd时,式(12)为负,从而可知模型(1)无极限环。证毕。 图1 后向分支数值模拟图 例2取a=1,b=1,c=1,d=1,α=0.01,ε=0.01,r=0.01,λ=0.01,β=0.01,I0=6,故通过计算可以得到b[c(2αd+αr+αε+αk+λ)-β]=0.032,2dac=2。从而可得b[c(2αd+αr+αε+αk+λ)-β]≤2dac,因此由定理5可知,模型(1)存在局部稳定的地方病平衡点E2,其稳定性数值模拟结果如图2所示。 图2 地方病平衡点E2的稳定性模拟结果 图3 地方病平衡点E3的不稳定性和E4的稳定性模拟结果 本文主要研究了一类带有饱和发生率和线性饱和治疗函数的SIS传染病模型。该模型中治疗函数采用线性饱和治疗函数,即:当治疗能力没有达到最大时,治疗率与感染者数量成正比;否则,采取最大治疗率。研究发现该模型至多存在4个平衡点,并利用定性分析的方法得到了各个平衡点的稳定性。数值结果验证了理论结果的正确性。当基本再生数小于1时,若饱和治疗率较小,常态预防能力过高或者采取最大治疗能力的时机过早,模型发生后向分支。故应选择适当的饱和治疗率、一定的常态预防能力以及选择合适的时机采取最大治疗能力,以避免后向分支的发生。

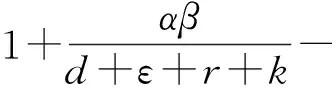
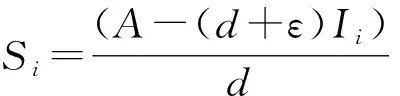


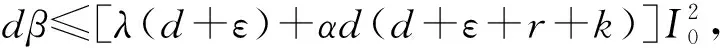
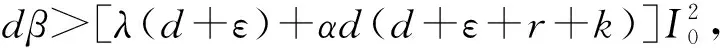
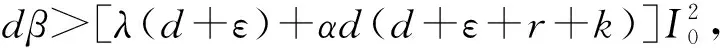

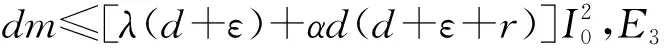


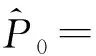

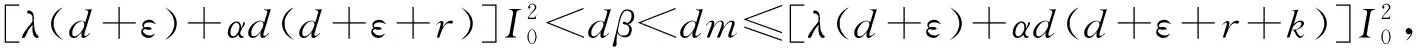
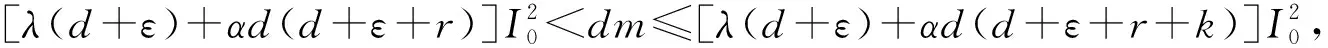

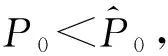
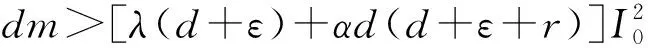
3 平衡点局部稳定性
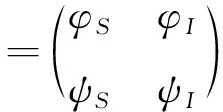

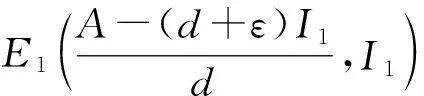

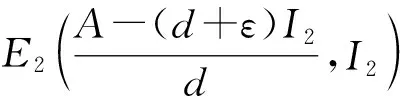
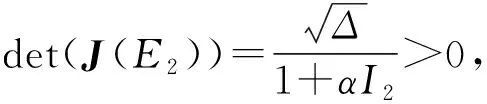
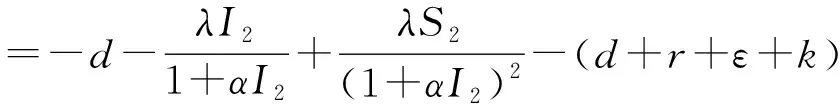

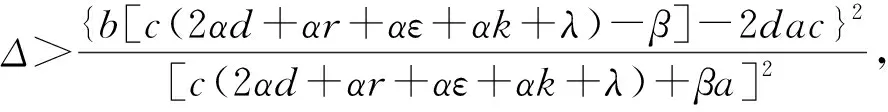
4 平衡点全局性质

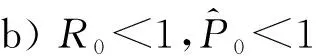
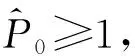



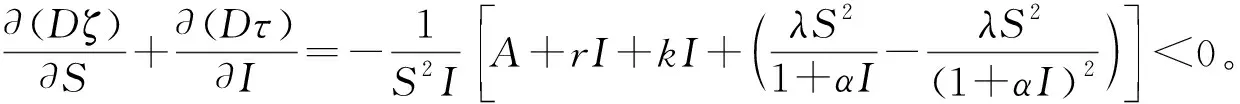
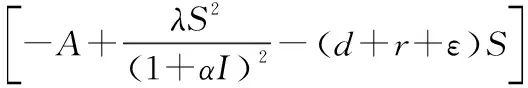
5 数值模拟
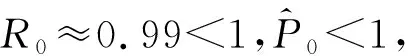

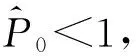

6 结 论

