2018年全国高考数学卷Ⅰ理科数学19题的多种解法与推广

安徽省灵璧中学 圣转红 (邮编：234200)

(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB.

所以AM的方程为

(2)解法一

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB；

当l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1,y1),B(x2,y2)，

从而kMA+kMB=0，故MA，MB的倾斜角互补，所以∠OMA=∠OMB.

解法二

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，设l的方程为x=my+1，A(x1,y1),B(x2,y2)，

故MA、MB的倾斜角互补，所以∠OMA=∠OMB.

解法三

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB；

当l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1,y1),B(x2,y2)，

过A、B分别作x轴的垂线，垂足依次为C、D，如右上图.∠OMA=∠OMB⟺

tan∠OMA=tan∠OMB

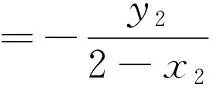
解法四

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB；

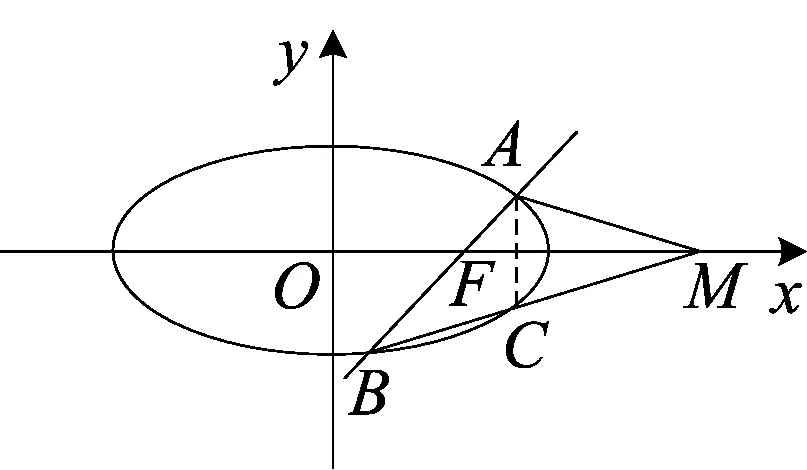
于是∠OMA=∠OMB⟺B、C、M三点共线

解法五

当l与x轴重合时，∠OMA=∠OMB=0°；

由角平分线性质知，∠OMA=∠OMB等价于点O到直线MA、MB的距离相等.

直线MA、MB的方程分别为(x1-2)y-y1x+2y1=0,(x2-2)y-y2x+2y2=0.

于是

以下同解法二.

解法六

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，设l的方程为x=my+1，A(x1,y1),B(x2,y2)，

则y1y2<0，x1=my1+1，x2=my2+1.

于是

因为y1y2<0，所以上式可整理得2my1y2-(y1+y2)=0.

因此∠OMA=∠OMB⟺2my1y2-(y1+y2)=0 .

以下同解法二.

解法七

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，设l的方程为x=my+1，A(x1,y1),B(x2,y2) .

以下同解法五.

解法八

当l与x轴重合时，∠OMA=∠OMB=0°；

由向量夹角公式知∠OMA=∠OMB

以下同解法五.

解法九

设直线l的参数方程为

则

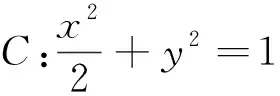
=0.

故MA、MB的倾斜角互补，所以∠OMA=∠OMB.

解法十

由条件可知，过M点垂直于x轴的直线x=2恰好是椭圆C相对于焦点F的准线.

当l与x轴重合时，∠OMA=∠OMB=0°；

当l与x轴不重合时，过A、B分别作准线的垂线，与准线依次交于C、D，如下图所示.

因此Rt△ACM～Rt△BDM，从而∠AMC=∠BMD，故∠OMA=∠OMB

推广

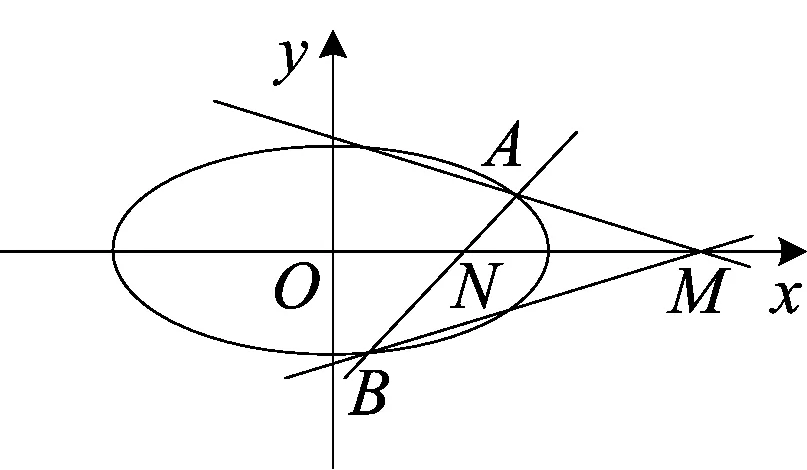
证明 当l与x轴重合时，直线MA和直线MB与x轴所成的角都是0°，此时mn可以取任意非零实数；

当l与x轴不重合时，设l的方程为x=ty+n，A(x1,y1),B(x2,y2) .则

得(b2t2+a2)y2+2tnb2y+b2(n2-a2)=0.

于是y1+y2=

因为直线MA和直线MB与x轴所成的角相等⟺kMA+kMB=0，

而kMA+kMB

综上，直线MA和直线MB与x轴所成的角相等的充要条件是mn=a2.

这个结论的证明只要将椭圆中的b2换成-b2即可，不再赘述.

结论三 已知抛物线C:y2=2pxp>0，M(m,0)、N(n,0)是x轴上不同的两点(异于抛物线的顶点).过点N作直线l与抛物线C交于A、B两点，则直线MA和直线MB与x轴所成的角相等的充要条件是m+n=0.

证明 由条件知直线l的斜率不为零，可设l的方程为x=ty+n，A(x1,y1),B(x2,y2)

则x1=ty1+n，x2=ty2+n，x1≠m，x2≠m.

所以y1+y2=2pt,y1y2=-2pn.

因为直线MA和直线MB与x轴所成的角相等⟺kMA+kMB=0.

于是2ty1y2+(n-m)(y1+y2)=2t·(-2pn)+(n-m)·2pt=-2pt(m+n).

又t∈R，所以kMA+kMB=0⟺-2pt(m+n)=0⟺m+n=0.

故直线MA和直线MB与x轴所成的角相等的充要条件是m+n=0.

特别的，当p=1,n=2,m=-2时，这就是2018年全国卷I文科数学20题：

设抛物线C:y2=2x，点A(2,0),B(-2,0)，过点A的直线l与C交于M、N两点．

(1)当l与x轴垂直时，求直线BM的方程；

(2)证明：∠ABM=∠ABN．

类似的高考题还有：

(1)当k=0时，分别求C在M点和N点处的切线方程；

(2)y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

(1)求椭圆E的方程；

2013陕西理20题：已知动圆过定点A(4,0)，且在y轴上截得弦MN的长为8.

(1)求动圆圆心的轨迹C的方程；

(2)已知点B(-1,0)，设不垂直于x轴的直线l与轨迹C交于不同的两点P、Q，若x轴是∠PBQ的角平分线，证明直线l过定点．