扎根教材 变式拓展 提高学考复习时效
——2018年4月浙江学考数学函数压轴题评卷感悟
浙江省海宁中学 李安毓 (邮编:314400)
摘 要 以2018年4月浙江省学考数学第25题函数压轴题为例,结合自己的阅卷经历与实践,谈谈个人的一些阅卷感悟,同时给出今后浙江省学考数学复习备考的一些建议,希望对一线教师同仁有所启示.
关键词 学考复习;评卷;感悟
2018年4月浙江省学考选考已落下帷幕,本次学考笔者有幸代表学校参加了省教育考试院组织的网上评卷工作.为期六天的数学学考阅卷工作,时间紧、责任大、任务重,虽然很累,但通过这项任务为下一届学考复习备考提供了真实素材,对今后进一步提高自身的课堂教学研究水平提供了有力保障.笔者本次参加的学考评卷题组是最后一道解答题第25题函数压轴题,该题全省平均分只有1.94分.作为解答题的压轴题,真正充分发挥了对不同层次的学生的区分功能,毕竟数学学考A等第的取得并非易事,能拿到A等第的也只是少数同学.就试题本身而言,有些学考试题如同高考试题一样往往起源于教材而高于教材,因此学考复习的有效性在于对教材的回归,作为一线教师要想提高学考复习实效,就应该引领学生从教材中来,回到教材中去.
1 考题呈现:似曾相识燕归来

图1
直线x=t(0 (Ⅰ) 分别求函数f(t)和g(t)的解析式; (Ⅱ)是否存在区间(a,b),使得函数f(t)和g(t)在该区间上均单调递减?若存在,求b-a的最大值;若不存在,说明理由. 作为本次数学学考卷的最后一题“函数压轴题”,该题主要考查学生分段函数及函数的单调性等概念,以及分段函数解析式的求解、函数单调递减区间的判断和证明等核心知识.本题以函数为载体考查学生运算求解和逻辑推理与证明等核心素养能力,以及“数形结合” 、“分类讨论”思想和分析问题、解决问题的能力.此题紧扣教材,作为数学解答题的压轴题,语言简练,无论是分段函数解析式的求解,还是函数单调性的讨论,都源于教材,解题时下手容易,但又层次多、区分度强,具有明显的“浙江特色”. 图1 图2 第(Ⅱ)问解法探究: 解法1 单调性定义的视角 从而 即 解法2 构造函数的视角 二次函数f(t)的单调性同解法1. 构造函数 从而 即 解法3 导数的视角 设 点评 该方法主要利用导数作为工具来研究函数的单调性,在学完导数知识之后证明或判断函数单调性有两种方法:一是单调性定义,一是利用导数工具来判断.相比之下单调性定义步骤比较繁琐,利用导数简单方便.但本题中由于函数g(t)解析式是一个分式函数形式较为复杂,求导计算量较大,很多同学求导出错,以至于判断单调性失败. 解法4 导数放缩的视角 二次函数f(t)的单调性判定同解法3. 解法5 二阶导数法的视角 查阅教材可以发现,在人教版必修1教材的复习参考题中找到了本道函数压轴题的源头. 图4 源头 (人教版必修1教科书第113页第三章《函数的应用》复习参考题B组第2题)如图4,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象. 点评 教材中的原型是求△OAB位于直线x=t(t>0)左侧的图形的面积表达式f(t)并画出图象,学考试题中命题者把它改为:求左侧部分多边形Ω各边长的平方和f(t)与倒数和g(t)的函数解析式,并探究f(t)和g(t)共同的单调递减区间.事实上,本道学考题就是对教材原题的一个变式拓展,设置梯度明显提升,尤其是第(Ⅱ)问设置了两个函数共同的单调递减区间的存在性问题,试题的探究意味浓厚并具有一定的开放性.很多一线教师往往更倾向于对高考题专门进行研究和赏析,殊不知有相当一部分学考题也是一道靓丽的风景线,是值得我们去开垦和挖掘的一块“宝藏”,就像这道来源于课本却高于课本的函数压轴题一样,从课本习题摇身一变成了一道精彩的学考试题.正如美国著名数学教育家波利亚认为:“好的问题如同蘑菇一样它们大都成堆生长,找到一个之后,你应当在周围再找一找很可能就有好多个”,在接近学生思维的最近发展区设置有探究价值的问题,变式拓展,鼓励学生积极参与探究,是提升学生数学能力素养的好途径! 本道学考函数压轴题全省平均分为1.94分,可见学生在这道函数题目上得分率非常低,在函数的复习中存在着很大问题,主要反映在以下方面: 教材中的例题和习题往往是学考题和高考题的一个发源地和素材聚集地,学考、高考试题源于教材却高于教材,近几年来无论是学考还是高考,命题人越来越重视对学生基本概念的准确理解和把握.因此在平时的学考复习中,应扎根教材立足基础,学考复习课应充分发挥教材中的例题习题以及探究题思考题的作用,接近学生思维的“最近发展区”合理地对教材中的典型题目进行变式提升、拓展推广,通过变式教学举一反三,抓住本质,深入挖掘其教学功能,从而使学生形成系统化、网络化的有机知识结构,才能跳出题海,提高学考复习时效.正如波利亚所说:“拿一个有意义又不复杂的题目去帮助学生发掘问题各方面,使得通过这道题就好像一道门户把学生引入一个完整的领域!” 在平时的学考复习教学中,除了对解题方法的训练,还应对学生的规范答题、优化答题做针对训练.例如在本道学考压轴题中相当一部分同学不知所云,写了一大片废话,逻辑混乱,丢分严重.阅卷给分的基本原则是踩点给分,而踩点给分的重点关注的是学生在解答过程中所呈现和暴露出来的思维过程,这就要求学生在解题时能够规范表达出思维过程.笔者认为,根本原因就是没有规范和优化答题意识,导致失分严重.教师在平时学考复习时,若能注重引导学生在解题步骤书写过程中,明确评分细则,分步书写循序渐进,教师应注重板书示范,让学生关注步骤的表述规范性和逻辑连贯性.同时学考毕竟是重要的考试,还应注意书写字迹清楚端正、过程整洁清晰,不随意涂改乱画. 现行的数学课堂教学中,很多名师和专家们都大力呼吁要关注和注重学生对“通性通法”的掌握,淡化特殊技巧避免巧解的机械训练.笔者认为,因为高考和学考试题的设置对 “通性通法”重点考查,我们的确应该加强通性通法的训练,但通性通法并不排斥巧法妙法的运用.作为一名明智的数学教师,我们不盲目追求“巧法妙法”的大量机械训练,但也应适当鼓励对某些典型习题的一题多解,用欣赏的眼光看待“巧解妙解”,提倡解法的多元化,多一种方法多一条出路.同时应注重因地制宜,因材施教,在基础薄弱的学校或班级重点关注学生对通性通法的掌握,在学生基础好、能力强、素养高的学校或班级在注重通性通法的基础上恰当渗透巧法妙法,使其在考场上走好寻常路,同时又要让一些具有创造性和发散性思维的学生能够脱颖而出!做好了这些,才有可能切实提高学考复习备考时效!2 解法探究:横看成岭侧成峰














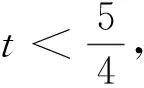
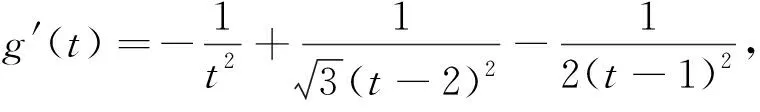
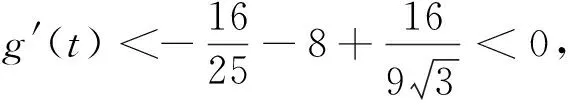

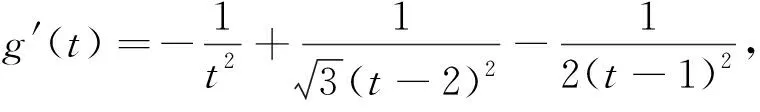



3 寻根探源:那人却在灯火阑珊处

4 学生答题情况综述

5 今后浙江学考数学复习备考建议
5.1 回归教材,关注基础,变式提升
5.2 注重答题规范性训练,提高学生的规范答题意识
5.3 立足通性通法,恰当渗透巧法妙法

