一道课本例题的推广与应用

安徽省宣城市第二中学 徐积松 (邮编：000000)安徽省亳州市涡阳县第一中学 葛蒙蒙 (邮编：000000)

北师大版教材必修5第48页，有这样一道其貌不扬的例题，很多老师在讲这一节课的时候，对这一例题都没有引起足够的重视.但是，这道小小的例题却蕴含着深邃的数学思想方法，在近几年的高考试题中大显身手.

1 教材例题呈现及简要证明

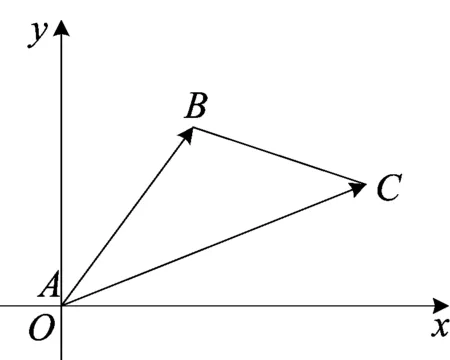
图1

所以

即△ABC在三个顶点坐标给定的情况下，可以先求出从某一顶点引出的两个向量的坐标，其交叉乘积之差的绝对值的一半，即为△ABC的面积.

2 应用教材例题的结果解高考题

用该结论解决2011年山东高考第22题，可以大大简化解题过程，比所给的参考答案要简单得多.

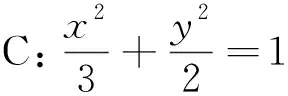
(II)设线段PQ的中点为M，求OM·PQ的最大值；

(III)略.

解 (I)依题可设

且0≤α<β≤2π.

由引理可知

所以

得sin(β-α)=1，

所以

当且仅当sin2α=0取等号.

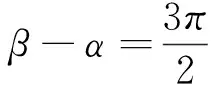
3 教材例题推广及简要证明

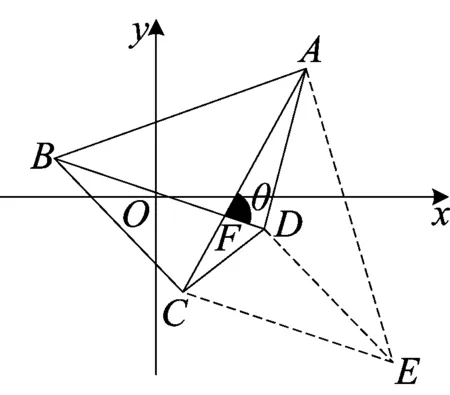
图2

该结论可推广到四边形.

如图2，凸四边形ABCD中，AC与BD的夹角为θ，设A(x1,y1)、

B(x2,y2)、C(x3,y3)、D(x4,y4)，

所以SABCD=S△ABC+S△ACD

如图2，过C作BD的平行线，截取CE，使CE=BD，连接AE,DE.

套用上述例题的结果，得

若直线AC,BD斜率均存在，不妨设斜率分别为k1、k2，对上式稍作变形得：

(*).

这个式子的特点是，只需四边形四点的横坐标，以及对角线所在直线的斜率，即可表示出面积，这一优点在圆锥曲线压轴题中异常好用，它将大大简化运算过程.

4 应用教材例题的的推论解高考题

利用这一结论，可以快速地处理2016年全国卷I理科数学第20题.

高考真题 (2016年全国卷I高考第20题)设圆x2+y2+2x-15=0的圆心为A，直线l过点B1,0且与x轴不重合，l交圆A于C、D两点，过B作AC的平行线交AD于点E.

(1)证明EA+EB为定值，并写出点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M、N两点，过B且与l垂直的直线与圆A交于P、Q两点，求四边形MPNQ面积的取值范围.

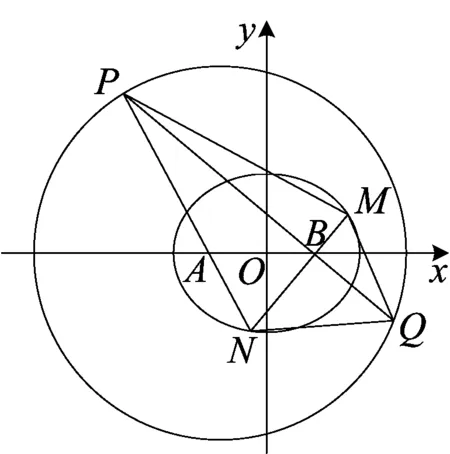
图3

解析 (1)略

(2)如图3，易知B(1,0)，当直线l的斜率存在时设其为k，则直线l:y=k(x-1)，

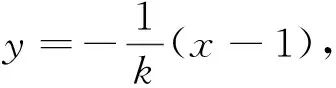
得(3+4k2)x2-8k2x+4k2-12=0，

得1+k2x2+2k2-1x+1-15k2=0，

则SMPNQ=

易得，当l与x轴垂直时，SMPNQ=12，

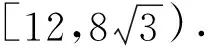
利用(*)式子还可以漂亮地处理这道高考题的变式，能起到意想不到的效果.

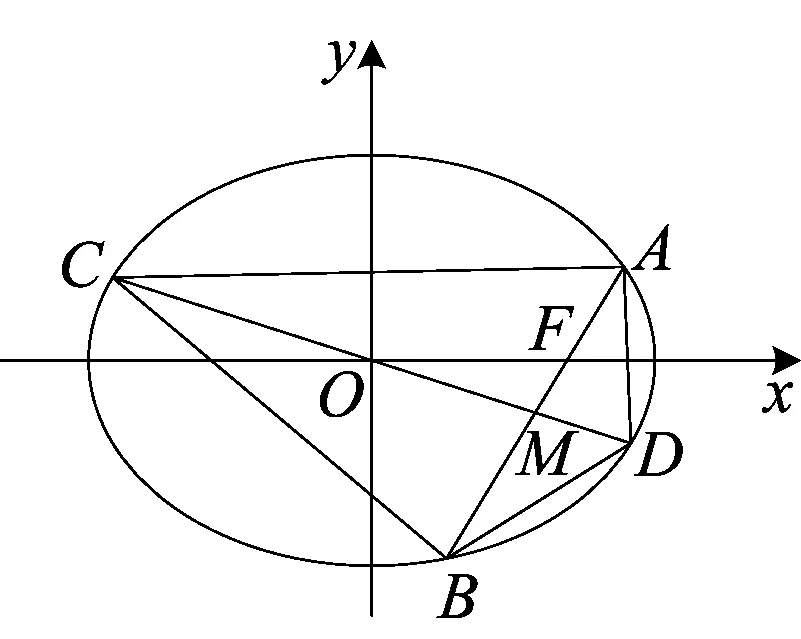
图4

分析 改变第二条直线的生成方式，此处由弦AB的中点M这一动点和原点构造出第二条直线，综合了中点弦的处理技巧.

解析 如图4，易知F(1,0)，则直线l:y=k(x-1)，

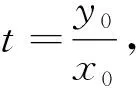
设A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)、M(x0,y0)，

不妨令x3<0，则x4>0，且x4=-x3.

(3+4k2)x2-8k2x+4k2-12=0，

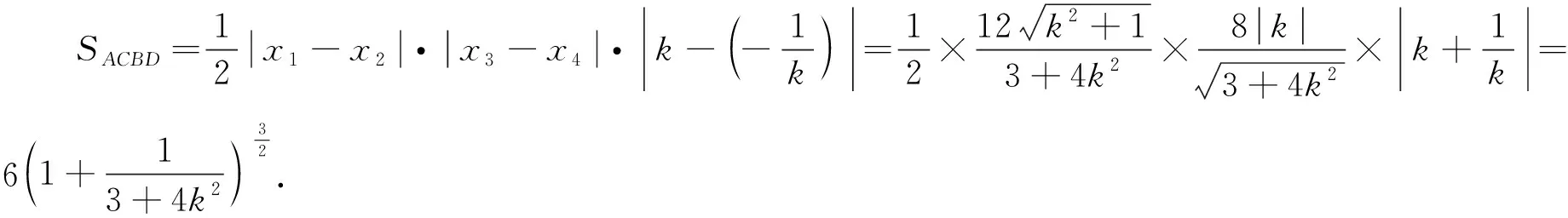
教材是我们学习的出发点和落脚点，应做到“入乎其内，出乎其外”，把教材由薄读到厚，再由厚读到薄.教材的每一段话、每一道例题、每一组习题，包括课后阅读材料、研究性学习，都要引起高度重视，只有这样，才能在高考考场上应对自如.