初三数学试卷讲评课的教学策略分析

王峰

[摘 要] 本文从初三数学的教学实践出发，探讨了提升数学试卷讲评效率的基本策略，指出教师要充分运用大数据来对试卷进行统计分析，同时还强调教师在试卷讲评的过程中要善于借题发挥和有效拓展.

[关键词] 初三数学；试卷讲评；策略分析

试卷讲评课一直是初中数学最重要的教学环节之一，它具有纠正、示范、激励等作用. 到了初三，学生的训练更加频繁，试卷讲评课也比较多，同时初三数学的教学时间非常紧张，于是如何在有限的时间内将试卷讲评工作效率提升起来，便需要教师在教学中进行深度分析和探索. 下面，笔者介绍一些自己的做法和体会.

试卷讲评需要教师积极进行统计分析

要让试卷讲评更有效率，我们必须对批改过的试卷进行统计分析. 以往的手工操作往往是逐张试卷批阅，并且以画“正”字的方式进行，这种做法如果放在初一或初二，可能还有较强的操作性，但如果放在初三，则操作性不强，因为教师没有那么多精力来完成这些操作.

幸运的是，当前的大数据系统能够帮助我们做好这些统计工作. 下面以智学网系统为例. 学生作答的试卷经过扫描后，可以在网上进行阅卷，阅卷完成后，它不但能智能化地汇总成绩，还能对各个问题的得分情况进行统计分析，且直接提供汇总数据. 由于很多工作都是电脑完成的，因此某些数据的统计相当细致，图1即为某次考试一道选择题的学生解答情况统计，可以看到，学生解答本题时，选择正确答案的人数为25，占比69.4%，选择错误选项的学生也能通过数据看出具体分布. 此外，如果点击柱状图，还可以看到对应学生的名单，这样将方便我们讲评试卷时对部分学生进行针对性引导.

在进行考试数据分析时，我们不但要看到学生的试卷作答情况，还要结合试卷命制时的双向细目表来研究学生的学习状况，这样才能让考试的诊断作用充分发挥出来. 当然，这也有利于我们讲评试卷时更有侧重点.

试卷讲评需要教师善于解题发挥

经常听到很多同事这样抱怨：“为什么无论讲什么问题，只要我们变一个数据，学生就会做错呢？”其原因在于，教师在处理试卷时仅仅是孤立地就题论题，以至于学生只是在这个题目上知道了答案而已. 事实上，数学试卷的讲评绝不能只是答案的核对，教师要善于解题发挥，从而起到“以点带面”的教学效果.

1. 采用一题多解的问题讲解方法

很多数学问题，如果用不同的方法思考，就可以获得不同的问题解决思路，这样的处理不但能拓展学生的思维，还能优化学生的问题分析方法. 在讲评过程中，教师不能有太多的铺垫，我们要直接将问题展示出来，且引导学生将最原始的思维暴露出来. 同时，我们还要鼓励学生打破传统的常规思维，以一题多解的方式让学生体验到殊途同归的数学美感. 当然，一题多解也并非方法越多越好，教师要引导学生对分析方法进行比较和筛选，这样才能让学生的思维得到真正的优化.

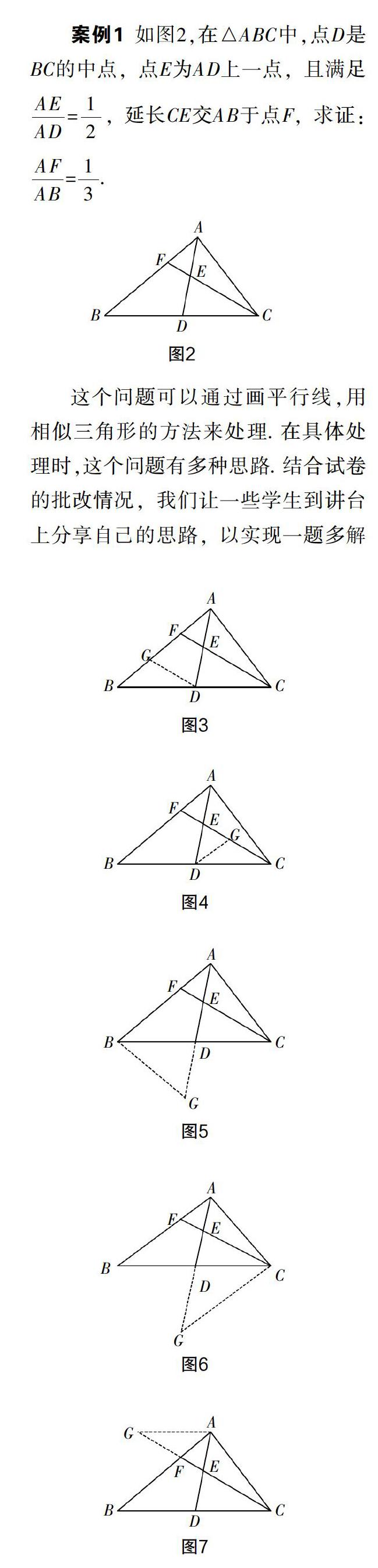
案例1 如图2，在△ABC中，点D是BC的中点，点E为AD上一点，延长CE交AB于点F.

这个问题可以通过画平行线，用相似三角形的方法来处理. 在具体处理时，这个问题有多种思路. 结合试卷的批改情况，我们让一些学生到讲台上分享自己的思路，以实现一题多解的效果：有的学生是过点D作CF的平行线交AB于点G，如图3；有的学生是过点D作AB的平行线交CF于点G，如图4；有的学生是过点B作CF的平行线交AD的延长线于点G，如图5；有的学生是过点C作AB的平行线交AD的延长线于点G，如图6；有的学生是过点A作BC的平行线交CF的延长线于点G，如圖7.

学生进行讲解时，教师不仅要关注他们思路的正确性，还要关心他们描述的科学性，同时引领他们对不同解决思路进行比较，由此引导学生在对比中总结出此类问题的常规解法. 这样的处理方式，有助于提升学生思维的灵活性，也将直接提升学生的解题效率.

2. 采用一题多用的问题讲解方法

如果我们将一题多解视为一种拓宽学生思路、训练学生思维变通性的重要手段，那么一题多用则有助于学生更加系统地认识数学知识，继而提升他们的归纳能力和应用意识. 须知，数学试卷讲评过程绝不是一个纠正错误的过程，我们要帮助学生在此过程中完成对思维的提炼. 教师在讲评试卷时，应尽量帮助学生实现对问题的反思，推动“读薄”书本过程的发展.

案例2 现有一条直线l，其上有n个点，则该直线上一共有多少条线段？

这个问题比较简单，答案为，如果讲解时，我们仅局限于告知学生答案，那这个问题的讲解便没有多少价值. 为了提升讲解质量，笔者借助这个问题，提取出模型，引导学生处理了很多数学问题，如

（1）在育才中学97届的校友回校聚会中，学生和老师共37人，如果每两个人要握一次手，那么这次聚会共握手多少次？

（2）已知A，B两个城市之间的铁路沿线共有15个停靠站，如果每两个停靠站点之间需要安排一种车票，则需要设计多少种不同的车票？

（3）三号车间共有工人10人，现要选举2人作为代表参加第二天的慰问大会，李华和张强同时被选中的概率有多大？

以上问题可以通过同一个模型来分析、解决，因此将此类问题放在学生面前，让他们在比较中思考和讨论，不但能提升他们的归纳整理能力，还能提升他们的建模水平和应用模型意识.

试卷讲评时教师要注意进行拓展

在试卷讲评的过程中，教师要仔细分析试卷所涉及的知识点和相关技能，要针对学生考试过程中所出现的问题展开分析和探索，并及时进行补救. 同时，我们还要将原有问题进行适当包装、处理，以改头换面的方式呈现在学生面前，从而改变以往就题论题的单一讲解模式，让学生的应变能力在试卷讲评过程中得到提升.

案例3 如图8，△ABC内接于⊙O，AB是⊙O的直径，∠A=30°，BC=3，求⊙O的半径.

学生在这类问题上的得分率较高，如果我们的讲解仅仅局限于这个问题，学生便很难提起听讲的兴趣. 为此，我们要对问题进行拓展处理，基本操作如下：

（1）如图9，在其他条件不变的情形下，如果AB不是⊙O的直径，则⊙O的半径如何？

面对这样一个问题，学生可能会认为此题不能再用直角三角形的方法来处理了，但这其实是定式思维的作用，对此，教师应适当引导，启发学生将现有问题转化为原有问题进行分析，最终完成问题的解决.

（2）若∠A=α，BC=a，答案又如何？

学生借助之前问题的处理方式进行更进一步的思考，很快便完成了此题的解答. 但问题的处理并不能就此结束，我们还要继续引导学生展开反思与总结：①结合上述对问题的分析和探讨，你在此类问题的解决方法上有什么收获？②在这些问题的处理过程中，你有什么发现和体会？通过这一系列问题的讨论，我们将引领学生重新感悟知识和方法的形成与发展过程，学生也将从中形成更加深刻的认识和理解.

综上所述，高效的试卷讲评应该是一个有针对性、有发挥、有拓展的教学过程，我们希望学生能够在试卷讲评过程中对数学知识进行更系统化的梳理，以更加灵活的思维来认识和研究数学问题，这样才有助于学生理解与掌握数学方法和有关思想.