加劲环钢管均匀外压弹性屈曲解的对比分析

齐文彪，张 明，郑双凌，李国栋，3，马吉明

（1.吉林省水利水电勘测设计研究院，吉林 长春 130021；2.清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084；3.内蒙古大学 交通学院，内蒙古 呼和浩特 010070）

1 研究背景

露天或埋藏式的压力钢管广泛应用于水利水电等工程中［1-4］，其管壁都很薄，尤其是高强钢钢管，太厚则卷板容易造成塑性变形进入强化阶段，塑性损失大，若因厚板焊接的焊接残余应力较大，还要进行消除应力的热处理。在停机、检修的放空工况下，受管外大气压力或外水压力作用下，钢管的稳定性成为重点考虑的问题。对钢管进行环向加强可能比单纯增加管厚更有效，也更节约钢材。

压力钢管外压屈曲的环向预防措施通常采用加劲环。加劲环是管道上沿圆周方向设置的局部加劲部件，可用钢板、角钢、T形钢或槽钢等沿管环向焊接而成。与无加劲环的光面管道相比，带加劲环的薄钢管的外压屈曲具有不同的特点［5］。加劲环的存在使管壁的屈曲变形受到阻碍，波数增多，波幅减小，单凭直觉确定加劲环管的屈曲变形是比较困难的。

加劲环间管道可模型化为两端受约束的圆柱壳［6］。研究两端受约束的圆柱薄壳的外压屈曲在管道、压力容器等设计中也尤为重要。在进行理论分析时，加劲环通常被假定为对环平面外没有刚性，只对环平面内的变形有刚性。加劲环对管道全部作用可以通过数值仿真或试验来揭示。

理论研究［6-8］表明，加劲环的间距对增强效果影响显著，当加劲环相距很远，加劲环对较远处的管壁不施加显著影响，此时加劲环管与光面管具有相近的屈曲压力。两端受约束的圆柱薄壳有一个临界长度［7，9-11］，再长就跟无限长圆柱薄壳的屈曲问题一样了，因此加劲环管也具有一个可忽略加劲环的最小环间距值，可称为临界间距。水电站压力钢管外压稳定设计的基础依然是这些理论分析成果。数值方法［12-14］或试验方法［9，15-18］能考虑更为复杂的加劲环管道的外压屈曲问题，如可考虑管道的初始缺陷、管道与加劲环的相互作用和管壁与管外混凝土间的初始缝隙等，则更接近实际情况。

均匀外压作用下加劲环管的屈曲临界压力的精确解析表达式比较复杂，出于不同的考虑对其简化是必要的，我国水电站加劲环钢管设计就是利用了简化后的表达式。弄清简化式与精确解的差别，对设计规范的安全裕度做到心中有数也是必要的，而且辅以计算机更为复杂些的设计表达式已不再是一个问题。此外，利用有限元精细计算，考察这些精确的或近似的解析解与实际加劲环钢管的屈曲临界压力的差别，能更准确地确定加劲环管的设计安全系数。

2 均匀外压作用下加劲环钢管的屈曲分析

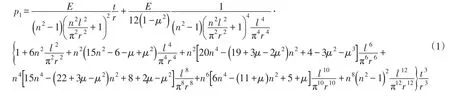
2.1 临界外压的解析计算一段圆柱薄壳（例如半径r与壁厚t之比r/t＞10）受均匀径向外压作用，其两端面简支，端部径向变形受到约束从而保持端部的初始圆形，端部的轴向变形和转角不受限制，则关于该段圆柱壳的弹性屈曲外压，有以下著名的Mises解［6］：式中：E、μ分别为圆柱壳的弹性模量和Poisson比；l为圆柱壳的长度；n为圆柱壳屈曲时在整个圆周条带里的波数。根据式（1），上述圆柱壳在外压下的稳定取决于材料物理力学性质，也决定于其长径比和厚径比，屈曲外压与弹性模量的单位相同。将薄壁圆管的加劲环理想化为上述简支座，即认为理想化的加劲环只约束加劲环处的径向变形保持该处为初始圆形，不限制管壁的倾斜，则式（1）就是加劲环间管的弹性屈曲外压公式。

式（1）是理论上的精确解，为了更便于应用，可对其进行简化。例如，一个被我国设计规范［1］所采用的近似表达式为：

又如，文献［10］给出、被文献［19］采用的近似表达式为：

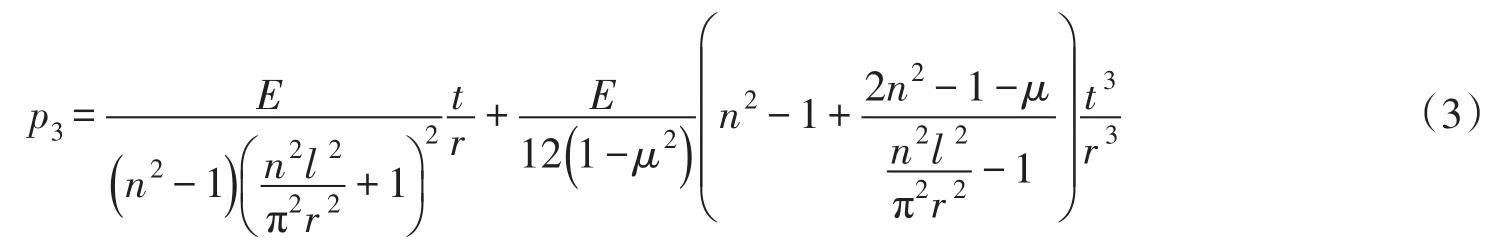
式（1）可写成［10］

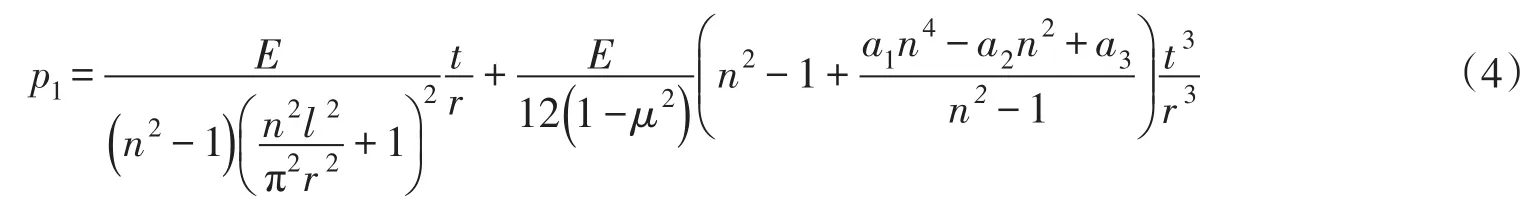
其中：a1=b（2-b）/（1-b）2，a2=（3+μ）b+（1-μ2）b2，a3=（1+μ）b-（1+μ+μ2）b2-（1+μ）（1+μ2）b3+μ（1+μ）2b4，b=1/［n2l2/（π2r2）+1］。

式（2）是在式（4）中令a1=2b，a2=（3+μ）b，a3=（1+μ）b，即忽略含有b的1次以上的项而得到的。式（3）也出于同样考虑，但略微减小了第2项中的分母。式（4）看似简单，但参数a1、a2和a3意义不明确，和式（4）同时都含有变量n和l/r。

可以设想，加劲环相距过远，不能有效约束管的屈曲变形，屈曲波形与光面管的接近，有2个屈曲波。特别地，当环间距l→∞时，n=2，则式（1）—式（3）均可化为光面管的屈曲临界外压公式，即［1，11］：

加劲环管的弹性屈曲临界外压即由式（1）、式（2）或式（3）给出的pi（i=1，2，3）的最小值。在管的材料和几何参数给定后，pi仅是波数n的函数。此时临界外压的求解就成为了一个非线性整数规划问题，即：

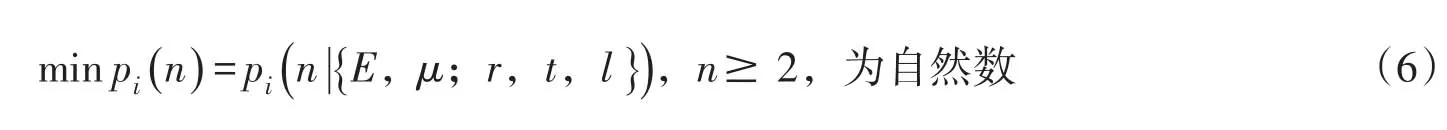
可先解与此整数规划问题对应的松弛问题，将所得到的n化为最接近的自然数，再求出与此自然数对应的外压值。通常可枚举试算或利用在一定实用区间的表达式或图表［1］。

2.2 屈曲外压公式的差别分析式（2）减去式（1），可得：

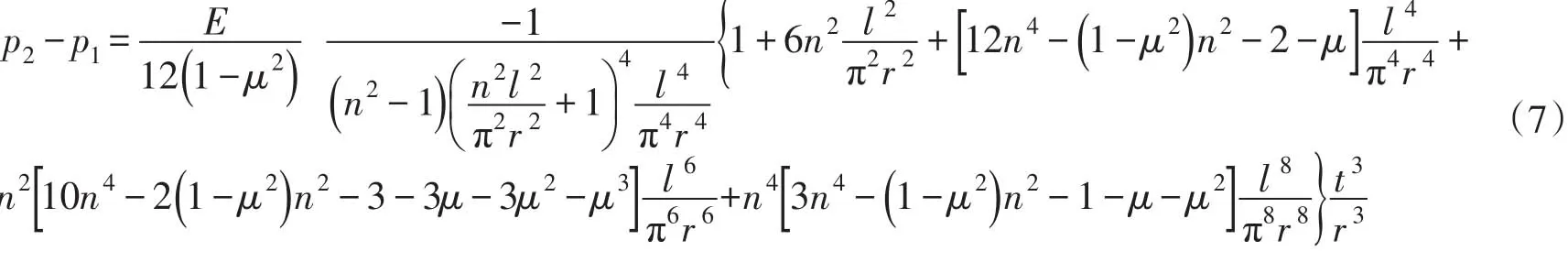
注意到0＜μ＜0.5，n≥2，容易验证式（7）的大括号中关于l/（πr）的多项式的系数均为正，于是可知p2＜p1。

式（3）与式（1）之差为：

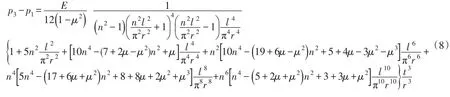
在式（8）中，同理容易验证大括号中关于l/（πr）的多项式的系数均为正，但是因子n2l2/（π2r2）-1的符号取决于环间距l。当l＞ πr/n时，p3＞p1。当l＜ πr/n时，p3＜p1。

式（3）与（2）式相减，得：

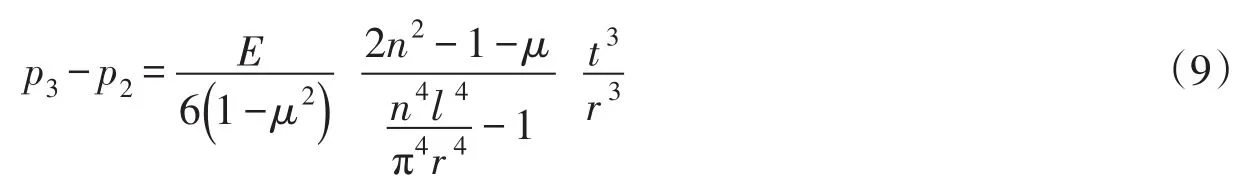
显然，l＞ πr/n时，p2＜p3；l＜ πr/n时，p2＞p3。

当波数n增多时，式（7）和式（8）均表明，近似的式（2）和式（3）与精确式（1）的差别会缩小，而根据式（9），式（2）和式（3）的差别也会缩小。

近似式（2）总是无条件地比精确解式（1）小，在设计上更为保守，形式也比较简洁，因此被我国规范采用，以下主要针对式（1）和式（2）进行分析。在通常的环间距情况下，式（3）比式（1）大，当然也比式（2）大。只有在管道上的加劲环很密集的情况下，式（3）会比式（2）还要小，自然也比式（1）小。

长期以来，加劲环式钢管屈曲外压不同计算公式的上述差别被忽略，分析它们的差别有一定的意义，例如工程设计中可采用式（2），不宜采用式（3），但作为有限元等数值方法的检验［12］则是不妥的，应当利用式（1）。

近似解的精度分析，如式（2）和式（3）哪一个更接近精确解（1），从式（7）和式（8）知是十分困难的，可以通过有限元法结果加以验证。

2.3 加劲环临界间距的确定当加劲环的间距大到一定程度，对管的外压屈曲的影响变弱，加劲环管的屈曲变形与光面管的接近，用式（1）—式（3）得到的屈曲临界外压与式（5）算出的区别很小，这样的间距可认为是加劲环的临界间距。在临界间距范围内，需要考虑加劲环对管的外压稳定性的增强作用，否则可按光面管处理，由此造成的误差可忽略不计。

加劲环的临界间距l0的取值并无定论。Southwell［7］根据很不准确的屈曲外压公式的分析并取Pois⁃son比μ=0.3后得到l0/r=3.85（r/t）1/2，而l0/r=4.90（r/t）1/2是Cook［9］的试验结论并被文献［11］采用。

加劲环的临界长度不仅取决于管径和管厚，应当还和忽视加劲环而采用光面管临界外压公式的容许误差有关。参照文献［7，9］，设加劲环的临界间距相对值为：

这样只需确定乘子k即可。

用式（10）的l0替代式（1）中的l计算p1，此即意味着管的屈曲波数n=2。假设p1与式（5）所得p0（＜p1）的相对误差为5%，即（p1-p0）/p0=0.05，此式与弹性模量E无关，仅与Poisson比μ有关，可令μ=0.3。经过化简整理，可得到确定k的方程为：

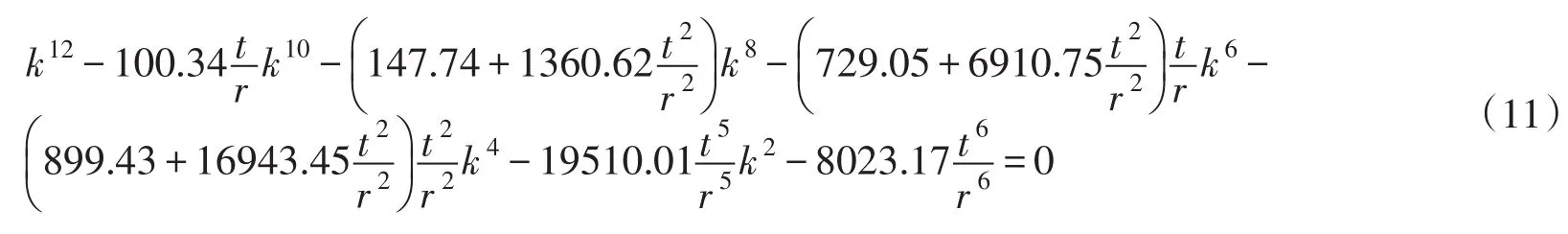
给定t/r，由多项式方程（11）可解得12个根，仅取其中唯一的正实数根。从式（11）可发现，当t/r→0时，方程趋于k4-147.74=0，亦即对于t/r很小的钢管，k十分接近于3.4864。式（11）在一些薄壁管t/r下的k值列于表1，此t/r范围已能包括水电站压力钢管的厚径比［20］。

表1的结果可拟合成下式：

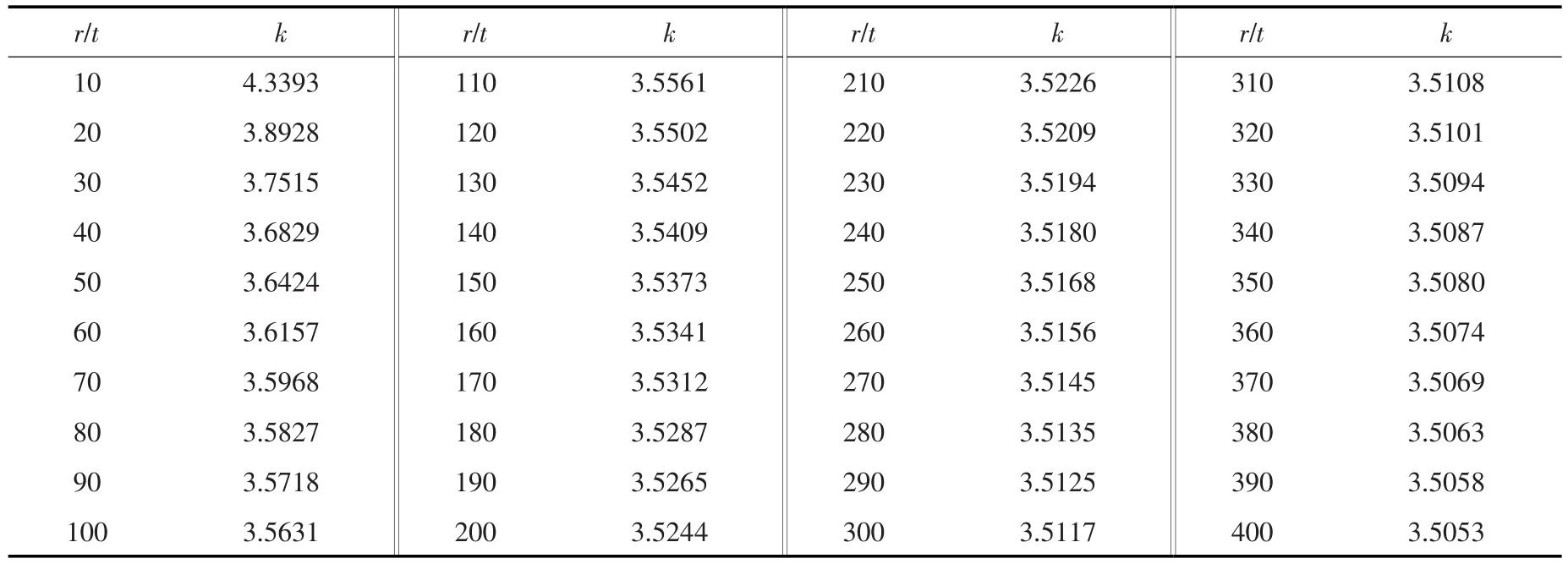
表1 式（11）的解k

与得到式（11）同理，令n=2，μ=0.3，将式（2）的l换以式（10）的l0，按所得p2和式（5）所得p0相差不超过0.05p0的原则，可得以下确定k的方程：

式（13）在水电站工程常见的r/t下的解列于表2，式（14）是对表中数据的拟合。

表1和表2的数据点，以及式（12）和式（14）给出的曲线，都描绘在图1中。从图1看到，精确式（1）和近似式（2）所确定的加劲环临界间距，其数据点相差甚微，曲线异常接近，说明两式所对应的加劲环临界间距差别很小，可以统一给出。

经过对数字的圆整化，本文建议加劲环临界间距式（10）中的k按下式确定：

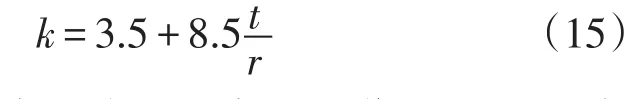
式（15）的曲线也表示在图1中，它位于上述所有数据点和曲线的上部，在5%容差的基础上又保守了一些。利用式（15）来确定临界间距，比前述k=3.85［7］或4.90［9］一刀切的办法，进一步计及厚径比的影响，又趋合理，所采用的方法和原则对其他材料（Poisson比不同于0.3）的管道也是适用的。

加劲环的临界间距不同于加劲环的等效翼缘宽度［20］，通常较大。例如，如果管的r/t=100，即便按照式（15）和式（10），临界间距l0也可达35.85r，远比加劲环的实际设置间距［20］大。由此看来，在实际水电站工程中，压力钢管的加劲环对其外压稳定均有帮助，优化加劲环的间距必要的。

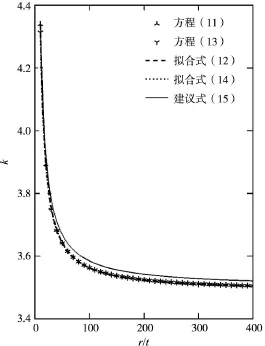
图1 加劲环临界间距l0=kr（r/t）1/2的乘子k

3 均匀外压作用下加劲环钢管的屈曲分析精度

3.1 解析计算公式的精度分析设一段钢管半径r=1.5 m，壁厚t=1 cm，两端设置加劲环，间距为l=1.5 m。钢材的弹性模量E=206 GPa，Poisson比μ=0.3。容易验证，加劲环间距小于式（15）给出的临界间距65 m，因此有必要考虑加劲环的影响。

对此钢管，利用式（1）、式（2）或式（3）即可算出不同屈曲波数所对应的屈曲外压，或者直接求解相应的非线性整数规划问题（式（6）），可直接得到弹性失稳时的临界外压及其屈曲波数。而用有限元法做特征值屈曲分析，可获得各阶屈曲外压，还能够直观显示相应的屈曲模态。

计算采用有限元软件Abaqus。在特征值屈曲计算中，边界条件是相对于屈曲过程中的增量位移，而不是屈曲前由作用力引起的总位移而定义的。因此，边界条件可以为：管两端的径向位移为零，中段的圆周上轴向位移为零。采用4节点曲壳单元S4R，这种单元可用于薄壳或厚壳结构建模，采用减缩积分方式，包含沙漏模式控制，容许有限薄膜应变。划分单元时最大尺寸为0.02 m，共划分 个单元。网格剖分很密，是为了保证有限元计算结果较为可信，可与解析计算相互参照。

钢管的第1阶屈曲模态见图2，为轴向半个波、周向9个波。图2（c）还显示，管端不再位于一个平面内，出现了交错鼓起翘曲。前9阶屈曲外压和波数列于表3，相应的解析计算值也同时列出。图3为根据表3数据所绘局部放大图，描绘了屈曲外压随屈曲波数的变化。

图2 加劲环钢管的屈曲模态

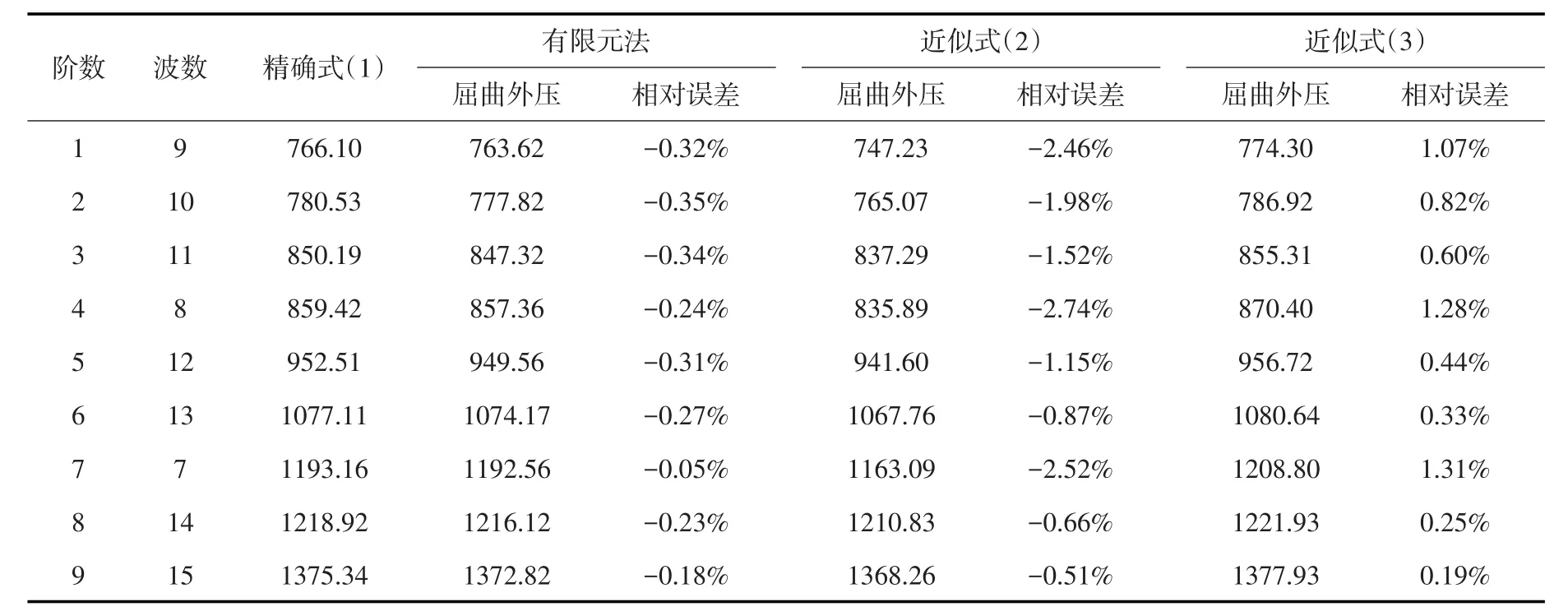
表3 加劲环钢管的屈曲外压 （单位：kPa）

表3和图3表明，有限元解与精确式（1）的解最为接近，说明本文改写成的表达式正确无误；式（3）比式（2）更接近于精确解，而且屈曲波数越大，其差别越小，也越准确。通过比较再次验证了通常情况下，精确解式（1）大于近似解式（2）、小于近似解式（3）。

考虑增大加劲环间距，l=3 m，其他条件均不变。按同样的单元划分标准，共划分 个S4R单元。表4给出前9阶屈曲的计算结果以及相应的解析解。近似解与精确解的大小关系以及接近程度等的规律依然与前相同，不同的是因为环间距的增大，屈曲压力显著降低，而且在第9阶屈曲时，当外压为870.15 kPa时的屈曲模态不再是沿轴向半个波，而是1个完整的波，管中段圆周成为2个半波间的节圆（见图4），此时解析解已不再适用。

3.2 实际加劲环钢管的解析解与有限元解的比较实际的加劲环除具有较大径向刚度以实现抵抗径向变形的功能外，在管轴方向也有一定的抗弯刚度，而且由于管道较长，加劲环自身沿管道轴向的变形为零或几乎为零。这样，水电站等工程中的管道，在加劲环等处的位移和转角都会受到某种阻碍，与加劲环仅限制管的径向位移的标准情况不完全一致，其弹性屈曲很难完全用解析方法分析。

以下考虑3种依次加强的加劲环约束：（1）约束A，一端约束径向位移，另一端约束径向位移和轴向位移；（2）约束B，两端均约束径向位移和轴向位移；（3）约束C，两端均施加固端约束，限制所有位移和转角。水电站中，靠近伸缩节处的加劲环约束比较接近于约束A，镇墩与厂房混凝土墙对钢管的约束比较接近于约束C，长钢管上的加劲环在管道屈曲时不会沿轴向移动，适合用约束B模拟。

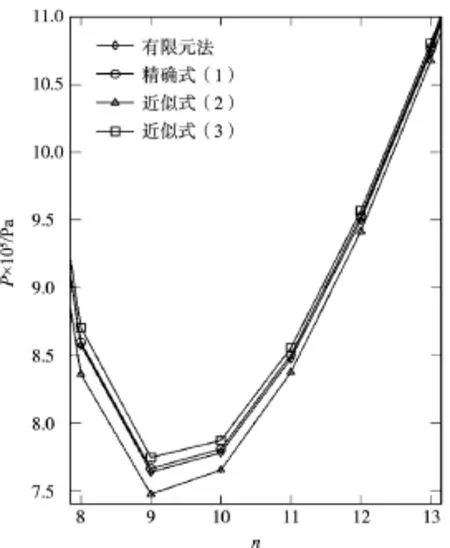
图3 不同屈曲波数对应的加劲环钢管的屈曲外压

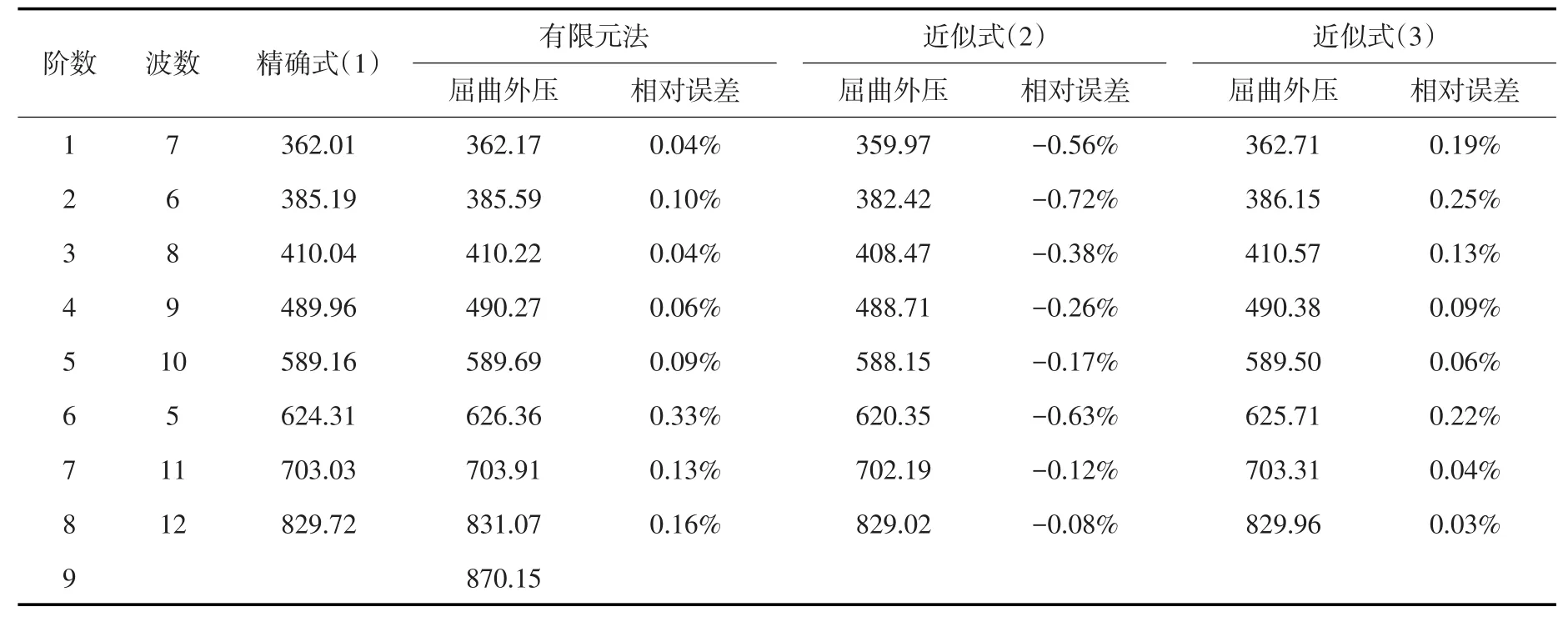
表4 加劲环间距增大后钢管的屈曲外压 （单位：kPa）

图4 加劲环钢管的具有2个轴向半波的屈曲模态

以前述钢管为例，加劲环间距l=1.5 m，利用有限元法计算在3种加劲环约束下的屈曲外压，并与理论解作对比。理论解可通过式（1）相应的非线性整数规划问题解得。

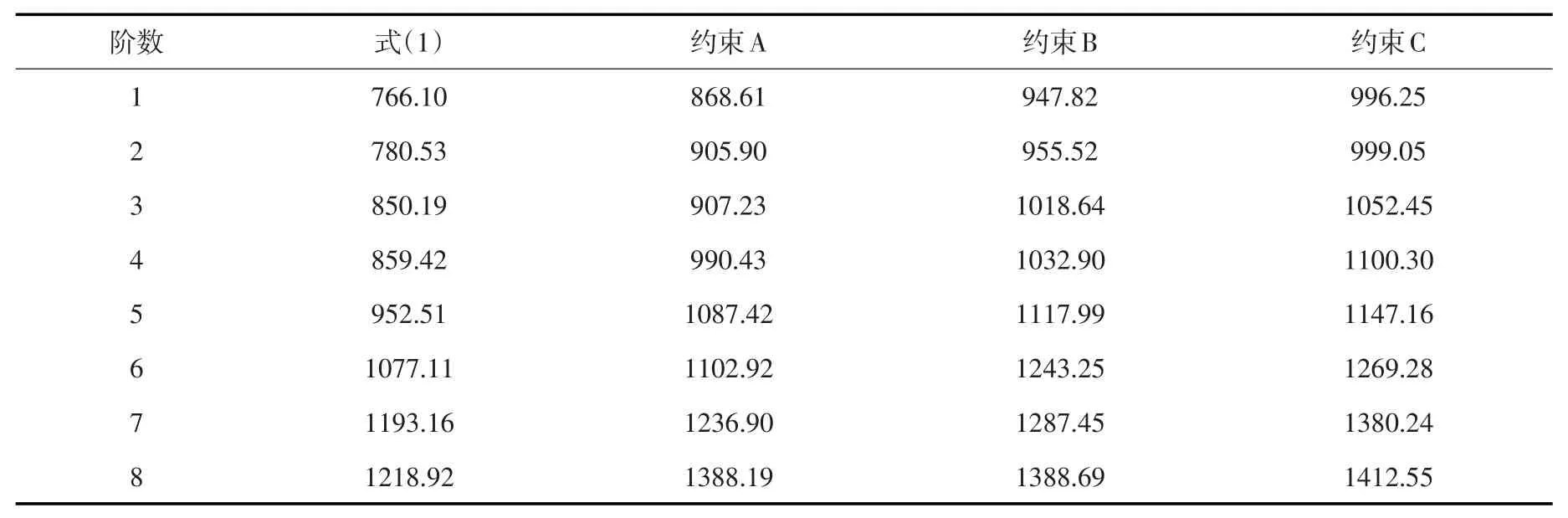
表5 钢管在加劲环不同约束下的屈曲外压 （单位：kPa）

表5给出了钢管在不同加劲环约束下的前8阶屈曲外压。从表5可见，加劲环约束的增强提高了钢管各阶的屈曲外压包括临界屈曲外压，约束越强则屈曲外压越高。

表6给出了不同环间距的钢管在不同约束下的临界外压及其提高程度，其中包括水电站常见的加劲环间距如l/r=0.5～5.0。由表6可知，实际水电站压力钢管的临界外压，比按式（1）的估计值高出不少。例如，按最为常见的约束B、l/r为1～2考虑，可比按式（1）的设计高20%～30%，加劲环较密时提高率相对较低，加劲环较疏时提高率还要更高。钢管端面在约束B或约束C下始终处在同一平面，文献［13］的有翘曲是不符合实际的。

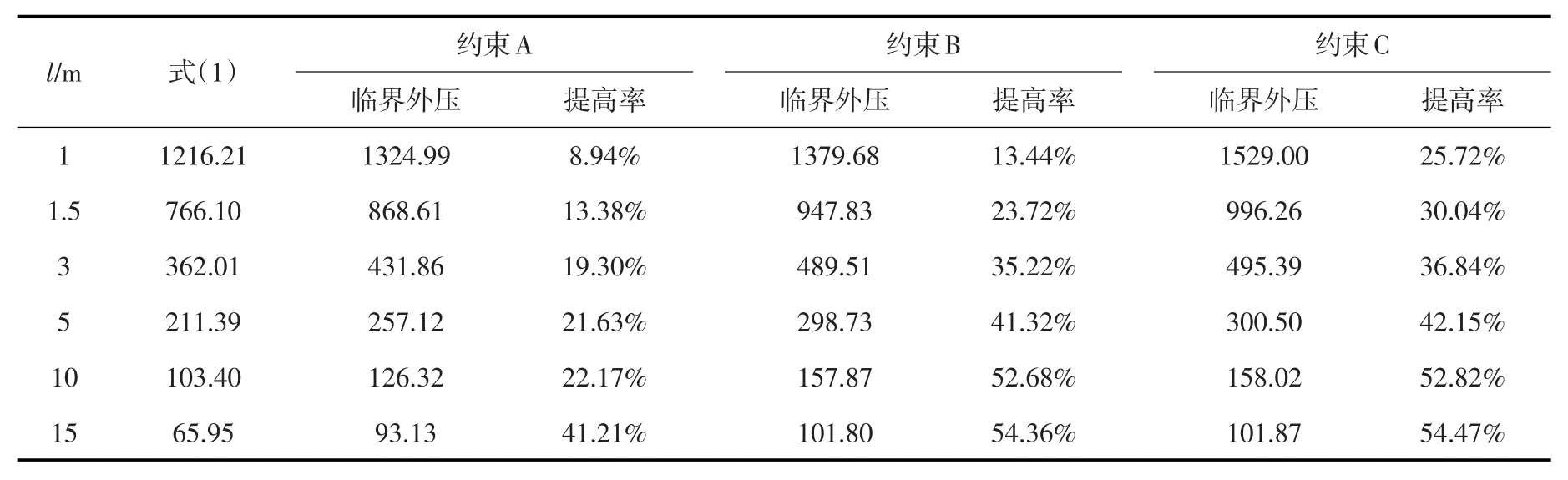
表6 钢管在不同间距的加劲环约束下的屈曲临界外压 （单位：kPa）

任何超过标准约束的加固都提供了额外的安全度。因此，就水电站的实际情况而言，精确式（1）已经是偏于安全的，规范采用的式（2）就更加保守了。

4 结论

本文分析了加劲环管均匀外压弹性屈曲压力公式，对其精确式与简化式做了比较，推导了加劲环的临界间距，考察了临界压力解析解与有限元解的偏差。主要结论有：（1）加劲环管均匀外压弹性屈曲压力公式是临界压力解析求解的基础，决定了临界压力值的精确程度，其简化式给出临界外压的近似解。我国水电站加劲环压力钢管设计采用的简化式给出的临界外压小于精确解，这是在设计中需要明确的。（2）屈曲外压公式仅考虑加劲环的径向约束作用，与加劲环管的工程实际不完全相符，给出的屈曲临界外压均偏小，完全依靠解析解进行设计是保守的，我国水电站加劲环钢管设计则更加保守，这也是需要明确的。加劲环管的外压稳定性分析和设计可辅以有限元法等更接近实际的方法，以考虑实际加劲环的嵌固作用。（3）当加劲环的间距过大以至超过临界间距时，加劲环管可按光面管分析其外压稳定性。临界间距应综合考虑管道厚径比的影响，按式（10）和式（15）估计是比较合理和稳妥的。水利水电等工程中管道上的加劲环间距均较密，小于临界间距，加劲环对管的外压稳定性的作用都很显著，不能忽略。