基于Richards方程切换的土壤水流及溶质运移数值模拟

曾季才，查元源，杨金忠

（武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

1 研究背景

土壤饱和-非饱和带是农业、生态、水文地质及陆面水文过程中的重要环节，研究饱和-非饱和土壤水分运动规律，对地下水资源管理、土壤水环境演变，及水文循环系统具有重要的科学意义。1930年代以来，基于质量守恒及达西定律的Richards方程［1］被广泛用于饱和-非饱和带水分运动数值模拟［2］。原始的Richards方程以含水量θ为水量衡量变量，以压力水头h为势能驱动变量，因而往往被称为混合型Richards方程。为求解这种带有两个未知变量的二阶偏微分方程，需要借助土壤水分特征曲线［3］来消除其中一个变量，因而得到分别含水量（θ）和压力水头（h）两种形式的Richards方程。Richards方程同时具有退化椭圆-抛物型方程的双重特征，因而难以获取解析解［4］；与此同时，土壤水分特征曲线及边界条件的高度非线性，使其数值解的稳定性和质量守恒问题难以完全解决［4-6］。

研究认为，θ型Richards方程严格遵循质量守恒，并在干湿交替的大气边界条件下，相比h型Richards方程有更高的求解效率和数值稳定性［7］，但这类方程难以准确刻画非均质及饱和土壤中的水流运动过程，限制了其发展；另一方面，由于水头在饱和-非饱和非均质土壤剖面中连续可导，h型Richards方程不存在上述困难，但这类方程往往难以保证质量守恒［8-9］；直至Celia等［10］对质量项进行修正后，传统h型方程得以大量应用于Picard迭代模型中，著名的例子有HYDRUS［11］和SWAP［12］软件等。即便如此，h型方程的求解效率在处理干湿交替问题时仍然远低于θ型方程［13］，且常常出现收敛困难等不稳定现象，导致了水盐运移模拟的低效率和低精度问题。为了结合两种单一变量方程的优势，人们提出了传统的主变量转换方法［14］，它基于Newton-Raphson迭代，既能利用h型方程对饱和-非饱和非均质问题的准确刻画，又能保留θ型方程带来的严格质量守恒。但由于需要准备高阶偏导的Jacobian矩阵，Newton-Raphson迭代算法在数学推导及代码实现上更为困难；此外，在节点接近饱和状态时，这类方法容易因主变量非平滑转换出现错误解［15］，因而数值稳定性有待提高。相比之下，Picard迭代算法具有代码简单、数值稳定等特点［9，16］；同时，在该迭代算法框架下进行θ和h型方程（或主变量）的切换，能更为简便地结合两类Richards方程的数值优势，但目前少见报道。究其原因，一方面是广义θ型Richards方程对非均质及饱和土壤的处理［13］尚未广泛得到应用，另一方面是方程层面的切换难以避免在每个临界面两侧新增两个未知变量，从而无法简单通过共同的方程矩阵进行求解。

针对以上两个难题，本文提出一种通用的方程切换方法，它适用于Picard和Newton-Raphson等所有主流迭代求解算法，并能根据每个节点的水分状态进行方程的自由选择：当节点饱和度大于临界阈值时，其控制方程选为h型Richards方程；否则切换为θ型。为实现本文方法，采用广义θ型方程解决土壤非均质问题，并采用h型方程解决土壤饱和问题；同时，采用隐式数值格式来进行交界面上不同控制方程的节点之间的水量平衡分析。本研究以Picard迭代算法为例，成功将该方法应用到一维饱和-非饱和水流运动及溶质运移数值模型方法中。通过室内和数值试验，验证了本文模型相比传统方法（HYDRUS-1D）的优势，并论述了该方法在区域饱和-非饱和土壤水分运动及溶质运移模拟中所具有的应用前景。

2 饱和-非饱和水流运动及溶质运移模型

2.1 水流运动方程不考虑土壤骨架及水流的可压缩性，一维饱和-非饱和土壤水流运动须满足质量守恒方程：∂θ/∂t=-∂q/∂z+s。式中，θ为土壤体积含水量，cm3· cm-3；t为时间，min；z轴以向下为正，cm；s为源汇项，min-1；q为达西通量，cm·min-1，可以用压力水头h或含水量θ两种形式表达：q=-K·∂h/∂z+K=-D·∂θ/∂z+K，式中，K为土壤水力传导度，cm ·min-1；D为土壤水力扩散度，cm2·min-1，D=K/C，其中C=∂θ/∂h为土壤容水度，cm-1。用Φ表示方程切换时采用的主变量（θ或h），则Richards方程的通用表达式为：

当Φ=h时，当Φ=θ时，。式（1）的初始条件可表示为Φt=0=Φ0，其一类（Dirichlet）边界表示为同时，二类（Neumann）边界表示为其中，Φ0为主变量在初始时刻的取值，Φ1为边界上的指定主变量解；qw为边界上的指定通量。

2.2 溶质运移方程一维对流-弥散方程可以表示为：

式中，J=-θDz·∂c/∂z+qc为溶质通量，g·min-1· cm-2；c为溶质浓度，g·cm-3；R=1+ρκηcη-1/θ为迟滞系数，无量纲；Λ=μwθ+μsρκcη-1为一阶反应项，g · cm-3· min-1；Γ=γwθ+γsρ-scs为零阶反应项，min-1；Dz为纵向弥散系数，cm2· min-1，θDz=DL|q|+θDdτ。ρ为土壤容重，g · cm-3；μw、μs分别为一阶反应项的液相和固相反应速率，min-1；γw、γs分别为零阶反应项的液相（g·cm-3·min-1）和固相（min-1）反应速率；s为式（1）中的源汇项，min-1；cs为根系吸水带走的溶质浓度，mg·cm-3；DL为轴向机械弥散系数，cm；Dd为离子（或分子）扩散系数，cm2·min-1；τ为孔隙扭曲度，无量纲，τ=κ为用于线性拟合溶质在溶解-结晶平衡相态的经验常数，cm3·g-1；η为Freundlich等温吸附经验系数，当η=1时为线性吸附，否则为非线性。本文仅讨论线性吸附的情况，因而式（2）为线性方程。初始条件表示为c（x，t）|t=0=c0（x），一类（Dirichlet）边界表示为二类（Neumann）边界表示为其中，c0为初始溶液浓度，c1为边界Ss1上的指定溶质浓度，Q为边界Ss2上的指定溶质通量。

3 方程切换方法

3.1 方程切换临界阈值传统主变量转换方法往往采用若干个经验系数来判断节点水分状态是否满足主变量转换的要求［15］。本文提出用临界有效饱和度Secrit作为阈值来切换每个节点的控制方程。土壤在Secrit时，具有最大容水度C，即当土壤水分变化Δθ时，其负压变化Δh最小，由土壤水分条件强烈非线性变化而引入的数值不稳定最小，此时满足∂C/∂h=0。

以van Genuchten模型［3］为例，定义土壤参数p，它包括土壤残余含水量θr（cm3cm-3），土壤饱和含水量θs（cm3·cm-3），表征土壤级配分布的参数α（cm-1）和无量纲参数n和m=1-1/n，以及饱和土壤水力传导度ks（cm·min-1）。在节点饱和度为Secrit时，压力水头为hcrit|∂C/∂h=0=-m1-m/α，从而得到方程切换临界阈值Secrit=（1+m）-m。其中，m和α对应为节点上的土壤参数。在每一个时间步Δtj内，当节点饱和度小于Secrit时，其控制方程为θ型方程；反之，则选择h型方程。当不存在极大容水度时（例如Brooks-Corey模型［17］等），可以根据土壤类型进行经验取值，例如Secrit=0.4～0.9。

3.2 混合单元水量均衡分析对于相邻节点n和n+1（如图1），当（Sen-Secri）t（Sen+1-Secri）t＜0时，二者控制方程将不再一致，将该节点间的单元称为“混合单元”，编号为n+1/2。混合单元的控制节点控制方程分别为θ和h型。由于两类Richards方程离散节点间水流通量存在内在差异，本文采用和表示节点通量的两种形式，将二者的加权平均作为混合单元内的节点间通量

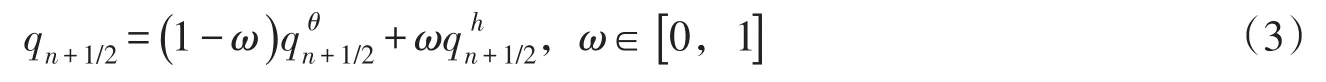
式中，Δzn+1/2为单元n+1/2的空间长度。式（4）是主变量转换和方程切换算法中，单元内节点间通量的通用表达式：当每个单元顶点为θ型方程时，ω=0；当均为h型方程时，ω=1；当两个顶点控制方程不一致时，0＜ω＜1。本文采用算术平均方案，取ω=0.5。

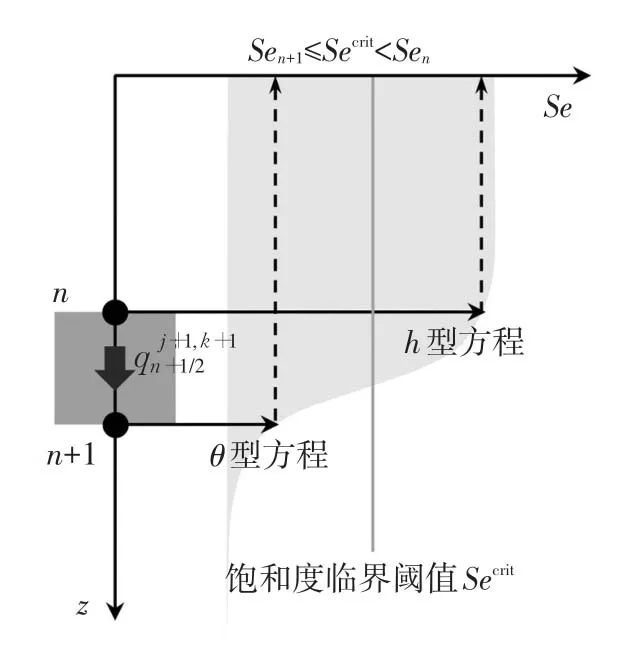
图1 节点n和n+1的方程切换原则及单元n+1/2内节点间通量示意图

特别地，基于Newton-Raphson迭代的传统主变量转换方法［14］可以认为是式（4）的一种特例，其满足ω=1，且各水力参数及未知变量均用主变量的一阶偏导来表示，例如其中，上标j和k为时间和迭代层数（下同），其数学推导不再赘述。为克服前述Newton-Raphson迭代在处理主变量转换时存在的数值不稳定，本文从Picard迭代出发，采用一种半隐格式来求解式（4）。便于简洁，用来表示节点的导水度。

由于非均质界面上节点含水量不连续且不可导，传统θ型Richards方程及式（4）均不适用于处理节点n或n+1处于土壤分层界面的情况，因此需要在节点通量qn+1/2上引入一个非均质修正项［13］：

当n节点为h型方程，n+1节点为θ型方程时，单元n+1/2内的节点间通量表示为：

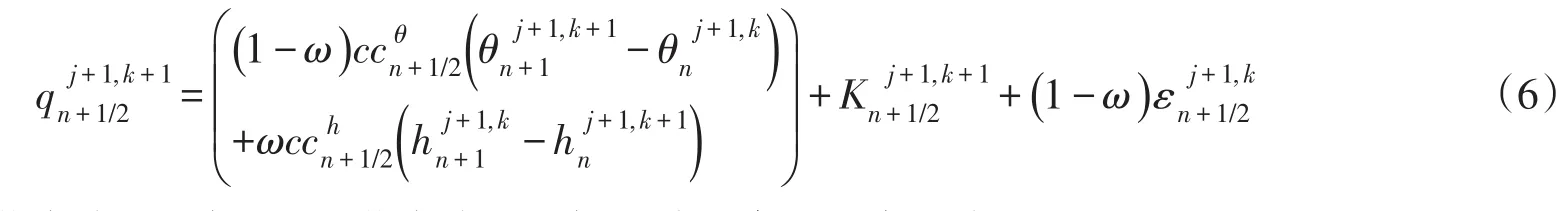
反之，当n+1节点为h型方程，n节点为θ型方程时，该通量表示为：

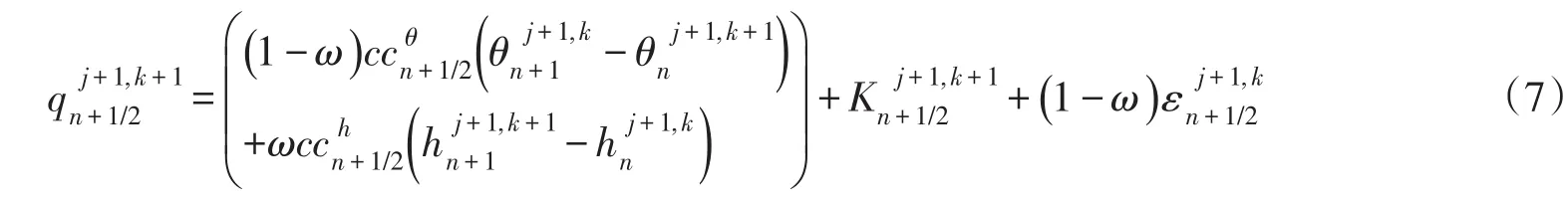
式（6）和式（7）的差异在于混合单元两端未知变量h和θ的显隐格式，可视为Picard迭代算法框架下的混合单元通量表达式。进而我们可以简单地推导出，混合单元n+1/2的Richards方程的空间离散表达式为：为节点n的控制域长度。该式与无切换单元的空间离散格式（参见［15］）保持了一致。

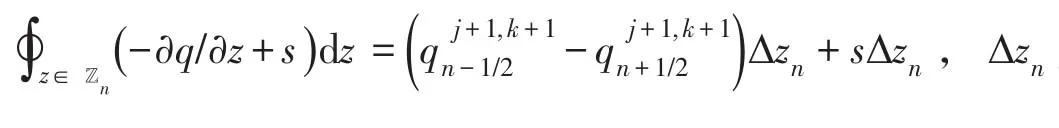
而Richards方程的时间项离散则依据节点方程类型进行：当节点n为θ型方程时，当节点n为h型方程时，采用Celia格式［10］离散时间项：其中，Δtj+1=tj+1-tj为当前时间步长。此外，模型的时间步长自适应和溶质运移方程求解等数值算法均采纳HYDRUS-1D［18］方案，代码编写基于HYDRUS 5.0软件。

4 模型验证及分析

为体现本文方法的数值优势，以经典室内试验来验证本文模型的效率与精度；以土壤水盐运移数值模拟的两个传统方法难以解决的普遍难题为例，证明了本文方法的优势。所有算例以HYDRUS-1D软件的高密度时间和空间网格解Φref为参照解（Φ表示含水量θ、压力水头h或溶质浓度c），得到模型解Φ的均方根误差：

以Em表示不同模型的相对质量误差：

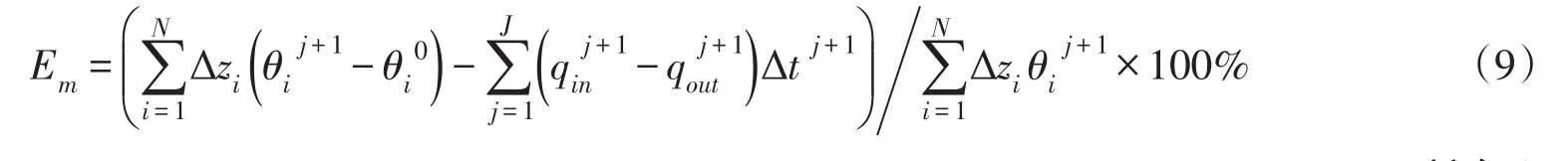
以矩阵求解次数作为通用指标来对比本文方法相比HYDRUS-1D商业软件的计算成本。所有土壤水流运动及溶质运移参数见表1。

4.1 入渗-排水试验为测试本文模型求解水流过程的有效性及模型稳定性，采用经典的Abeele［19］土柱入渗-排水试验进行数值验证。试验采用的一维土柱直径为300 cm，高度为600 cm，填充均质的Bandelier火山凝灰岩（见表1（土壤#1））。试验包括两步：（1）以定水头（htop=0）上边界进行极度干燥条件的土壤强入渗，初始条件为h（z，0）=－729.7 cm，模拟时长5 d；（2）对灌满后的土柱进行为期100 d的自由排水试验观测，上边界密封，设为零通量，初始条件为h（z，0）=0，下边界为（∂h/∂z）bot=0。以网格密度Δz=5 cm、Δtmax=0.5 d的HYDRUS-1D和本文模型解进行对比。其中，HYDRUS-1D软件求解方程 次，本文模型求解方程 次，计算成本节约19%。分析其压力水头和含水量剖面（见图2a），认为模型水流计算的求解精度较高且数值稳定。试验排水阶段水流条件较为温和，采用本文模型及参照模型解对比观测值，得到图2（b）所示土壤含水量剖剖面随时间的变化。本文模型求解非稳定水流过程的精度较高，对比高密度时空网格参照解θref，其RMSE（θ，t）＜0.002 cm3cm-3。

表1 土壤水流运动及溶质运移参数

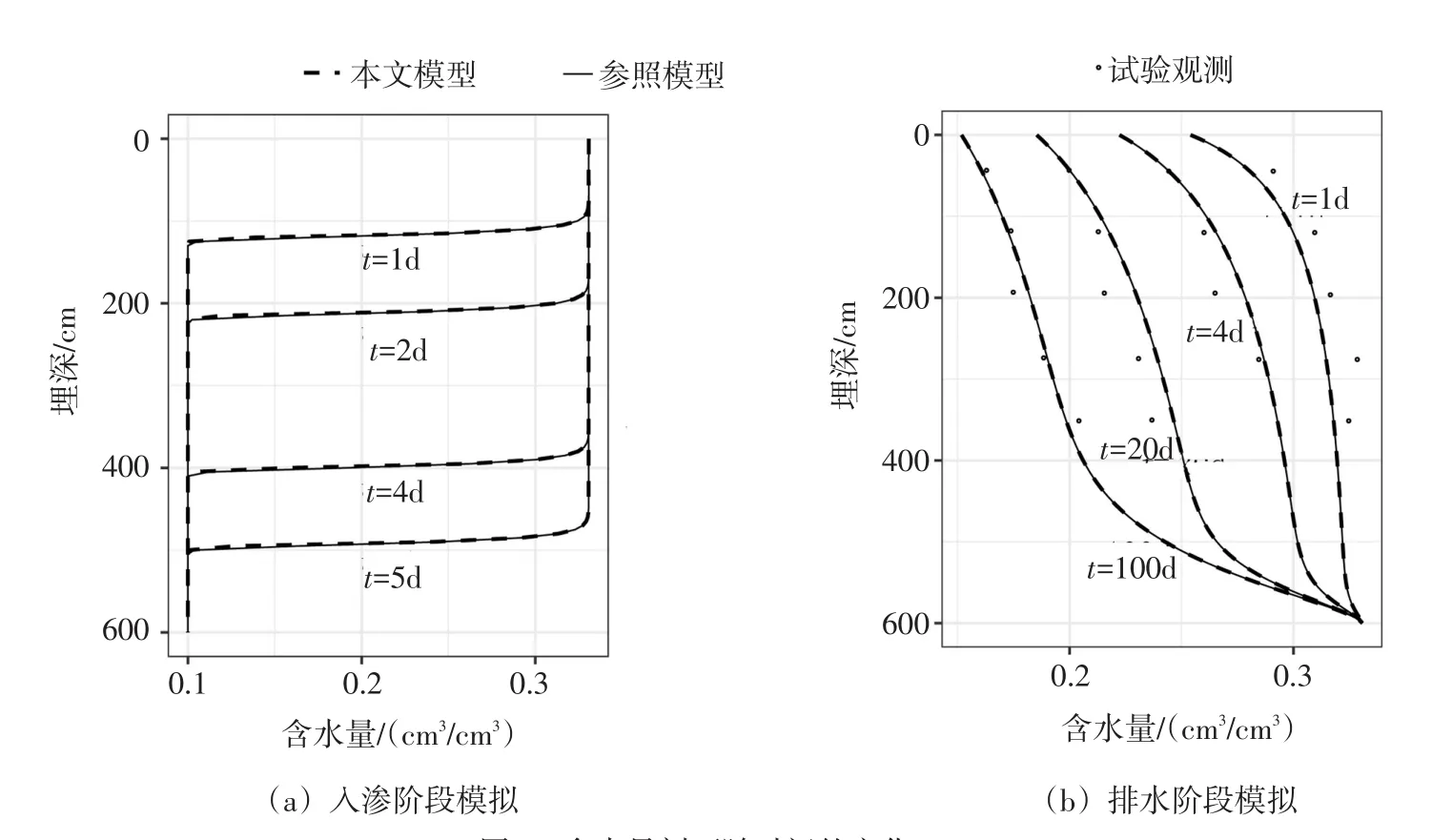
图2 含水量剖面随时间的变化

4.2 镁离子（Mg2+）穿透试验为验证本文模型溶质运移模块的计算精度，以经典的（a）Selim非线性吸附试验［20］和（b）Lai&Jurinak线性吸附试验［21］为参照，进行稳定流状态下的溶质运移模拟。相关参数见表1（土壤#2和#3）。以HYDRUS-1D软件的高密度网格（Δz=0.025 cm、Δt=0.1 h）作为参照解。试验（a）采用0.271 cm/h稳定通量的饱和CaCl2溶液（5 mmol/L）的10.75 cm土柱，在模拟初始的358.05小时内，注入14.26倍孔隙体积量的MgCl2溶液脉冲（5 mol/L），随后恢复注入原始浓度的CaCl2溶液。采用非线性吸附函数模拟镁离子的交换过程，整个试验持续600小时。试验（b）则采用2.64 cm/h稳定通量的CaCl2溶液（125 mmol/L）的25 cm土柱，在初始的3.9小时内，同时注入两份各62.5 mmol/L的MgCl2和CaCl2溶液，随后恢复注入原始浓度的CaCl2溶液。采用线性吸附函数模拟镁离子的交换过程，整个试验持续30 h。两个镁离子穿透试验的数值模型上边界为定溶质通量边界（二类边界）：下边界为零梯度自由边界：在土柱底部进行镁离子浓度检测，得到如图3所示，本文模型的溶质运移模块计算结果准确，RMSE（c，t）＜0.005 mmol/L。

4.3 砂土淋盐过程模拟本节参考Miller经典算例［22］，模拟干旱灌区厚包气带淋盐过程，设置均质土柱高度为1000 cm，土壤参数见表1（#2）。初始条件为静水压状态，潜水面位于柱子底部（即h（z，0）=z-1000 cm）。在地表0～10 cm埋深处，存在均匀分布的高浓度盐分20 g/L，其它埋深盐分背景值为0.5 g/L。模拟过程中，上边界以定水头htop=0 cm进行淋盐，灌溉水质0.5 g/L；下边界为定水头hbot=10 cm，地下水盐分浓度为2 g/L，全部淋盐过程持续260 min。主要溶质运移参数见表1中土壤#4。算例在t=80 min、160 min、260 min处获取观测剖面，对比高密度网格（Δz=0.25 cm）的HY⁃

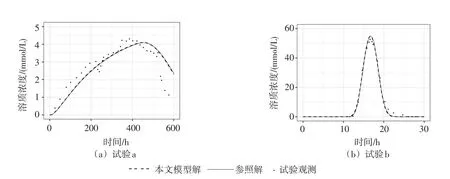
图3 镁离子穿透曲线

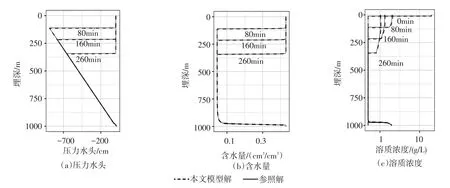
图4 压力水头、含水量和溶质浓度剖面随时间的变化

DRUS-1D模型解，得到如图4的（a）压力水头、（b）含水量和（c）盐分浓度剖面随时间的变化情况。

采用网格分辨率为Δz=0.5 cm、1.0 cm、1.25 cm和2.0 cm的本文模型及相应网格密度的HY⁃DRUS-1D解对比高密度网格参照解，得到图5所示盐分浓度、土壤含水量剖面解的RMSE随时间的变化。总体上，本文模型能保证不同网格分辨率上更高的求解精度。对于网格密度为Δz=0.5 cm、1.0 cm、1.25 cm和2.0 cm的情况，本文模型相比HYDRUS-1D软件，分别节省了16.8%、21.2%、12.8%和7.1%的计算成本，压力水头解的求解误差降低了8%～79%，含水量求解误差降低了3.5%～60%，溶质求解误差降低了9.6%～43%。因而在保证更高计算精度的同时，能实现更高效率的求解。以Δz=1.0 cm为例，HYDRUS-1D软件则需要求解方程10499次，总体质量误差为0.234%；而本文模型求解方程次数为8270，质量误差为7.25×10-5%，节省了21%以上的计算成本，降低了99.97%的质量误差。从算法稳健性来看，本文模型能适应更大的时间步长，及更高密度的网格。自适应时间步长方案下，本文模型最大时间步长是HYDRUS-1D软件的1.20～1.44倍，最小时间步长则为后者102～104倍，从而明显节省计算工作量；而在更高密度网格下，本文模型能更大幅度地提高计算精度。

4.4 干湿交替的地表积盐过程模拟非均质土壤的水流运动过程具有强烈非线性，通常对数值工具的稳定性及计算效率有更高的要求。传统基于θ型Richards方程的方法往往因为无法准确计算饱和土壤及非均质界面处的节点间通量而少见应用；同时，基于h型Richards方程的模型，例如HYDRUS和SWAP系列软件，往往在干湿交替的大气边界上具有较低的计算效率甚至无法正确求解，此外容易造成较大的质量误差［13］。针对这个问题，本节参照Hills经典问题［23］，进行干湿交替的大气边界下，我国北方干旱-半干旱灌区非均质土壤的积盐过程模拟。将高度为1 m的土柱均匀分为5层（每层20 cm），自上而下，在第1、3、5层中填充均质细砂土（见表1中土壤参数#5），在2、4层中填充均质黏壤土（见表1中土壤参数#6）。在初始状态下，土柱水头均匀分布，h（z，0）=-100 cm，初始盐分背景浓度为c（z，0）=1.5 g/L。下边界指定水头和盐分浓度：hbot=0、cbot=1.5 g/L；考虑复杂的干湿交替大气边界（见图6）。上边界溶质输入量近似设为0.5 g/L。算例对比相同网格密度（Δz=1 cm）下的HYDRUS-1D软件及本文模型的计算效率与精度。模拟时长365天。由于高密度网格时HYDRUS-1D软件难以收敛，因而本算例以相同网格密度下的HYDRUS-1D软件解作为参照解。

图5 对比砂土淋盐数值求解剖面溶质浓度、含水量的RMSE

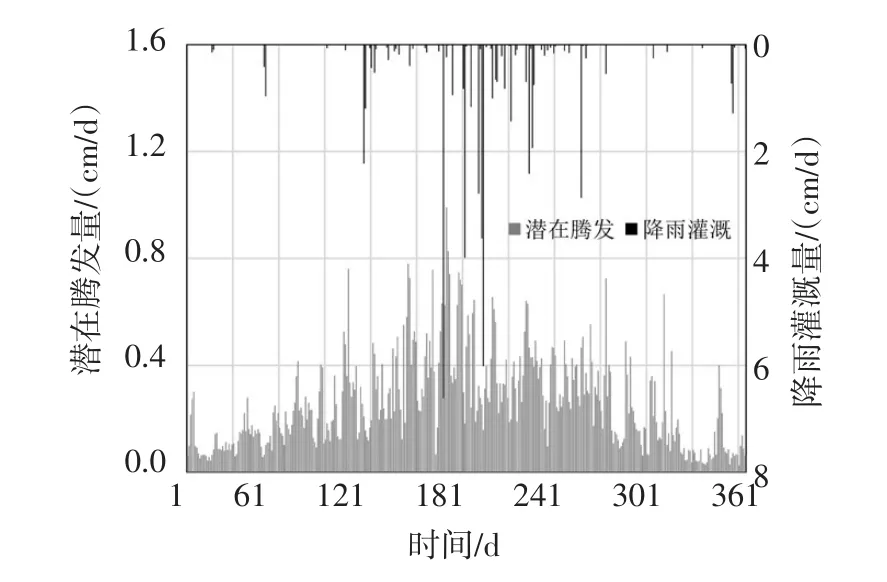
图6 干湿交替的大气边界

在干旱地区，大量的潜在腾发将造成土壤积盐（见图7（a）），尤其是地下水位较浅的情况。本文以虚拟算例为例，模拟了这种积盐过程。图7（b）为位于z=10 cm（砂土层）的观测点上，盐分的变化过程。当出现短时间的降雨或灌溉入渗时，土壤盐分得到迅速淋洗，但由于强烈、持续的腾发作用，这种积盐过程再次发生。通常认为，干湿交替的大气边界模拟容易造成基于h型Richards方程的数值模型（如HYDRUS、SWAP等）出现较大幅度的数值振荡。尤其当土壤较干燥时，少量的水分输入往往导致压力水头在多个数量级上发生变化，因而模型需要更多的迭代来完成一次求解。但对于θ型方程而言，干湿交替使得含水量θ在一个时间步内的变化幅度不超过θs～θr。本文模型以10 s完成计算（方程求解9293次），而HYDRUS-1D则耗时606 s（方程求解699698次），本文模型节省98%以上的计算成本。值得一提的是，为获取更高精度的数值解，本文方法能高效求解更高密度的数值网格，例如，Δz=0.1 cm时，计算耗时107 s，而HYDRUS-1D的计算则因不收敛而中断。对比相对质量守恒误差，本文模型（1.4×10-3%）相比HYDRUS-1D软件（7.5%）而言，质量误差减小99.98%。

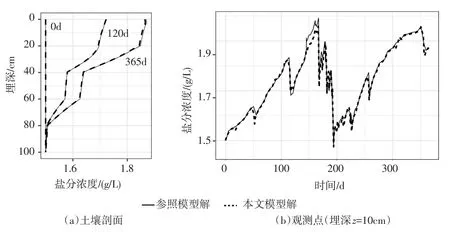
图7 盐分浓度随时间的变化

5 结论

针对传统土壤水分运动数值模型存在数值振荡、质量误差大等潜在问题，本文提出一种通用的控制方程切换技术，并成功应用于一维非均质饱和-非饱和水流运动及溶质运移数值模拟中。通过一系列室内及数值试验，认为本文模型能获得有效的数值解。对比通用软件HYDRUS-1D，本文模型经论证实现了数值精度的普遍提升。采用经典数值算例，讨论了传统数值方法难以解决的两个普遍问题：（1）在干燥砂土淋盐问题中，本文模型能在更大的时间步长下克服传统水流模型难收敛的问题，并证明了基于方程切换技术的数值模型在计算精度上有显著提升。其中，计算成本节省7.1%～21.2%，压力水头误差减小8%～79%，含水率误差减小3.5%～60%，溶质误差减小9.6%～43%，质量误差减小99.98%。（2）在大气边界干湿交替条件的非均质土壤积盐问题中，本文模型能大幅降低计算成本，并能在更高密度的网格下快速获取高精度解（此时HYDRUS-1D软件难以收敛）。本文提出的通用方程切换技术能应用于二维、三维水流运动及溶质运移模型中；对于大区域水流运动与溶质运移模拟，本文模型能实现高效率数值求解。