黄河宁蒙河段冰期洪水波运动过程中的变形分析

王恺祯，王 军，隋觉义

（1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009；2.北英属哥伦比亚大学 环境工程系，加拿大 乔治王子城 V2N 4Z9）

1 研究背景

特殊的地理位置和气候条件使黄河宁蒙河段每年凌汛期（当年11月至次年3月）发生不同程度的凌情［1］，冰凌会危及桥梁、涵洞、河道工程和其他水工建筑物的安全［2-3］。在封、开河时期，如果冰凌严重堵塞河道，造成水位大幅度地抬高而引发漫滩或决堤，会给黄河滩区和两岸人民群众的生命财产安全带来威胁和损失，准确及时的凌汛预报能够为防汛工作提供决策支持。

处于稳定流状态的河道水流，由于暴雨径流、水电站运行或闸坝放水等原因，使原来的水面受到干扰而形成不稳定波动，即洪水波，波流量从河道上游向下游运动，就产生了河道里的洪水波运动。洪水波在演进过程中会发生变形［4］，生产实际中，洪水波的传播机制是洪水预报、防洪规划和水利工程防洪控制运用中重要的组成部分，其研究具有重要的理论和实际意义。

目前广泛应用于洪水波的传播计算的马斯京根法由McCarthy于1938年应用于美国马斯京根河流域而得名，后经一系列研究，到1978年Pouce和Yevjevich将变动水面宽度及动力波速度的变动参数应用于1969年Cunge提出的马斯京根-康吉模型［5］上，马斯京根模型此时才基本完善。该方法在实际应用中的一个重要问题是模型参数的估计。在传统方法中，利用试算法对参数K、x进行率定，再计算出决策变量C0、C1、C2，但是试算法具有盲目性、不确定性等缺陷，因此有学者选择了直接优化决策变量C0、C1、C2，得到较好的效果，主要方法有最小二乘法［6］，遗传算法［7］，粒子群算法［8］等。马斯京根法的参数K反映洪水波的传播时间，而x则反映河段蓄量的大小及调蓄能力。

对于洪水演进，可采用水力学的非恒定流法和水文学的马斯京根法来计算。当河流有冰存在时，由于冰水存在能量、质量交换，使得计算难度加大，而马斯京根法可以从水量平衡方程中考虑到冰水量的相互转化问题，本文拟应用马斯京根法对冰期冰盖下洪水波的变形进行尝试性研究计算。

2 考虑有冰存在的马斯京根法

在水文循环过程中，任一区域、任一时段内输入水量与输出水量之差等于其蓄水量的变化量，根据质量守恒定律可写出某一区域任一时段（Δt）内的水量平衡方程：

冰期进行水量平衡计算时，若忽略上游水流向下游传播过程中转化为冰的水量，以及上游冰盖或浮冰消融流入下游水流中的水量，而完全使用水量平衡方程的一般公式，则会增大下游断面计算流量的误差，考虑冰量存在的水量平衡方程应为：

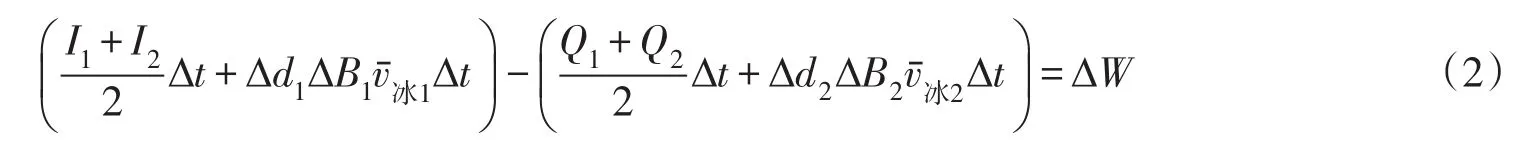
式中：I1、I2为上游断面时段始、末流量，m3/s；Q1、Q2为下游断面时段始、末流量，m3/s；Δt为所取的计算时长，s；ΔW为时段槽蓄水量的变化量，m3；Δd1、Δd2为上、下游断面冰盖厚度的变化值，m；ΔB1、ΔB2为上、下游断面冰盖宽度的变化值，m；vˉ冰1、vˉ冰2为上、下游断面冰盖下的平均流速，m/s。

天然河道洪水波运动的动力方程为：

式中：Z为水位，m；L为河段长，m；v为断面平均流速，m/s；g为重力加速度，m/s2；为水面比降；Sf为摩阻项，用曼宁公式计算；为惯性项。式（3）是以牛顿第二定律为基础建立起来的，反应了能量守恒，对于一般的天然河道水流，动力方程中惯性项较其他项要小两个数量级，通常忽略。对无旁侧入流的冰期河段，忽略惯性项，式（3）可写成：

式中：vc为冰盖下过水断面的平均流速，m/s；C为谢才系数；Rc为冰盖下过水断面的水力半径，m；nc为冰盖下的综合糙率，其计算方法参见文献［9］。

冰盖生成时，水流的流动结构发生显著的改变，一般以最大流速线将流动沿水深方向分为冰盖区和床面区两层，对于概化的矩形断面，床面区湿周χb=b+2H，冰盖区湿周χi=b：

冰期河槽蓄水量Wc为

式中：H为冰盖下流动的水深，m；b为断面宽，m；Ac为冰盖下过水断面面积，m2；为冰盖下平均过水断面面积，m2；为冰盖下平均流动的水深，m。

将式（8）代入到式（7）后得）

可写成函数形式

假定冰期槽蓄水量Wc和入流量Ic、出流量Qc存在线性关系，马斯京根法在忽略惯性项下的槽蓄方程为：

式中：Jc为冰期断面的水力坡度；K和x为马斯京根法的流量演算参数，K值等于在相应蓄量下恒定流状态的河段传播时间，K值越小，洪水波传播时间越短，反之越长；x是反应河槽调节作用的一个指标，即反应洪水波传播过程变形的程度，x减小，洪水波变形增加，反之减少。

进一步分析K、x和糙率的关系，K的计算公式为：

明流时期，概化的矩形断面洪水波波速c与断面平均流速v的关系为［10］：

由曼宁公式及式（13）、式（14）可以推出明流时期K的计算公式为：

x的计算公式为［11］：

稳定流流量Q0的计算公式为［12］

由曼宁公式及式（13）、式（14）、式（16）可以推出明流时期x的计算公式为：

式中：H0为相应的稳定流水位，m；J为明流期时断面的水力坡度；n为河床糙率系数；Qb为基流流量，m3/s；Qp为洪峰流量，m3/s。

由式（15）、式（18）可知，K值与糙率成正比，x与糙率成反比，即糙率越大，洪水波传播时间越长，洪水波的变形越大。

3 宁蒙河段冰期马法计算验证

如图1所示，宁蒙河段地处黄河流域最北端，从宁夏的石嘴山市和内蒙古伊克昭盟的拉僧庙入境，至伊克昭盟准格尔旗马栅的榆树湾出境，干流全长840 km，总落差162.5 m。河道流向从石嘴山至巴彦高勒为由西南流向东北，巴彦高勒至包头市为自西向东，包头市至清水河县的喇嘛湾为由西北流向东南，喇嘛湾至出境为由北向南［13］。

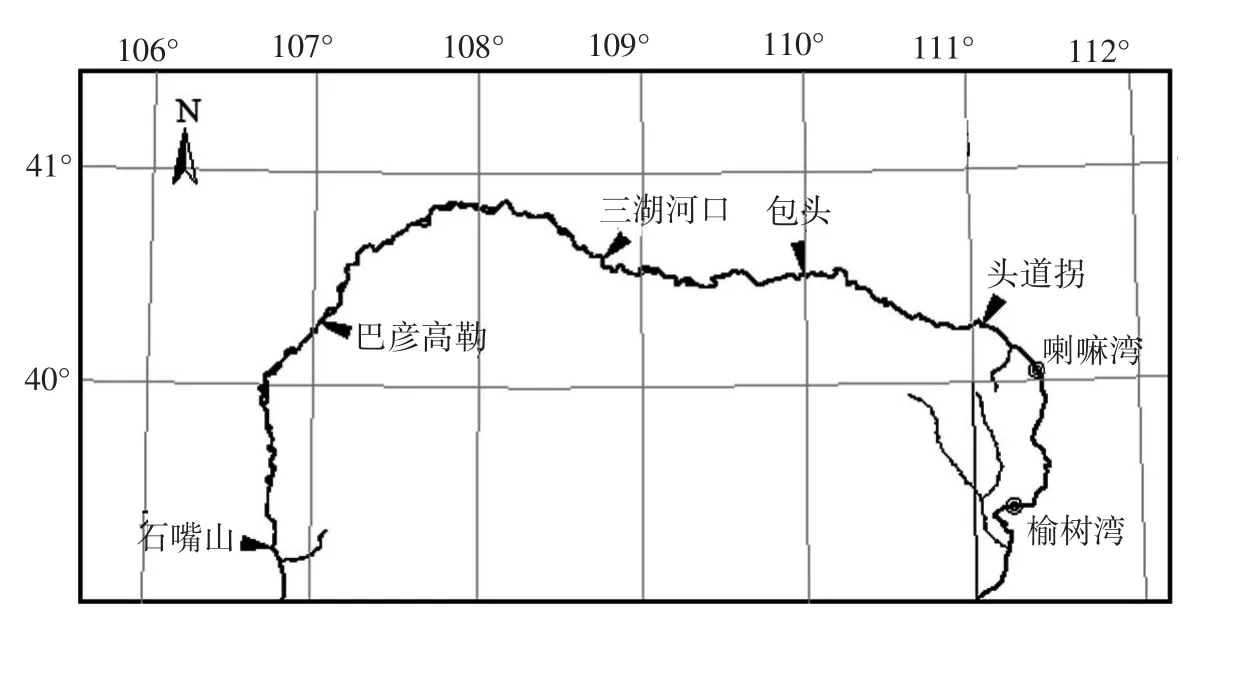
图1 宁蒙河段示意图

图2 开河期流量特性

选择黄河宁蒙河段的巴彦高勒（东经106°02'，北纬40°19'）、三湖河口（东经106°47'，北纬40°36'）、包头（东经109°55'，北纬40°32'）、头道拐（东经111°04'，北纬40°16'）为研究的水文测站，采用2014—2016年流量数据进行计算分析。

图2（a）为2015年包头和头道拐水文站开河期的流量过程线，下游头道拐水文站比上游包头水文站提前4天半开河，其流量过程出现了两场比较大的洪水，前一场洪水由下游提前开河时槽蓄水量的释放形成，洪水呈“尖瘦”状；后一场洪水由上游开河，槽蓄水量向下游传播形成，洪水形状相对前一场较“矮胖”，洪量更大。图2（b）为2016年包头和头道拐水文站开河期的流量过程线，上游包头水文站先于下游头道拐水文站开河，洪峰演进过程沿程增大，上下游洪峰间隔时间沿程减小。

选取稳封期到开河期前夕、开河期、明流期三个计算时期，应用最小二乘原理进行马斯京根法参数K、x的最优估计，并对其计算值的可靠性进行验证，对流量过程、洪峰流量及洪量进行误差计算。限于篇幅，对于流量过程的演算仅列出三湖河口-包头河段，如图3所示。

图3 包头断面演算流量与实际流量过程对比

从数值上分析流量误差，稳封期到开河期前夕的误差小于明流期的误差小于开河期的误差，计算值与实测值的数值和趋势皆比较接近，流量演算拟合程度高，洪峰流量和洪量的误差及确定性系数的计算结果如表1所示。

从确定性系数上看，马斯京根法计算下的明流时期高于有冰存在的两种情况，有冰存在的确定性系数最小为0.793，仍比较高，故认为将马斯京根法应用于冰期是可行的。

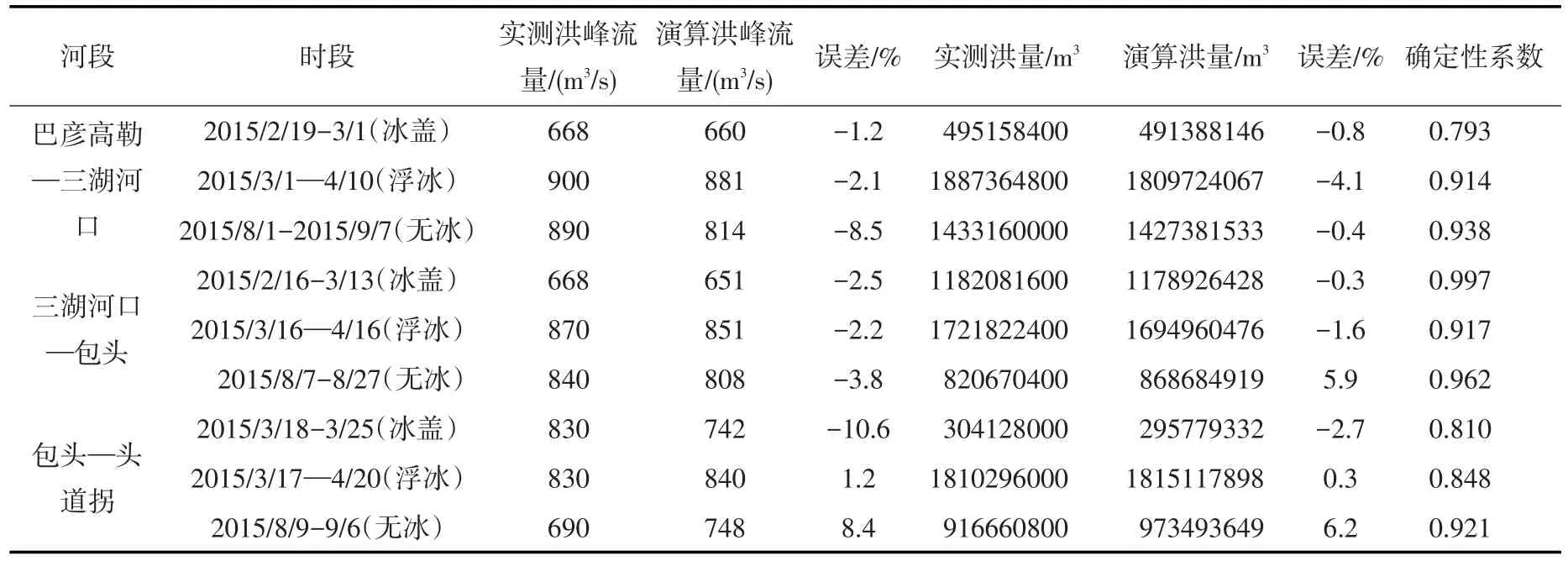
表1 洪峰流量及洪量的误差分析

4 封冻期洪水波传播变形分析

将封冻期冰盖的发展过程分为两部分，以冰盖达到最厚为临界点，从初封到冰盖达到最厚视为冰盖的冻结增厚过程，冰盖从最厚到瓦解消融视为冰盖的融化减薄过程。参数x能够间接反映洪水波传播的变形，对任一时段，可通过马斯京根方程求出参数x值，以及同时段的平均冰厚值d，从而建立参数x与平均冰厚d的散点关系图。

根据2013—2017年封冻期的流量及冰厚数据进行计算。每隔5～6 d建立一组马斯京根法的流量方程，一组方程能够求解得到一个x值。计算时对流量进行内插，时间间隔取Δt=8h，冰厚d取时段始末的均值。冰盖冻结增厚时期参数x与平均冰厚d的散点关系图如图4所示。

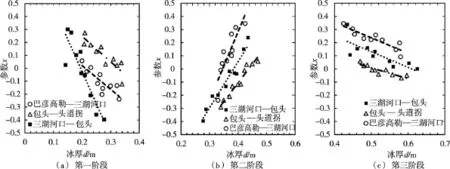
图4 冰盖冻结增厚过程参数x与冰厚d关系

冰盖的冻结增厚过程对洪水波变形的影响可分为3个阶段。图4（a）为第一个阶段，冰盖处于初封期，冰盖的增厚使洪水波变形增大，这一阶段冰盖增厚速度在0.01～0.03 m/d，巴彦高勒-三湖河口段的计算冰厚范围在0.25～0.33m，三湖河口—包头段的计算冰厚范围在0.14～0.27 m，包头-头道拐段的计算冰厚范围在0.20～0.34 m；之后进入第二阶段，如图4（b）所示，冰盖的增厚使洪水波变形减小，这一阶段冰盖增厚的速度稳定且缓慢，增厚速度小于0.01 m/d，巴彦高勒-三湖河口段的计算冰厚范围在0.33～0.42 m，三湖河口-包头段的计算冰厚范围在0.27～0.43 m，包头-头道拐段的计算冰厚范围在0.34～0.47m；到了第三阶段，如图4（c）所示，洪水波的变形又相对增大，这一阶段冰厚几乎没有变化，而流量持续增大，气温逐渐上升，有些天数日最大气温已达0℃以上，巴彦高勒-三湖河口段的计算冰厚范围在0.42～0.58 m，三湖河口-包头段的计算冰厚范围在0.43～0.62 m，包头-头道拐段的计算冰厚范围在0.47～0.60 m。

综上所述，在冰厚快速增加的第一阶段，冰盖的出现增大了过水断面的湿周和阻力［14］，河段综合糙率增加，洪水波变形增大；随后在冰厚缓慢增加的第二阶段，由于水力磨蚀作用，冰盖底部渐趋光滑，糙率降低，洪水波变形减小；最后在冰厚几乎不发生改变但流量增大的第三阶段，由于冰厚保持最大值状态，稳封期综合糙率没有大的改变，由式（18）知，Q0与x成反比，流量增大，通过影响Qp，使Q0增大，x减小，故洪水波变形增大。

冰盖融化减薄期参数x与平均冰厚d的关系图如图5所示。

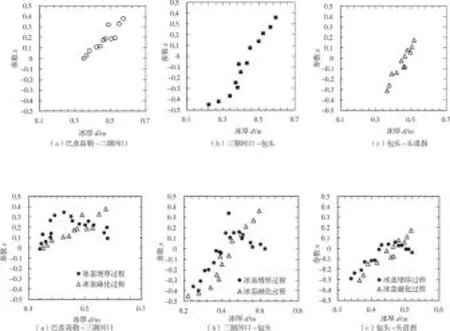
图5 冰盖融化减薄过程参数x与冰厚d关系

冰盖融化减薄的时期，由于冰盖融化至0.35 m以下的冰厚数据极少，故计算范围有限。计算范围内的洪水波变形随冰盖的消融而增大，巴彦高勒—三湖河口段的计算冰厚范围为0.35～0.57 m；三湖河口—包头段的计算冰厚范围为0.22～0.6 m；包头—头道拐段的计算冰厚范围为0.36～0.52 m。

将冰盖冻结增厚和冰盖融化减薄过程对比分析，巴彦高勒—三湖河口段的计算冰厚范围在0.35～0.58 m，三湖河口—包头段的计算冰厚范围在0.22～0.60 m，包头—头道拐段的计算冰厚范围在0.34～0.52 m。计算结果如图6所示。

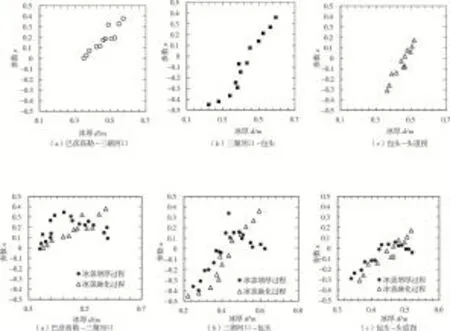
图6 冰盖冻结增厚与融化减薄过程参数x与冰厚d关系对比

冰盖冻结增厚过程和冰盖融化减薄过程下洪水波的变形程度并不一致，且两个过程的参数x均会在冰盖冻结增厚对洪水波传播变形的第三阶段有交点，交点之前的冰厚范围，冰盖融化减薄时的洪水波变形更大，交点之后的冰厚范围，冰盖冻结增厚时的洪水波变形更大。冰厚的计算范围如表2所示。

由于洪水波传播过程的变形程度为水深和冰盖糙率的综合作用，冰盖融化减薄时的洪水波变形更多，说明该冰厚范围内，相同冰厚下冰盖融化减薄过程的冰下过流能力更小；冰盖冻结增厚时的洪水波变形更多，说明该冰厚范围内，相同冰厚下冰盖融化减薄过程的冰下过流能力更大。

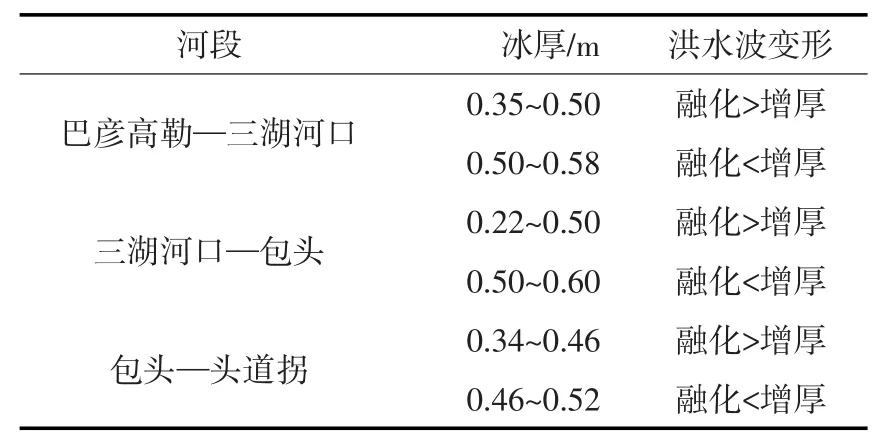
表2 各河段冰厚与洪水波变形分析

5 结论

基于马斯京根法，选取黄河宁蒙河段为研究对象，经过分析，得出以下结论：

通过K、x的计算公式，分析其与糙率的关系，得出K值与糙率成正比，x与糙率成反比，即糙率越大，洪水波传播时间越长，洪水波的变形越大。

对计算出的马斯京根法参数K、x的可靠性进行验证，得出计算值与实测值的数值与趋势皆比较接近，认为将马斯京根法应用于冰期是可行的。

冰盖冻结增厚过程对洪水波传播的影响可分为3个阶段：在冰厚快速增大的第1阶段，断面综合糙率增加，洪水波变形增大；随后在冰厚缓慢增加的第2阶段，断面综合糙率的降低使洪水波变形减小；最后在冰厚几乎不发生改变但流量增大的第3阶段，断面综合糙率没有大的变化，流量的持续增加使洪水波变形增大。冰盖的融化减薄过程，流量持续增加，冰厚的减小使洪水波变形增大。两个过程的参数x均会在冰盖冻结增厚对洪水波变形影响的第3阶段有交点，交点之前的冰厚范围，冰盖融化减薄时的洪水波变形更大，冰下过流能力更小，交点之后的冰厚范围，冰盖融化减薄时的洪水波变形更小，冰下过流能力更大。

致谢：研究工作得到黄河水利科学研究院的大力支持，谨致真挚谢意！