考虑级配效应的堆石料颗粒破碎与变形特性研究

朱 晟，宁志远，钟春欣，楚金旺，高庄平

（1.河海大学 水文水资源与水利水电工程科学国家重点实验室，江苏 南京 210098；2.河海大学 水利水电学院，江苏 南京 210098；3.中国恩菲工程技术有限公司 恩菲研究院，北京 100038）

1 研究背景

堆石料的粒径和级配决定颗粒间的接触关系，进而影响其宏观力学响应。已有研究表明［1-6］，土体的应力应变关系不仅取决于受力状态，还取决于材料密实程度，堆石料的级配性状显著影响材料的物理性质和力学行为。文献［7-12］研究了不同颗粒级配及细粒含量对堆石料渗透性、黏聚力和摩擦角等性质的影响，提出堆石料抗剪强度随不均匀系数Cu的增加而降低的现象。朱俊高等［13］基于离散元方法，发现当颗粒处于相同孔隙率时，由于级配不同会造成相对密实度的较大差别，从而引起摩擦角的变化和剪切性状的不同。赵婷婷等［14］整理了不同级配指标与邓肯模型强度参数（φ0、Δφ），莫尔库伦强度参数（C、φ）、变形参数（E、ν）及密实度指标（n、e）之间的关系，但缺乏相应的物理试验验证。Yan等［15］采用单一粒径的颗粒流试验模拟三轴剪切条件下材料的变形特性，建立了模型常量与级配指标Cu之间的函数关系，从细观角度解释了模型参数的物理意义。现有成果定性表述颗粒材料级配与力学性质参数之间的关系资料较多，能够定量描述并建立函数关系的研究较少，且主要依靠数值试验手段，研究重点集中在细粒含量（小于5 mm颗粒）的影响方面。

堆石料的级配分布、颗粒形状、表面特性及颗粒间的孔隙特性对其密实程度产生直接影响，这些特征在某一尺度范围内均存在随机性及符合统计规律的自相似性，文献［16］研究表明堆石料的颗粒破碎符合分形特征，文献［17-18］通过试验得到了连续粒径体系最紧密堆积的经验曲线即Talbot曲线，满足分形分布。实践也证明，大量工程的堆石体级配基本为分形分布，且基于粒度分形维数进行堆石料的级配设计，可以达到最优压实效果［19-20］。刘映晶等［21］、李罡等［22］和Carrera等［23］研究了粒状材料的级配效应问题。

本文选取堆石料级配的制样分形维数作为反映其结构参数的指标，进行不同级配的室内物理力学试验，结合笔者提出的统一广义塑性模型［24］，研究考虑级配效应的堆石料物理力学性质。

2 试验方案

三轴试验在河海大学LSW-1000大型三轴剪切试验机上进行，试验仪器的主要技术参数为：（1）最大轴向试验力：1000 kN；（2）轴向变形测量范围：0～200 mm；（3）变形速度控制范围：0.5～3.0 mm/min；（4）试验力、围压长时稳定度：±2%。试验时，分别选取4级围压（0.4、0.8、1.6和3.1 MPa）进行饱和固结排水压缩剪切试验。试样直径为300 mm，试样高度为600 mm。制备好试样后，依次进行真空饱和、试样固结和压缩剪切，固结时间不小于2 h，在恒定围压下施加轴向荷载进行压缩剪切，剪切速率控制为1 mm/min。

试验堆石料为弱风化英安岩料，岩石比重2.67，饱和抗压强度55～75 MPa。选取粒度分形维数D制样为2.1、2.48、2.53、2.56、2.70和2.80，相对密度Dr均为0.8的6组不同级配的堆石料试样，其中D制样=2.53级配的三轴试验结果用于验证本文建立级配与力学参数之间的关系。

根据下式计算6组试样的级配曲线

式中：di为各粒组平均粒径；dmax为最大粒径；D制样为试验级配的粒度分形维数。

级配曲线见图1。

3 试验结果分析

根据6组级配堆石料试样的室内相对密度试验结果，试验干密度极值与级配的粒度分形维数可采用下式二次函数较好地拟合

式中，γd为相对密度，g/cm3；a、b、c为试验参数。无论最大干密度（Dr=1.0）还是最小干密度（Dr=0.0），随着粒度分形维数的增加，均呈现出先增加后减小的趋势，最大值出现在D制样=2.6附近，见图2。

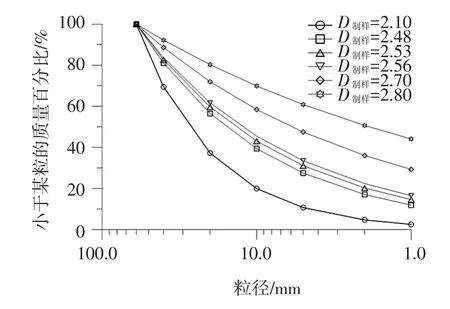
图1 堆石料试验级配曲线

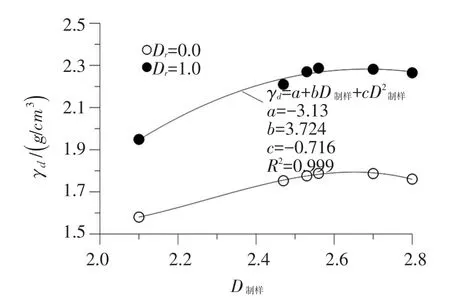
图2 堆石料室内相对密度试验结果

3.1 强度特性与级配的关系6组级配堆石料试样的三轴试验结果见图3，三轴试验剪切破坏时的峰值应力见表1。从图3可以看出，各级配试样达到峰值的偏应力，随着围压的增大而增大，表现出典型的压硬性；随着分形维数D制样的增大，堆石颗粒逐渐变细，除低围压下的极少数峰值偏应力异常外，绝大部分试样均表现出随着D制样的增大，峰值偏应力先逐渐增大，在D制样达到2.6附近时达到极大值，而后又呈现减小的趋势。可见，当D制样在2.60附近时，较优的颗粒充填关系，使得干密度最大，堆石料抗剪强度也最高。

为了进一步研究堆石料的强度与级配之间的关系，将分形维数D制样与峰值偏应力qf的关系绘于图4（a），堆石体的峰值偏应力qf与平均应力p的关系绘于图4（b），并采用式（3）计算堆石体的抗剪强度参数［24］，见表2。

图3 堆石料室内大型三轴试验曲线

表1 堆石料三轴试验破坏应力 （单位：kPa）

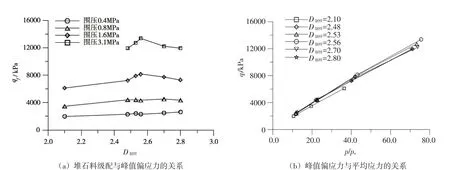
图4 堆石料的抗剪强度曲线

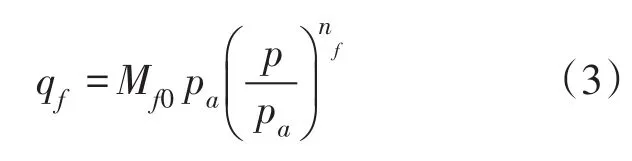
式中：qf为峰值偏应力；pa为大气压；p为平均主应力；Mf为破坏应力比；nf为反映静水压力影响程度的材料常数。

为建立堆石料的抗剪强度参数和级配之间的关系，将表2数据绘于图5，并经回归分析可知，Mf0～D制样之间较好地符合二次函数关系，D制样～nf则基本呈现线性关系，可分别采用式（2）和式（4）较好地拟合。

式中：a1、b1为拟合参数。为了解堆石料试验过程中的颗粒破碎情况，分别对3个级配试样D制样=2.48、2.56和2.59在4组围压下的试验结束后进行了筛分，结果见图6。

根据式（1），计算试验破碎后各筛分级配的分形维数D破碎，得到与级配、围压的关系，见图7。对于不同制样级配的破碎分形维数D破碎与围压的关系，可用下式拟合

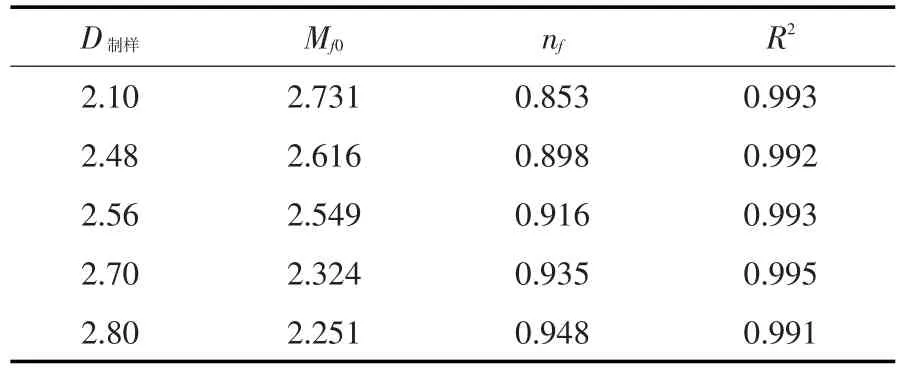
表2 不同级配堆石料的抗剪强度参数

图5 堆石料级配与抗剪强度参数的关系

其中，拟合参数值a2、b2见图7。将式（5）参数a2、b2与D制样，绘于图8，可以看出两者基本呈直线关系，将a、b与D制样的直线方程式代入式（5），得到：

由式（6）可知，三轴试验中堆石料颗粒破碎程度，取决于制样级配的粒度分形维数和围压。对于同一级配而言，围压越高，D破碎越大，颗粒破碎越明显。对于同一围压而言，D破碎越大，细粒含量越高，颗粒破碎率越小，由式（4）可知，参数nf越接近1.0，围压对抗剪强度的贡献越大。

3.2 剪胀特性与级配的关系堆石料的剪胀特性，模型［24］通过如下剪胀方程反映：

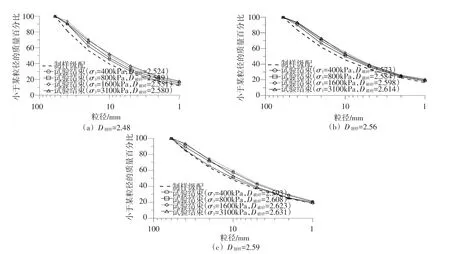
图6 三轴试验前后的级配曲线

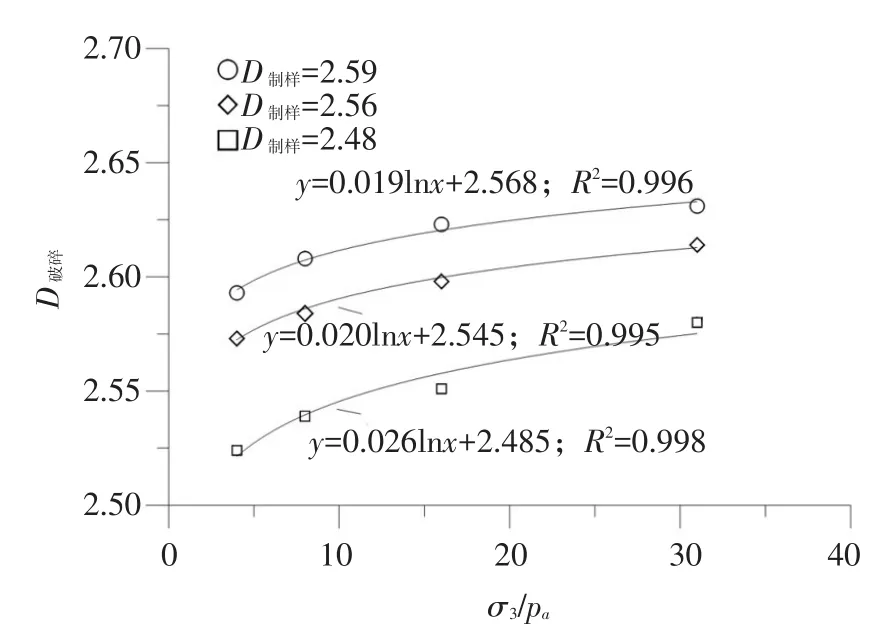
图7 堆石料破碎分形维数与制样分形维、围压的关系

图8 堆石料破碎分形维数与参数a2、b2的关系

式中：dg为塑性体积应变增量与剪切体积应变增量之比；α、β、Mc为模型参数，相应的物理意义见图9，Mc为剪胀与剪缩变相点的应力比；α为图中剪胀线直线段的斜率；β定义了等向压缩情况下曲线开始趋向无穷大时与η=0轴的距离；η为应力比，η=q/p。

5组试验级配的试验剪胀应力比Mc见图10，剪胀应力比可用直线q=Mcp表述。剪胀比Mc随D制样的变化关系曲线见图11，Mc和D制样两者关系同样可用式（2）的二次函数较好地拟合，可见，随着粒度分形维数的增加，颗粒平均粒径逐步减小，细粒含量逐步增加，Mc表现出单调递减特性，三轴试验中堆石料出现剪胀效应的平均应力越来越低，试样的剪胀性逐渐增大。

图12为根据图3整理的不同级配试样三轴试验剪胀规律。

α、β与级配参数D制样之间的关系曲线见图13，α与D制样关系仍可采用式（2）的二次函数描述，相关系数R2=0.948；由于参数β本身较小，D制样变化对于参数β的影响不明显，可取为常数0.022，相当于假定堆石料在应力比η→0时dg→∞的性质，即在研究堆石料的剪胀规律时，认为等向压缩因素受堆石料粒径分布的影响较小。

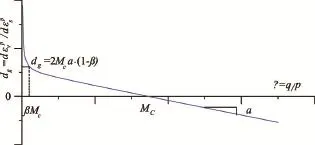
图9 模型剪胀方程的参数

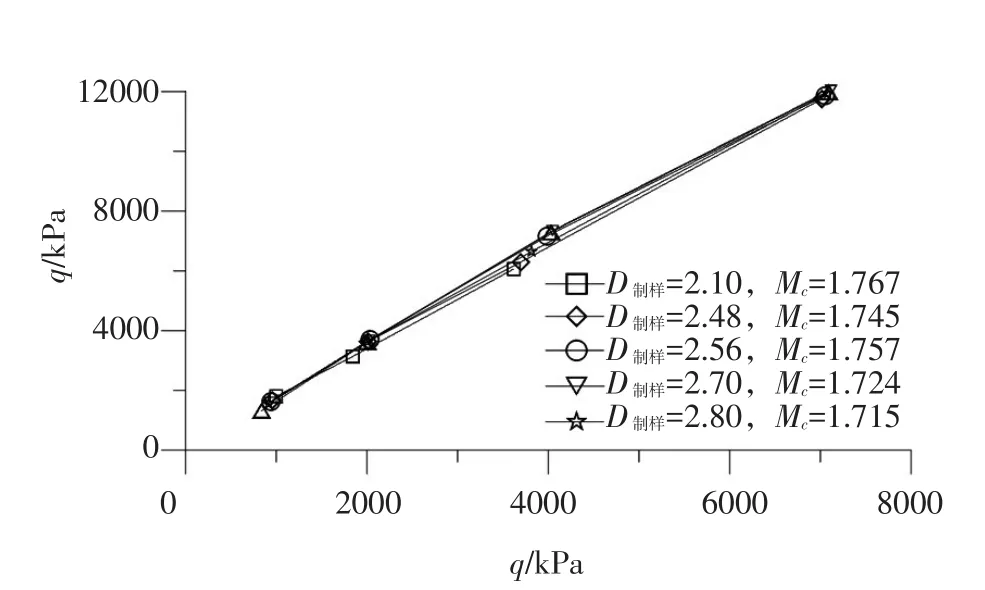
图10 试验剪胀比

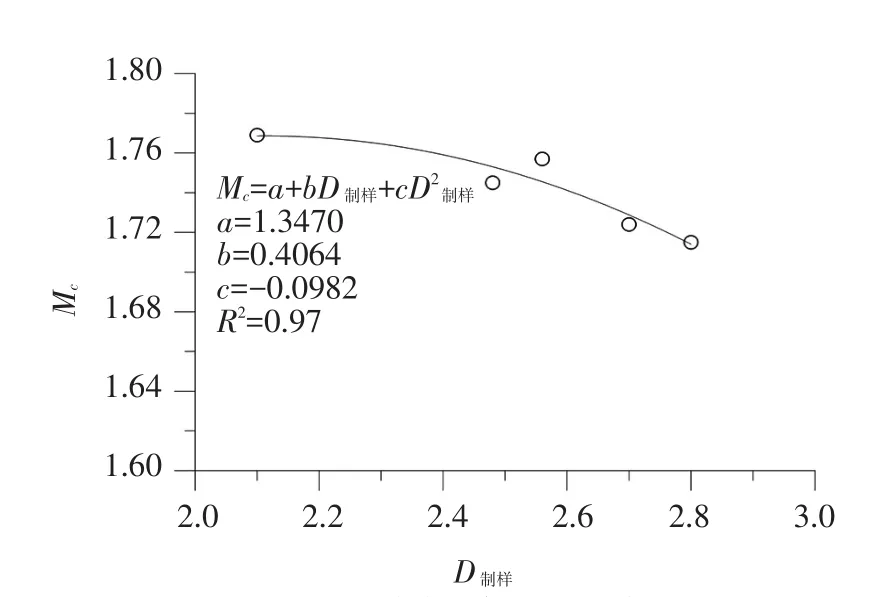
图11 剪胀比与D制样的关系

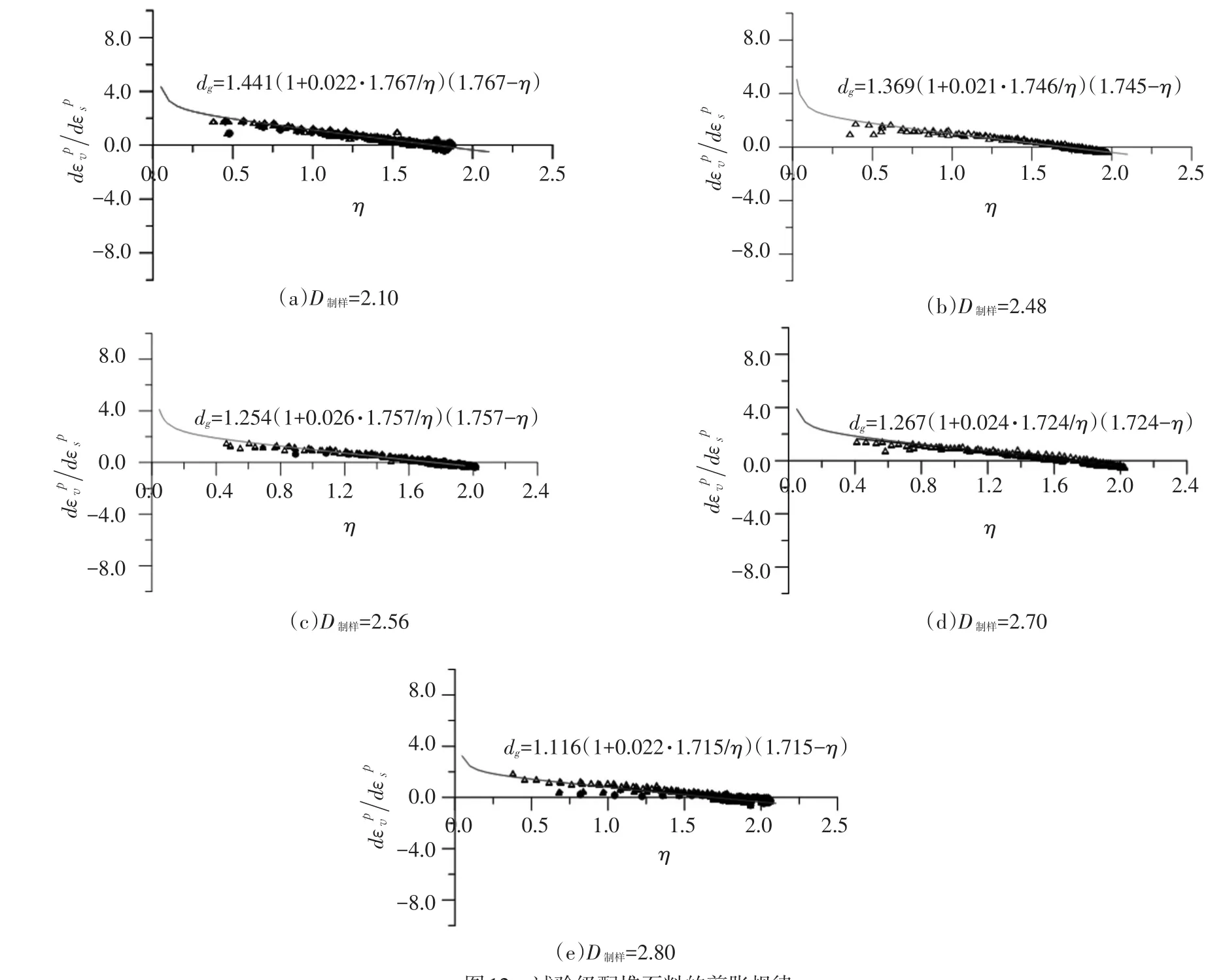
图12 试验级配堆石料的剪胀规律

3.3 压缩特性与级配的关系对于堆石料的等向压缩变形，模型［24］采用下式计算：

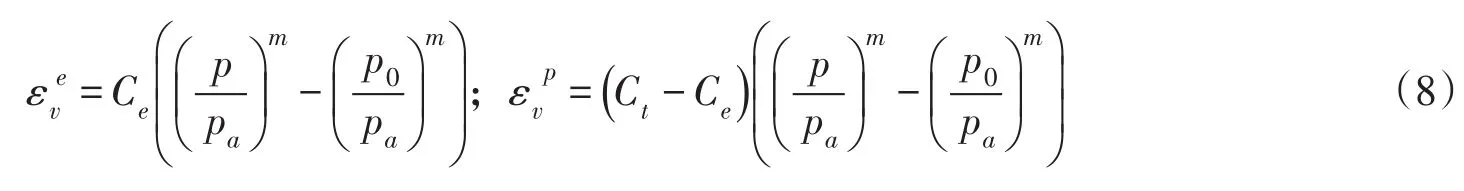
式中：为塑性体积应变；为剪切体积应变；Ct、Ce为等向压缩曲线的压缩指数和回弹指数；m是幂次，反映体变随平均应力增加而降低的程度。

由于未进行等向压缩试验，确定参数Ct、Ce、m时采用文献［23］的方法，即通过拟合三轴试验资料，采用IGA反演确定；对于堆石料的塑性模量性质参数d，也一并反演确定，得到其模型参数，见表3。

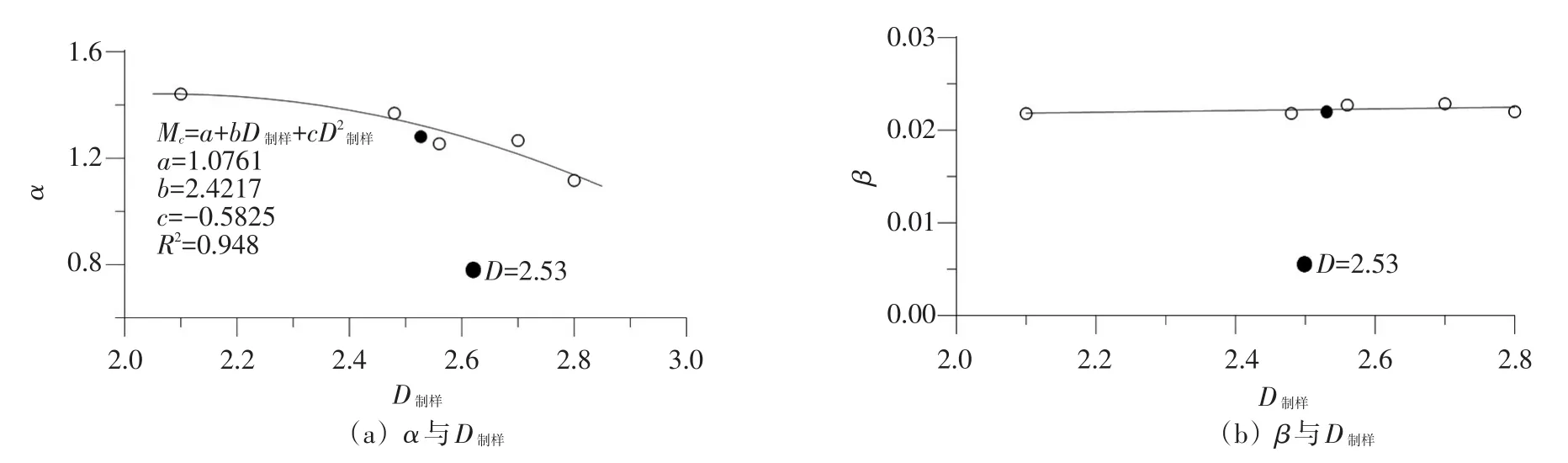
图13 剪胀参数与制样级配之间的关系

表3 不同级配堆石料的压缩参数及d值

将表3中的压缩参数Ct、Ce、m及塑性模量性质参数d与制样分形维数D制样的关系曲线绘于图14。从图14（a）（b）（c）可见，随着级配分形维数的增大，堆石料的压缩参数均出现递减趋势，宏观上解释为随着细粒含量的增加，使得堆石体内部充填更为密实，压缩变形减小，剪胀特性越来越明显。3个压缩参数与D制样的关系均可用式（2）的二次函数表示，其中，D制样在2.1～2.8之间变化时，m由0.597减小到0.525，可见D制样对m的影响幅度相对较小。

模型参数d与D制样的关系见图14（d）。由图14（d）可见，d随D制样的增加而逐渐增大，采用式（2）的二次函数模型同样可以拟合较好。

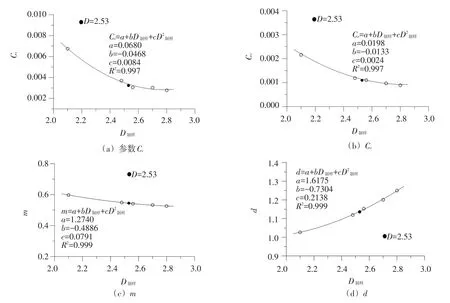
图14 压缩参数Ct、Ce、m及模型参数d与D制样之间的关系

4 模型验证

选取图3（c）所示制样分形维数2.53的三轴试验应力应变曲线，检验本文堆石料级配与模型参数相关关系的合理性。为此，分别采用上述堆石料的模型参数与D制样的关系式，计算得到模型各参数，见表4。

表4 D制样=2.53级配堆石料模型计算参数

利用表4中的模型参数，反算D制样=2.53级配堆石料在围压分别为0.4、0.8、1.6和3.1 MPa条件下的应力应变曲线，绘于图15，由图15可以看出，计算结果与试验测量值吻合较好。根据本文建立级配相关的模型参数，可以较好地预测不同级配堆石料的应力应变特性，也证明了颗粒级配是影响堆石料力学性能的主要原因。

5 结论

（1）堆石料的物理力学性质与其级配密切相关。随着粒度分形维数增大，细粒所占比重增多，堆石料的密实度、抗剪强度呈先增大后减小的趋势，制样分形维数在2.6附近最为密实，峰值强度最高。（2）建立了堆石料颗粒破碎与制样级配及围压的关系，揭示了颗粒破碎是导致高围压下抗剪强度降低的内在原因。（3）粒度分形维数的二次函数可以较好地反映堆石料级配对其物理力学性质的影响，文中所建立的级配相关堆石料广义塑性本构模型及参数，可用于考虑填筑级配影响的土工计算分析。